灰色模型在我国流脑流行预测中的应用

马 霞，高玉洁，刑青红，李冬青

(太原工业学院 理学系，山西 太原 030008)

0 引言

流行性脑脊髓膜炎(简称流脑)是由脑膜炎奈瑟菌引起的呼吸道传染病.分析流脑流行疫情动态对预测流脑流行有重要意义[1].灰色模型是利用较少的或不确切的表示灰色系统行为特征的原始数据序列生成变换后建立起来的[2].灰色系统理论以“部分信息已知，部分信息未知”的“小样本”“贫信息”不确定性系统为研究对象，主要通过对“部分”已知信息的生成、开发，提取有价值的信息实现对系统运行行为、演化规律的正确描述和有效监控[3].灰色模型在预测手足口病、肺结核、梅毒等方面已有较多的应用[4-6].

利用灰色系统理论可对被测系统的发展变化进行全面的分析观察和长期预测,近几年来该理论已广泛应用于生物医学领域，并取得了较好效果[7].本文将利用我国法定传染病报告的2011-2018年流脑年发病数据[8]，结合数据预处理的几种方法(开四次方根，取自然对数，三点数据平滑和二阶弱化算子处理)，消除数据的随机波动，建立GM(1,1)模型进行预测，从中可以看出流脑在我国未来几年的整体流行发病趋势，为流脑的防控工作提供一定的依据.

1 GM(1,1)模型的建立与计算

1.1 数据来源

2011-2018年每年流脑的发病数数据来源于疾病控制中心网站，见表1.

表1 2011-2018年流脑的发病数[8]

1.2 数据的检验

将2011-2018各年的发病人数设为原始数列，即

X(0)=(x(0)(1),x(0)(2),…x(0)(8))=(265,227,227,205,126,117,133,133)

1.3 GM(1,1)模型建立

对X(0)作一次累加，得

X(1)=(x(1)(1),x(1)(2),…,x(1)(8))=(265,492,719,924,1 050,1 167,1 300,1 433)

对X(1)作紧邻均值生成，得

于是可得矩阵

及参数列

YN=(x(0)(2),x(0)(3),…x(0)(8))T=(227,227,205,126,117,133,133)T

利用MATLAB软件计算得出：a=0.126 0,b=283.870 4.

可得GM(1,1)模型：

由于a=0.126 0，-a≤0.3，故GM(1,1)模型可用于中长期预测；

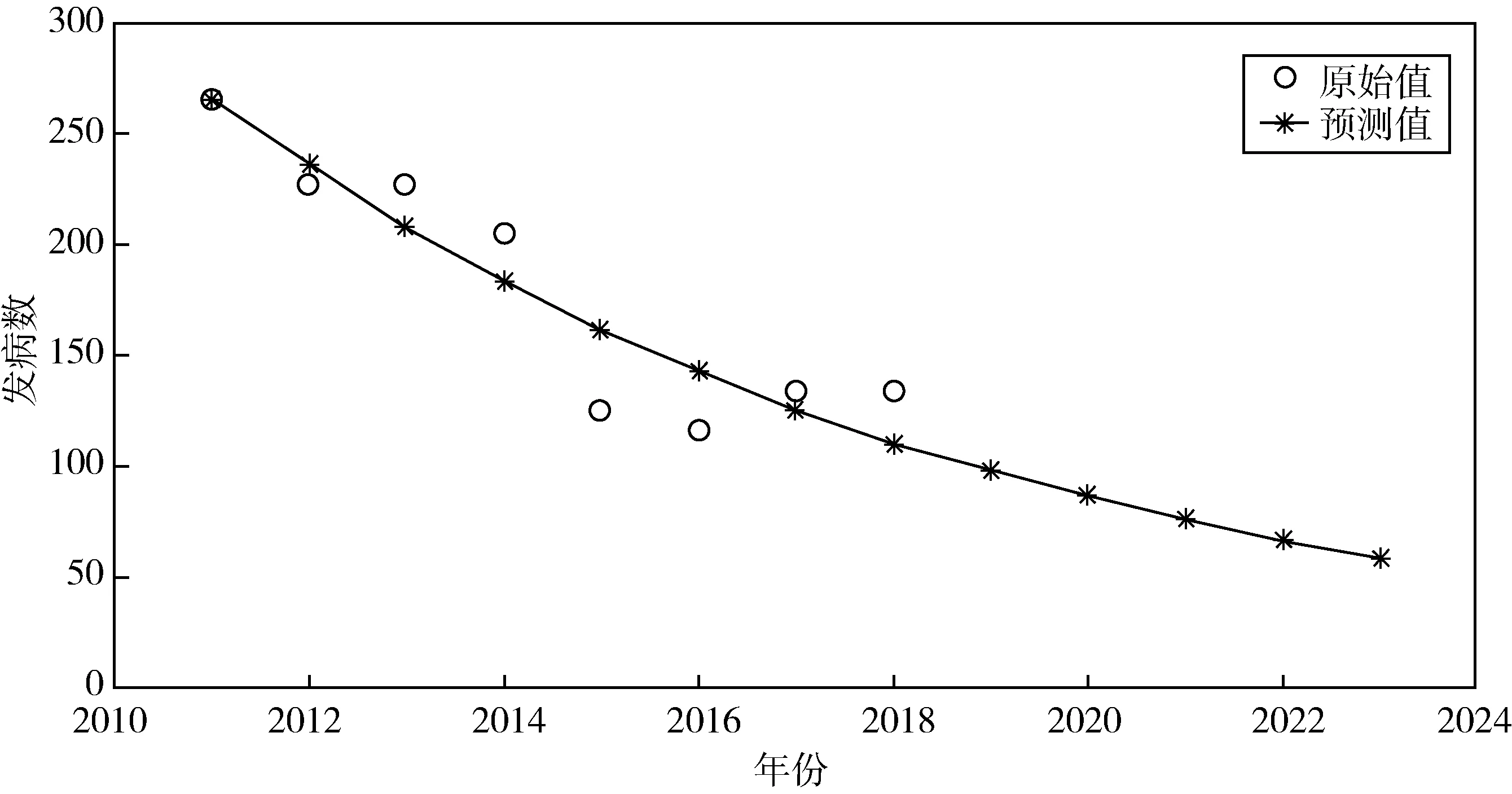
图1 模型的预测值与法定报告的流脑发病数的对比

根据建立的GM(1,1)模型，利用MATLAB求解得模型预测值以及模型的精度检验等级，见表2和3.并将模型的预测值与法定报告的流脑发病数呈现在曲线图1中进行比较.由表中数据可知，仅有小误差概率的精度为一级，均方差比的精度为二级，而模型预测值的相对误差较大，由此可见直接利用原始数据建立的灰色模型预测精度一般.因此，需要消除数据的波动变化，减少数据的随机性以及调整数据的变化态势，对原始数据进行必要的预处理，使之建立的灰色GM(1,1)模型预测精度较高.

表2 基于2011年～2018年数据模型的预测值

表3 GM(1,1)模型预测我国流脑每年发病情况的精度值

1.4 数据处理后的GM(1,1)模型建立

下面我们将采用数据开4次方，数据取对数，数据平滑和二阶弱化算子4种方法[9]对数据进行预处理，然后在建立相应的GM(1,1)模型进行预测分析.

1)数据开四次方：即对我国流脑发病人数原始数据列开四次方，参照上述建模过程可得灰色模型为：

2)取自然对数：对原始数据列取对数即对我国流脑发病人数原始数据列取对数，得GM(1,1)灰色模型为：

3)数据平滑法：预处理的数据平滑设计为三点平滑，具体按照式下式进行：

X(0)(t)=(X(0))(t-1)+2X(0)(t)+X(0)(t+1))/4

序列两端点分别按照下式处理：

X(0)(1)=(3X(0))(1)+2X(0)(2))/4,X(0)(m)=(X(0)(m-1)+3X(0)(m))/4

参照上述建模过程可得灰色模型：

4)二阶弱化算子处理：序列算子弱化处理方法是将原点数据(即最新数据)不变换，其前面的数据则按照下式进行变换：

在上式的基础上，鉴于预测精度的影响，文中对数据进行了二阶弱化算子的预处理，具体即是在上式所得数据的基础上再按照下式进行进一步的处理：

参照上述建模过程可得灰色模型为：

按照上述过程，利用MATLB软件分别计算出用自然对数、三点平滑、二阶弱化算子处理后的原始序列建立的灰色模型的精度，精度值见表4.基于2011年～2018年的流脑发病数据，将2016，2017和2018年的数据与四种数据预处理后建立的模型预测值进行相对误差对比，见表5.在对原始数据进行四次方根处理、自然对数处理和三次平滑处理所得的灰色模型预测值相对误差相差不大，精度均为二级，精度一般，预测模型的效果并不理想.而二阶弱化算子处理所得模型预测精度很好，且在近三年来，随着年份的增加，预测精度也相应提高.利用MATLAB软件计算得出四种方法预处理后的原始序列建立的模型的预测值如表6所示，并将预测值与与法定报告的流脑发病数呈现在曲线图中进行比较，如图2所示.由表6可知，利用二阶弱化算子处理原始数据得到的预测模型预测的2019-2023年的流脑发病数基本处于稳定值，从另一方面说明该病在我国的流行不会出现大范围的爆发，但也不会消失会一直持续存在.因此，我们应该做好相应的预防控制措施.

表4 我国流脑2011-2018年发病情况模型精度值(数据预处理后的GM(1,1)模型)

表5 基于2011年～2018年数据的预测模型及其相对误差比较(误差%)

表6 数据预处理建立的GM(1,1) 模型预测2019-2023年流脑的发病数

2 结语

本文以2011-2018年我国流行性脑脊髓膜炎每年的发病数为例，通过对原始数据累加以及四种数据预处理的办法，建立相应的灰色模型来预测未来几年的流脑发病数.通过比较得出采用二阶弱化算子的数据预处理方法，所得的灰色模型的预测精度较好，且在近三年来，随着年份的增加，预测精度也相应提高很多；通过模型预测得出2019-2013年流脑在我国的发病数据可知，该疾病的发病状况基本处于稳定状态，不会大范围的爆发.本文不足之处在于没有考虑可能会影响流脑发病情况的各种因素，如疫苗、温度，地区，性别、年龄等，只是在数据上进行处理，这也为未来我们的工作提供一定的建议.

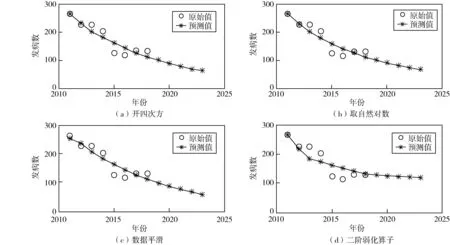
图2 我国流脑年发病数与模型预测值的拟合曲线图