一种高效的实视图选择算法
2019-10-15耿海军
张 举,耿海军
(1.山西大学 软件学院,太原 030006;2.网络与交换技术国家重点实验室,北京 100876)
0 引言
随着数据库技术的发展和完善,学校和企事业单位内部积累了大量并且复杂的数据,但是,如何有效地利用如此海量的数据成为目前研究的重点和难点.传统的数据库系统在面对这样庞大且复杂的数据时,在增删改等基本处理操作上必然会耗费大量的时间成本,将导致不能有效地利用和处理到大量数据.因而,在用户需求上传统的数据库系统的局限性日益明显,数据的处理方式及联机事务处理系统OLTP愈发满足不了人们对数据库系统的需求.越来越多的企业发现了数据库系统潜在的问题,并且希望能够对用户提交的数据进行多角度、多维度地展示和分析,从而对用户的需求有更深入地了解,尽量让自己的产品满足用户的需求,因此,如何从传统数据库中海量并且复杂的数据中获取对决策支持有用且重要的信息,已经成为现在数据库系统研究的重点和关键,在深入研究了上述问题以后,数据仓库[1]的概念被提出来了.
如今,世界上一些有名企业已经设计出了自己的数据仓库系统.例如,IBM的数据仓库产品DB2 UDB,Informix提出的IDS动态服务器,微软的OLAP服务器,Sybase的数据仓库平台Sybase IQ.相继推动了数据仓库系统的广泛发展.
随着数据库系统发展的日益加快和在各个领域的应用日益广泛,在数据库系统中存放大量的信息也是不可避免的,但其中的部分信息已经过,甚至有些数据已经没有价值,因此如何从大量并且复杂的数据库系统中寻找对用户有用的信息成为了数据库系统设计的关键.随着对该技术的深入研究,联机分析处理(OLAP)被提出来,并且OLAP的发展和数据仓库的发展互为动力,二者相互影响,相互促进,经过了数十年的发展,二者的基本模型和基本技术已经趋于成熟.
数据仓库中的一个重要问题是如何选择实视图.查询结果存储在数据仓库的实视图中,有效提高了查询响应速度.实枧图技术已在数据仓库、完整性约束、查询优化、决策支持等方面得到广泛的应用.实视图技术加快了OLAP查询响应速度,但是同时也带来了一定问题,一方面实视图在存储上需要占用一定空间[2],另一方面当基表发生改变时,对应的实视图也要发生改变.可以将部分视图作为候选,并将其实体化,这样,查询的动作就是如何选择这些实视图.
但是,一方面在数据仓库中有海量的视图,想要存储所有的视图所要花费的空间代价是不可想象的;另一方面当基本的事实表需要更新时,实视图也需要更新,视图的维护代价显然会有所增加,因此在实际应用中想要实体化所有的视图近乎是不可能的.由此可见实视图选择问题不能无限制的选择跟新,需要在一定条件的限制下,实体化一组视图,从而提高查询性能[3].
1 实视图的选择的代价模型和问题描述
1.1 实视图的选择的代价模型
作为优化数据库查询方向的关键点,实视图的选择代价模型和问题描述尤为重要,因此,数据库性能很大程度上受对于已选视图以何种方式实现物化的影响.虽然对此有着各异的尝试,但时至今日,仍未找到一种最优解,物化视图选择问题现已被证明列为:NP-Hard问题.
查询代价,维护代价,空间代价[4],这是物化视图要考虑的三个方面.
其一,物化视图技术是一种以空间换时间的技术,必须占据存储空间.过多的视图物化必定占据过多的存储空间,这一不可避免的矛盾决定了物化视图在数量上的有限性.
其二,对于物化视图原数据的变化,为保持一致,以其为基础的物化视图必须保持同步的更新,但是如果面对大数据量的复杂情况,在同步更新上的代价是不可想象的.
所以考虑到空间和维护代价等多方面因素,如何对视图进行最优物化的重要性不言而喻,其中的关键则是如何维护响应性能上的最优和最小开销之间的平衡.
图1显示了视图数量,磁盘使用空间,维护成本及维护时间的约束四者之间的关系.从图1可以看出随着实视图数量的增加,查询时间逐渐缩短,但是对使视图的维护代价和实视图占用的存储空间逐渐增加.但是科学技术在不断的革新和进步,磁盘的费用也在大幅下降,存储大量的数据成为可行条件,在存储空间上的限制不再是考虑的主要约束条件.因此,本文讨论的主要问题是,基于一定的维护成本,选择一组视图进行实现,并最小化视图的查询成本.Gupta and Mumick[5]首次提出了维护代价限制条件下的实视图选择,这个问题解决起来比起空间代价限制更加困难,因为随着选择的实视图数目的增加,维护代价可能会减少,而不是单调增加.
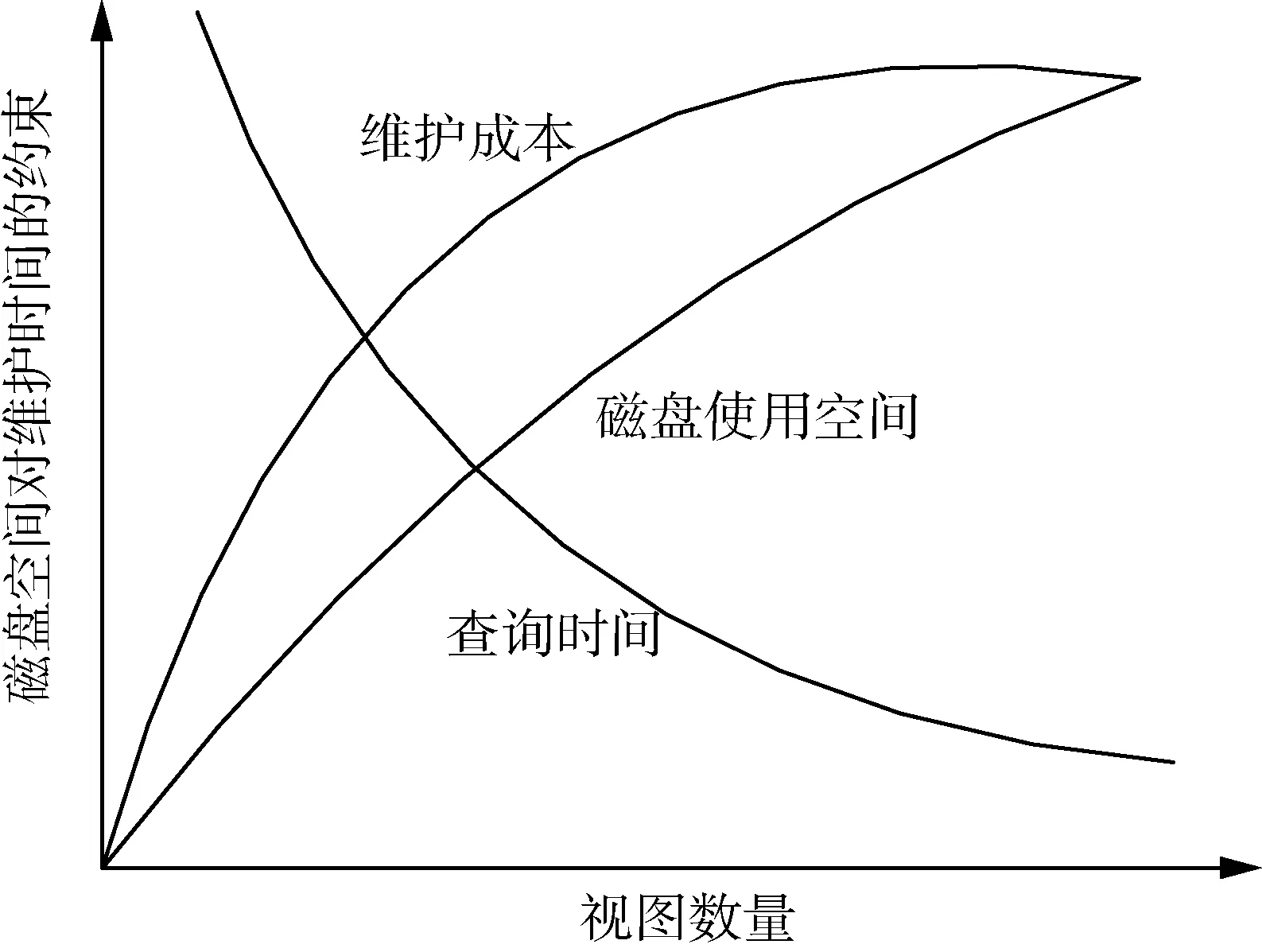
图1 物化视图数目与磁盘空间,视图维护,查询响应时间的关系图
“数据主要通过星形模型和雪花模型存储在数据仓库中. 其中,中心表和辅助表是星形模型中的主要构成”[6].前者数据量较大,但没有冗余;而后者则比较小.下面将以农产品数量安全智能分析与预警关键技术支撑系统及示范系统为例说明星型模型的存储,该系统的主题主要包括生产,价格,销售.我们以生产主题为例说明数据的存储.生产主题事实表主要是生产表p,表中主要内容为生产的数量,维表主要包括时间维度t,地点维度l,产品维度i,如果不考虑每个维度上的层次,在上面的多维数据集中用户可能有23种查询,每种查询都是针对事实表,只是group by语句不同,并且每种查询都是针对事实表进行的.假设我们要查询玉米在各个地区的产量.我们定义的SQL语句为:
Select sum(产量) from p,i where 农产品名称=”玉米” group by l ;
由上面的多维数据集构成的立方体的格如图2所示.
其中视图tli代表基表称为基本方体,任何视图都可以由它得到,all为顶点方体,表示三个维的汇总.
下面为实视图选择代价模型的一些定义:
定义1每个节点对应三个权值查询频率fv,更新频率uv,读取代价rv.每条边对应两个权值quv ,muv.其中,muv代表在视图v中对视图u的更新成本,而quv代表在视图v中查询视图u的成本.
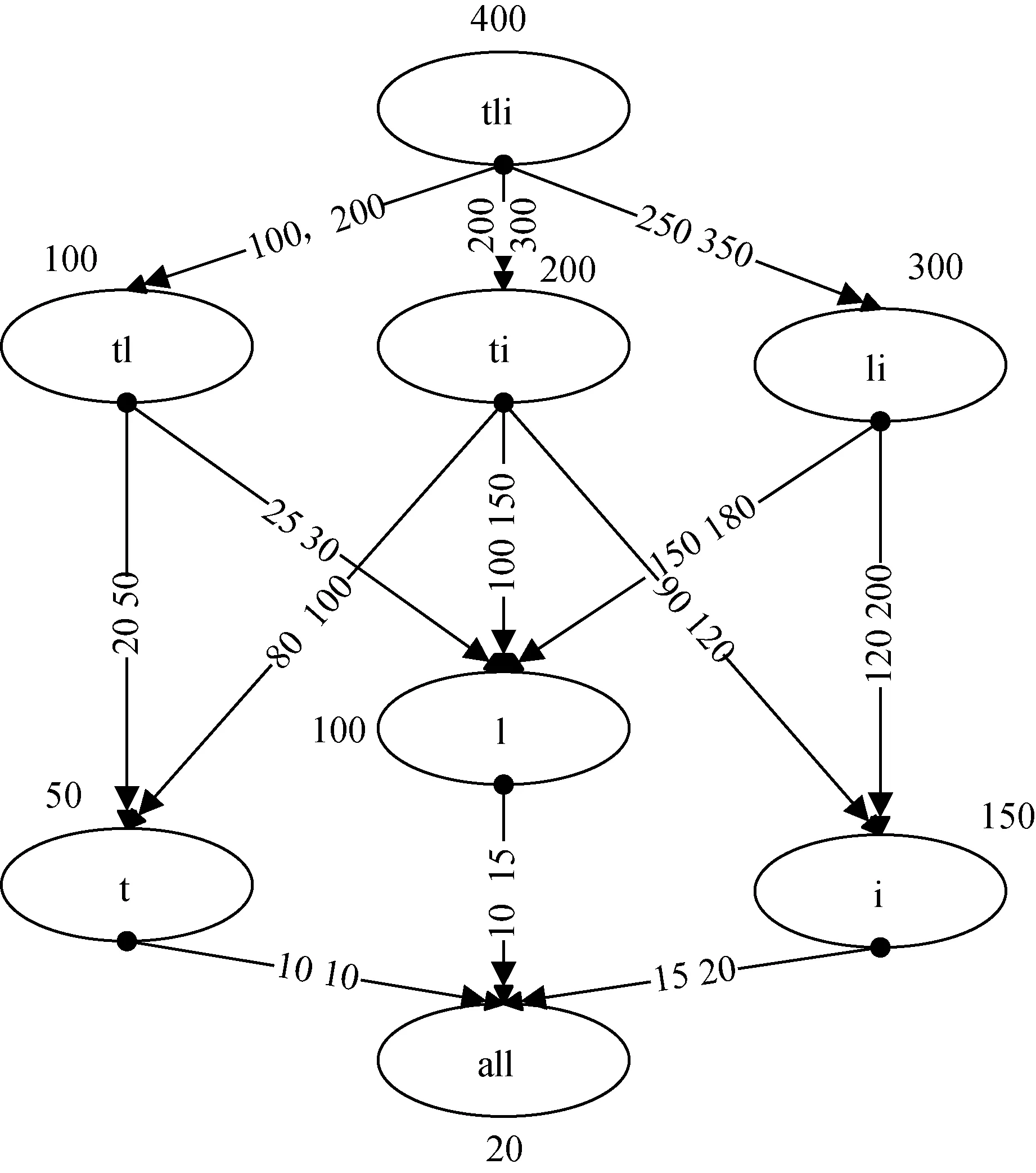
图2 数据立方体格图
定义2一个视图v的查询成本q(v,M),等于利用M去查询视图v的最小查询成本,其中,M为数据仓库中的物化视图集.即:
q(v,M)=min{q(v,vm),vm∈M}.
(1)
定义3当视图集M被物化后,视图v的查询频率为fv,则总查询代价等于V(G)中每个视图的查询代价的加权和.
(2)
定义4一个视图v的维护成本m(v,M) ,等于从物化视图集M去更新视图v的最小维护成本.即:
m(v,M)=min{m(v,vm),vm∈M}.
(3)
定义5当视图集M被物化后,视图v的更新频率为gv,则总的维护成本如下:
(4)
以图2中的数据为例说明上述定义:
q(t,M)=100+20=120
q(l,M)=100+25=125
q(all,M)=min(100+10+10,100+25+10)=120
u(tl,M)=100
AssumeQ(tli)=100U(tli)=100
q(tl,tli)=400+100=500
q(t,tli)=min(400+100+20,400+200+80)=520
q(l,tli)=min(400+100+25,400+200+100)=525
q(all,tli)=min(400+100+20+10,400+100+25+10,400+200+100+10,400+200+80+10,400+200+90+15,400+250+50+10,400+250+120+15)=530
1.2 问题描述
本文需要的解决的问题可以描述为:
minQ
s.t.
U≤Ω,其中Ω为维护代价约束.
即总维护成本在不超出限定的维护成本的前提下,选择出一组被实体化的视图.
2 实视图选择
遗传过程是遗传算法的核心,它有优胜劣汰、交叉遗传、小概率变异等优势,进而可以有效的维护种群的多样性、稳定性,保证优胜劣汰.过程如下:
1)遗传编码:在具体算法中,将视图用0和1编码表示,其中1代表该视图已被实体化,而0则相反.这样,向量(0 1 0 1 0 0 1)就代表第二,第四及第七视图已被实体化.
2)初始种群的生成:先后使用深度优先和随机的方法生成.
3)选择算子:采用轮盘赌选择策略.
4)交叉算子:对选择的种群之间随机相互交叉匹配,产生子代种群.
为保护最优解并加快劣质解的淘汰速度,本文采用Srinivas提出的自适应遗传算法(AGA)[7]中可根据适应度的变化而变化的交叉概率Pc.
交叉概率Pc的计算公式为:
(5)
其中,k1,k2为常数且小于1,f代表种群适应度,f'代表两个中的较大者.
5)变异算子:此处采用Srinivas提出的自适应遗传算法(AGA)[7]中的变异概率Pm.变异概率Pm的计算公式为:
(6)
其中,各符号意义同公式(5).
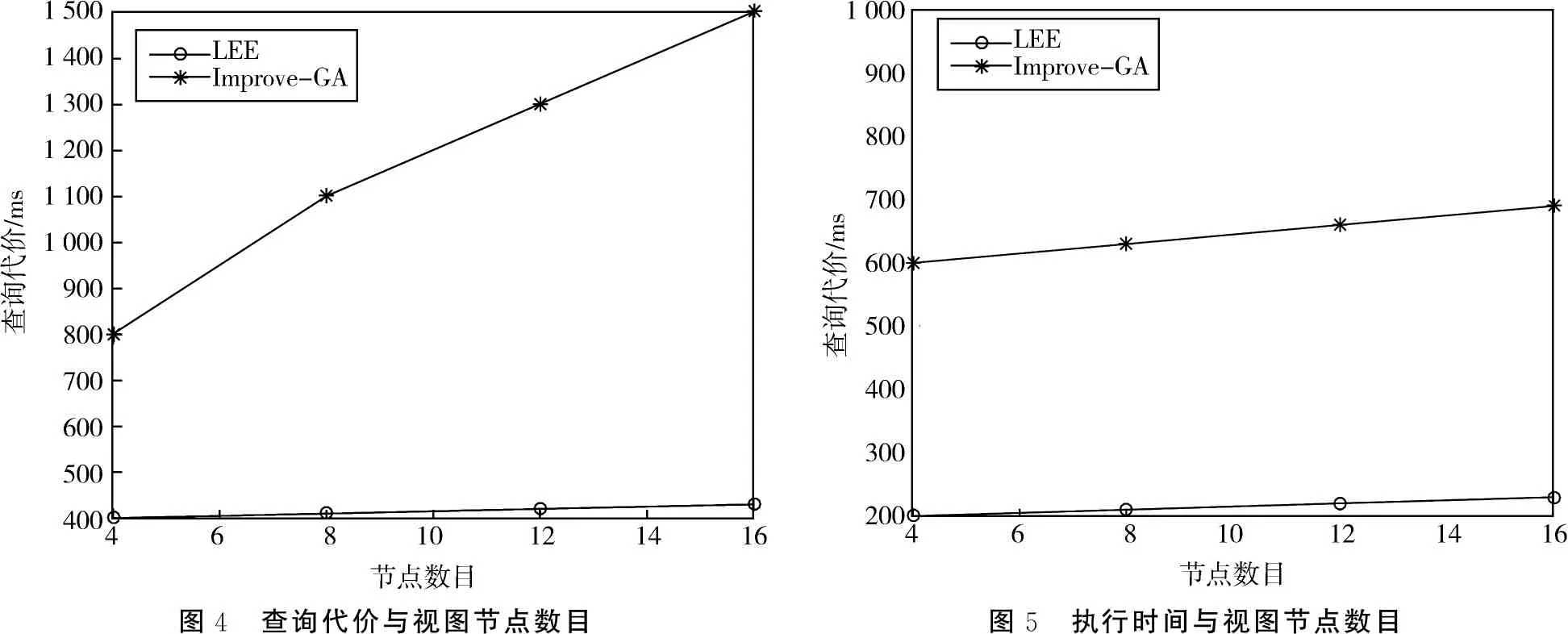
从已有的关于遗传算法的文献中我们得知,若要保证遗传算法的性能保持在一个较高的水平,Pc和Pm需要保持在0.5 6)适应度函数:适应度函数主要用于评估个体的优越性和劣势. 其值如果较大则表示个体具有更大的生存机会,相反则该个体更容易消亡.对于我们的问题,必须考虑查询收益和维护代价的限制,但是维护代价的限制比起空间代价的限制复杂得多,这是因为当一个视图被实体化后,它的维护代价不仅取决于它自身而且取决于其他的物化视图.解决此类复杂问题的较好方法是在适应度函数中引入惩罚函数,当维护代价满足条件时,惩罚函数不会起任何作用,当维护代价不满足条件时,惩罚函数将会降低适应度函数的值.当引入惩罚函数后,维护代价将不再是限制条件.Lee and Hammer在[8]中提出了维护代价限制条件下利用静态惩罚算子构造的惩罚函数来解决实视图选择(我们将其算法简称为LEE算法).但是静态算子的选择对结果的影响比较大,不容易确定.因此我们利用Vassilios Petridis提出的动态惩罚函数[9]来解决视图选择问题. p=a(g)*d(s)+b(g). (7) (8) (9) d(s)=max{U(M)-E,0}. (10) 其中G为最大遗传代数,g为当前遗传代数,A,B是惩罚因子,并且A,B应尽量大,这样可以很容易区分出有效解和无效解.因此适应度函数为: f(x)=Q(φ)-Q(M)+p*v. (11) 当为有效解时v=0,反之v=1. Improve-GA算法代码如下: Begin 随机产生初始种群G(0); t=0; repeat 用适应性函数评估G(t)中的每个个体; t=t+1; while G(t)<=population_size { 从G(t-1)中选择两个个体; 按照交叉概率Pc执行杂交(crossover)操作; 按照交叉概率Pm执行变异(mutation)操作; 将结果赋给G(t); } until t <=max_gen; End 杂交操作的代码如下: 输入:种群G Begin 随机选择在种群G中的两个个体g1(u1,u2,u3,…,un),g2(v1,v2,v3,…,vn); 根据上述公式计算Pc; 产生一个范围在0-1之间的随机数c; 产生一个范围在0-n之间的随机数number; If(c For(int j=number;j<=n;j++) { t=g1(xj); g1(xj)=g2(yj); g2(yj)=t; } g1’=g1; g2’=g2; End 变异操作的代码如下: 输入:种群G begin for every individual in do for every bit in the individual do Mutate the bit with the probability pm; end for 图3 查询代价和维护代价之间的关系 end for end 本文进行了一系列的模拟实验.实验环境用的操作系统为Windows 10,编程语言使用C++,所用的数据库为SQL Server 2017. 对维护成本为0.5 Umin- Umin的条件下(Umin为当所有视图都被实体化后的最小维护成本),对LEE和Improve-GA两种算法的查询成本进行了对比,如图3所示.从图中可以看出,当维护成本较小时,LEE和Improve-GA在性能上差距很小,但是随着维护成本的增加,Improve-GA表现出了更好的性能. 实视图选择算法会随着节点数目的增加其性能会大大降低,因此我们比较了当节点数目增加时Improve-GA算法和LEE算法对应的性能. 当限定维护代价为0.7Umin时,查询代价随节点数目变化的关系如图4所示.从图4可以看出,当节点数目在4-16变化时,随着结点数目的增加Improve-GA的查询代价较小. 图4 查询代价与视图节点数目图5 执行时间与视图节点数目 当限定维护代价为Umin时,查询代价随节点数目变化的关系如图5所示.从图5可知,查询代价的执行时间基本曾线性变化,Improve-GA算法的执行时间较短.由图4和图5可以得出结论如下:随着节点数目的增加LEE算法的性能越来越差,而Improve-GA算法性能比较优越,从而说明Improve-GA算法的使用范围更广. 选择视图实体化算法是数据仓库中的研究热点之一.在这个过程中,有些算法侧重于对视图存储空间影响的研究,但随着存储技术及相关硬件产品成本的降低,这一影响因素的重要性已经下降了.因此,本文提出以成本一定为前提,选择一组使查询成本最小的视图实体化.通过实验比较了Improve-GA算法和LEE算法,从而证明了算法的可行性和有效性.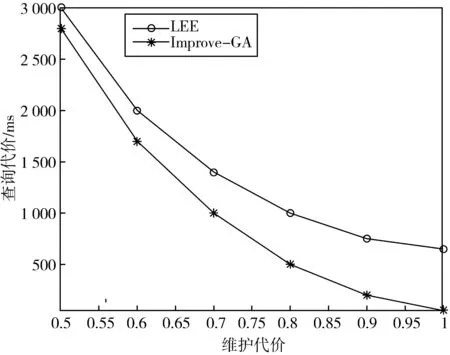
3 实验研究
4 结语
