涡流发生器对风力机翼型气动特性的影响研究
2019-10-15
(1.西安理工大学,陕西 西安 710048; 2.中国质量认证中心,北京 100070;3.北京金风科创风电设备有限公司,北京 100176)
0 引言
随着风力发电机组向大功率机组的发展,叶片长度被设计的越来越长,为了保证风力机叶片的强度要求,大型风力机翼型从中部到根部一般都采用加厚的风力机专用翼型,但在大攻角下,厚翼型很容易发生流动分离,导致叶片吸收风能的效率降低。通常在叶片上添加附加装置进行流动控制以减小或延缓流动分离,达到提高叶片气动性能的目的。涡流发生器(VGs)是一种基于控制边界层分离的增升减阻技术[1]。VGs不需要改变叶片原构型,以其最有效与实用以及性价比最高的边界层分离控制技术成为近几年边界层分离控制研究的热点。
涡流发生器技术最早由美国联合飞机公司的Bmynes和Taylor等在1947年提出[2]并首次用于机翼上。VGs一方面是通过小平板产生的尾涡搅动分离区内的气流,使边界层上部的高能气流得以与近壁的低能气流混合而增加近壁流体的动量和能量,从而延缓分离;另一方面是利用涡流发生器产生的尾涡阻隔向外翼的流动,防止低能气流在外翼上堆积,从而进一步增加升力和减少阻力[3-4]。经过逐步发展,涡流发生器已被广泛用于大型风力机上,国内外很多学者应用实验或者数值仿真的方式对此进行了研究。1986年,J D Nickerson Jr用实验的方法研究了低雷诺数下,VGs对大型风力机叶片厚翼型NACA0024升阻特性的影响[5],得到了VGs能通过提高翼型的升力系数提高升阻比的结论。2004年,Jeppe Johansen等指出三角形涡流发生器可以显著推迟叶片失速分离,提高气动性能[6]。2005年,Johansen等在数值计算中采用半对VGs,设置VGs两侧为对称和周期性条件,来研究VGs对风力机叶片气动影响规律[7]。国内,刘刚等人研究了模拟VGs的数值计算方法,分析了VGs的安装方式、剖面结构及几何尺寸等因素对机翼气动分离的影响规律,阐述了VGs对超临界机翼的气动影响[3]。
国内外针对涡流发生器对翼型气动性能影响的文献较多,多基于航空翼型。且对于涡流发生器对风力机专用翼型气动特性影响的实验研究国内相对较少,国外的相关实验数据很少公开。
涡流发生器控制流动分离的效果与其自身形状参数、弦向位置参数、涡流发生器对之间的水平安装间距、安装角等都有关系,本文研究对象为NACA63-415翼型,研究三角形VGs长度、高度、弦向安装位置及与来流方向夹角对翼型气动性能的影响。
1 数值模拟方法
1.1 控制方程
本文计算所采用的计算软件FLUENT为目前功能最全面、适用性最广、国内使用最广泛的CFD软件之一。本文计算采用的版本是FLUENT 14.5。
本文计算湍流的模型采用基于压力基的Realizablek-ε(RKE)模型,该模型的优点是对旋转、有大反压力梯度的边界层、分离、回流等现象有很好的预测结果。
可实现k-ε模型的湍动能及其耗散率输运方程为
(1)
(2)
其中
η=Sk/ε
式中Gk——由平均速度梯度引起的湍动能产生;
Gb——用于浮力影响引起的湍动能产生;
YM——可压速湍流脉动膨胀对总的耗散率的影响;
C2和C1ε——常数;
σk,σε——湍动能及其耗散率的特普朗特数。在FLUENT中,作为默认值常数,C1ε取1.44,C2取1.9,σk取1.2,σε取1.0。
可实现k-ε模型的湍动能的输运方程与标准k-ε模型和重整化k-ε模型有相同的形式,只是模型参数不同,但耗散率方程有较大不同。首先耗散率产生项(方程右边第二项)不包含湍动能产生项,文中的形式更能体现能量在谱空间的传输。另外的特色在于耗散率减少项中,不具有奇异性,并不像标准k-ε模型那样把K放在分母上。
该模型适合的流动类型比较广泛,包括有旋均匀剪切流,自由流(射流和混合层),腔道流动和边界层流动,对以上流动过程模拟结果都比标准k-ε模型的结果好,特别是可实现k-ε模型对圆口射流和平板射流模拟中,能给出较好的射流扩张角。
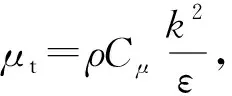
(3)
以上公式表明Cμ是平均应变率与旋度的函数。在平衡边界层惯性底层,可以得到Cμ=0.09,与标准k-ε模型中采用底常数一样。
1.2 几何模型及网格划分
本文计算采用了NASA 63-415翼型[6]。翼型宽度为350 mm,翼型弦长600 mm。Clean翼型(即未加涡流发生器的翼型)的三维图如图1所示,带有涡流发生器的翼型表面如图2所示。
本文采用前处理软件ICEM CFD进行网格划分。由于流场的入口的条件采用Pressure-far-field压力远场入口条件,因此需要一个远离翼型的边界,原则上讲,边界离翼型壁面越远越好,边界离壁面越远,边界对流动的影响越小,计算也就越精确,当然相应的计算量也相应越大,在本文中边界取翼型的弦长的10倍。流场尺寸图如图3所示。
本文采用前处理软件ICEM CFD进行网格划分。流场网格采用结构化网格进行划分,高质量的结构化网格,可以使计算结果更加准确和精确。Clean翼型流场的网格数量为97.4万,节点数为93.8万。带涡流发生器的整个模型的网格数量在800万左右。
网格划分中,在翼型近壁面处,湍流边界层很薄,求解变量的梯度很大,但精确计算边界层对翼型升阻力的计算值来说非常重要,应使用加密的网格来解析边界层,但这对工程应用来说,代价很大,本文我们采用了标准壁面函数来解决这个问题,但是标准壁面函数要求y+值应介于30到300~500之间,且网格尺度递增系数应不大于1.2。近壁面网格尺寸预估,壁面到第一层流体中心点的距离(Δy)可以通过估计壁面剪切层的雷诺数来预估,计算公式为
(4)
其中:雷诺数取1.6E+06,L取弦长0.6 m,计算得出壁面到第一层流体中心点的距离(▽y)约为0.27 mm。流场的尺寸近翼型表面采用了0.27 mm的尺寸,增长比例为1.1。Clean翼型的流场网格划分如图4、图5所示。
在建立涡流发生器的模型时做了一些简化,由于涡流发生器的厚度仅为0.2 mm,划分网格时将涡流发生器简化成无厚度的面,这样做不仅可以降低后期网格划分的难度,也有利于提高计算网格的质量。为了更好模拟各对涡流发生器之间的流场影响,该模型中包含了5对涡流发生器。涡流发生器周围的流场网格如图6所示,因为涡流发生器为三角形,因此采用Y形网格对涡流发生器表面进行网格划分,如图7所示。
1.3 边界条件及物理条件
流场的入口区域设置为Pressure-far-field压力远场边界条件,其中马赫数设置为0.112,相对应的雷诺数为1.6E+10,入口压力和温度的计算公式如下
(5)
式中p0=101 325pa,γ=1.4(对于空气)
M=0.112(马赫数)
由以上公式可得p(静压)=99 781.5pa
(6)
式中T0=300k,γ=1.4(对于空气)
M=0.112(马赫数)
由以上公式可得T=299.3K
流场入口设置为压力出口边界条件,两侧设置为对称边界条件,翼型表面设置为壁面边界条件,运行压力设置为0 Pa。
计算介质采用理想气体Ideal-gas,粘性选择Sutherland Law。Fluent计算采用双精度,控制方程的差分格式都采用二阶迎风格式。
3 计算结果及分析
3.1 涡流发生器运行参数
目前多数机组采用变速变桨控制策略,在额定风速以下通过改变风机的转速,使叶片始终工作在最大Cp点附近,此时叶片的每个截面根据叶素动量理论都工作在最佳攻角下,但在叶片根部和叶片尖部还是会存在边界层分离的现象,随着叶片长度的增加,这种现象会越来越严重.
为了分析涡流发生器工作的环境参数,本文使用GH bladed软件对长为45.3 m某型号叶片的气动性能进行了计算,计算结果如图8、图9所示。
图8为不同叶片截面处翼型攻角随风速的变化趋势,从图8数据可以看出在叶片根部,随着风速的增加叶片的攻角增加很快,在到达额定风速时攻角达到37.762 3°,而超过一定攻角时叶片表面易发生流动分离,图9为不同叶片截面处翼型雷诺数随风速的变化趋势,从图中可以看出,叶尖部位在额定风速时雷诺数为9.85E+06,在雷诺数过大时也会造成边界层速度递增,加速边界层的分离。
3.2 数值验证
本文采用Realizablek-ε(RKE)模型对Clean翼型,即不带涡流发生器的翼型进行数值模拟,得到其在0~20°攻角下翼型升力系数Cl和阻力系数Cd随攻角α的变化曲线, 数值模拟结果与实验结果[8]进行比较,如图10、图11所示。NACA 63-415翼型仿真和实验的最大升力系数和最小阻力系数值见表1。
表1 NACA63-415最大升力系数和最小阻力系数

实验值计算值Clmax-Clean1.331.550 8Cdmax-Clean0.0170.102
从图10、图11可以看出,NACA 63-415的升阻力系数的值与实验数据存在一定偏差,在文献[6]中,计算数据的值亦稍大于实验数据,但升力系数曲线和阻力系数曲线的变化趋势和实验数据基本一致,因此可以验证该计算方法和物理模型可以有效用于本文的数值模拟研究。
3.3 涡流发生器模拟计算
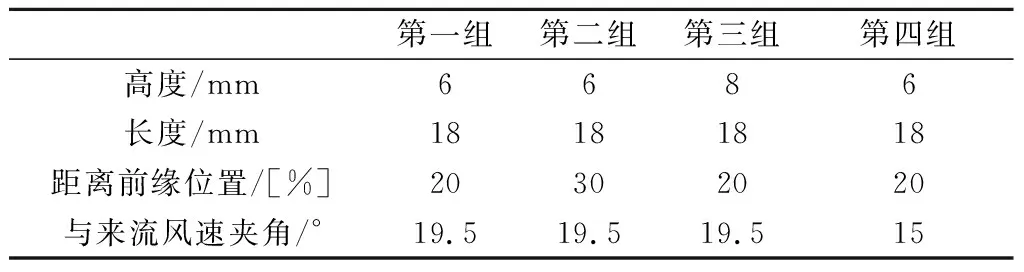
为了验证涡流发生器输入参数对翼型气动性能的影响,本文共仿真了四组模型,分别改变涡流发生器的高度、长度、安装位置距前缘位置和与来流风速夹角来模拟其气动特性,四组涡流发生器模型的数据如表2所示。
表2涡流发生器输入参数
第一组第二组第三组第四组高度/mm6686长度/mm18181818距离前缘位置/[%]20302020与来流风速夹角/°19.519.519.515
3.3.1 加装涡流发生器后翼型表面Cp值
翼型上下表面的压力分布会影响翼型的升阻比大小,翼型压力面压力越大,吸力面压力越小,翼型的升阻比越大。本文只给出第一组VG模型在攻角0~20°下,翼型表面压力系数Cp值,如图12~图16,从以下图可以看出,在安装了涡流发生器的吸力面,压力系数Cp值有明显的阶跃,且随着攻角增大,最大压力系数不断增大,翼型上下压差先增大后减小,且随着攻角的增大升阻比先增大后减小。其他组Cp值类似,本文不再赘述。
3.3.2 涡流发生器对流动分离的抑制
图17、图18、图19分别为涡流发生器尾端的涡流速度矢量图、流过翼型表面的流线图及迹线图。图17中显示涡流发生器的尾部有涡的存在,涡流发生器的布置与流动方向有一定夹角,会对左右两侧流体产生排挤或扩导的作用,受排挤的一侧流体上卷形成上洗区,受扩导的一侧流体下移形成下洗区,上洗与下洗共同作用形成了一个诱导涡[9]。在诱导涡的作用下,边界层内的低速流体与主流的高速流体进行了能量交换,从而具备了在逆压梯度下更强的抗分离能力。从图18可以清楚的看到流体在经过涡流发生器后,漩涡带动附壁面底层低能量区和高能量的能量交换。图19为流经翼面流体的迹线图。
为了更加清晰地显示涡流发生器对翼型表面流动分离的抑制作用,截取攻角15°时未加装涡流发生器翼型与加装了涡流发生器后翼型周围流场速度云图,如图20与图21,对比没有涡流发生器的云图,图21中我们可以清楚地看到涡流发生器对流动分离的抑制与延迟作用,说明涡流发生器可以有效延迟边界层的流动分离。
3.3.3 涡流发生器参数对翼型气动特性的影响
从仿真结果可以看出,在安装涡流发生器后,四组不同参数涡流发生器对NACA 63-415的升力系数均有明显的提升,升力系数开始下降的点即失速点均后移,各组翼型的升阻力系数如图22~图25所示。表3给出各组涡流发生器翼型的最大升力系数和最小阻力系数。
表3 NACA63-415最大升力系数和最小阻力系数

ClmaxCdminClean1.550 80.010 2VG11.760 10.016 161VG21.729 80.014 394VG31.724 80.015 078VG41.695 20.014 396
图25可以更清楚地比较四组涡流发生器的性能,由表3可知,安装涡流发生器后,翼型的气动性能均得到了提升,其中VG1组涡流图26可以更清楚地比较四组涡流发生器的性能,由表3可知,安装涡流发生器后,翼型的气动性能均得到了提升,其中VG1组涡流发生器对于NACA 63-415翼型升力系数的提升最为明显,翼型气动性能最佳,与Clean翼型相比较最大升力系数提升了13.5%,但阻力系数却降低了8%。
4 结论
本文以NACA63-415为研究对象,采用CFD数值模拟的方法,研究分析了涡流发生器对风力机翼型气动性能的提升作用,并在不同的涡流发生器设计参数下研究涡流发生器不同高度、长度、不同安装位置、安装角对翼型气动性能的影响作用,得出如下结论:
(1)在0~15°攻角下,验证NACA63-415 Clean翼型实例计算结果与实验结果数值吻合较好,其中高质量的六面体结构网格和正确的y+值保证了仿真结果的正确性,证明本文所采用的计算方法和Realizablek-ε(RKE)模型可有效地进行翼型的气动特性的数值模拟。
(2)通过对涡流发生器的数值模拟计算,可以看出在每对涡流发生器后部都产生了对称的漩涡,仿真结果和涡流发生器的工作原理基本一致。比较同攻角下的光滑翼型和安装了涡流发生器的翼型,可以看出带有涡流发生器的翼型翼面边界层分离点明显延后。
(3)本文针对三角形涡流发生器的高度、宽度、距翼型前缘的位置、与来流风速的夹角三个输入参数设计了四组模型,通过对不同参数的涡流发生器的数值模拟计算,结果表明,四组不同参数的涡流发生器均对提升翼型升力系数有着显著作用,其中,第一组涡流发生器,即高度为6 mm,长度为18 mm,距前缘20%弦长,与来流夹角19.5°时,对翼型气动性能的提升效果最好,证明涡流发生器在叶片气动提升方面有着一定的实际意义。
(4)本文对风力机叶片翼型气动性能的提升有一定的参考意义,由于篇幅限制,本文只进行了相对较少的涡流发生器组参数的模拟,后续可以对不同参数的矩形、梯形等涡流发生器进行模拟,寻找更优的涡流发生器参数以最大限度提高翼型气动性能;再者,本文只计算了直叶片、非旋转状态下涡流发生器对叶片气动特性的影响,后续工作可以进行旋转状态,实际叶片含涡流发生器的数值模拟,更加真实的仿真实际现场叶片工作状态下涡流发生器对叶片气动性能的影响。
