一种基于DWT_DCT 的数字图像盲水印算法

张帅，杨雪霞

（1.太原广播电视大学教学研究中心，太原 030024；2.太原科技大学应用科学学院，太原 030024）

0 引言

网络改变了大众的生活方式，数字产品也为我们带来了诸多便捷，然而非法的篡改、获取以及恶意破坏已经对数字产品造成了严重的威胁。水印技术是指在数字产品中嵌入版权所有者的身份信息，当需要认证时可通过提取水印达到版权保护的目的，也可对网络传播的数字产品进行有效的跟踪。

在数字水印技术中，离散小波变换（DWT）和离散余弦变换（DCT）得到了广泛的应用和研究。张勤等人[1]在小波变换域内分别在高、低频中嵌入了两种水印，该水印算法表现出较强的鲁棒性，但不能抵抗旋转攻击。陈小娥[2]提出了结合QR 码的DCT 水印算法，该算法可以有效提取嵌入的水印信息，但提取水印的归一化值普遍在0.9 以下，效果并不理想。徐江峰等人[3]提出了一种QR 码与DWT 和DCT 相融合的水印算法，该算法具有较强的鲁棒性，但水印信息未进行置乱处理，因此抵抗剪切攻击方面表现不足。杨剑等人[4]提出了一种分块的DCT 与DWT 相结合的水印算法，该算法分别在DWT 和DCT 中嵌入两种水印信息，实现了脆弱性和鲁棒性的双重功能，但属于非盲水印算法。

本文提出了DWT 和DCT 相融合的盲水印算法，考虑到小波变换和离散余弦变换的低频子带和低频系数中都包含了图像主要信息，在面对攻击时具有很好的稳定性。因此首先对载体图像进行DWT 变换，再对分解的低频子带进行DCT 变换。水印信息则分别通过Arnold 置乱与混沌加密预处理，并通过生成两组随机矩阵，将加密的水印信息嵌入到DCT 的低频系数中。此时经过双重加密的水印信息具备了更高的安全性，同时载体图像中的水印信息也具有更强的鲁棒性。最后通过与随机矩阵的相关性分析实现了水印信息的盲提取。

1 算法理论

1.1 离散小波变换

离散小波变换（DWT）的多分辨率特性与人类视觉特性（HVS）相似，即人类的视觉对低频信息变化较为灵敏，而对纹理、边缘轮廓则不敏感。因此对载体图像进行小波变换，结合HVS 特性，保证了嵌入水印在压缩、噪声等攻击方面的鲁棒性。离散小波变换将载体图像分为LL、LH、HL 和HH 四个子带[5]。其中LL 子带为低通滤波后的系数，代表图像的细节信息，其余子带分别代表图像的边缘、轮廓信息。本文首先对载体图像进行了一级小波分解，具体结果如图1 所示。

图1 原始载体图像与一级小波分解图像

1.2 离散余弦变换

离散余弦变换（DCT）将信号从时域转换到频域，在频域中的直流分量和低频系数中包含了图像的主要信息，因此在低频中选择合适的系数嵌入水印可以保证嵌入水印图像在滤波、不可感知性方面表现出较好的特性[6]。

本文在小波变换的基础上，为了降低DCT 计算的复杂度，对低频子带进行了分块处理，并且为了准确选择嵌入位置，我们对DCT 的系数按照Zig-Zag 进行排序。图2（a）为LL 子带的第一个8×8 子块进行DCT 变换后的系数，系数值分布较为分散，规律性较差，图2（b）我们进行了重新排序，系数分布符合Zig-Zag 特点[7]，此时我们可以根据DCT 系数的大小确定嵌入水印的准确位置。

图2 DCT系数重新排列图

1.3 Arnold变换与混沌加密

Arnold 变换是通过对图像像素值进行位置变换达到加密的目的，具体的变换公式如下：

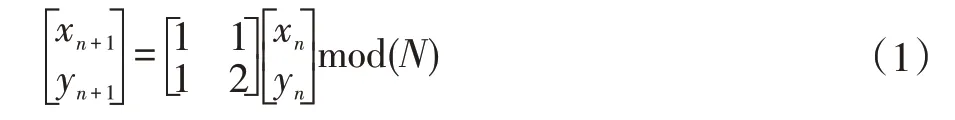
根据公式（1）对变换矩阵求其逆矩阵，得到了Arnold 逆变换公式[8]，如公式（2）所示。这样我们不必计算图像的周期性，只需根据置乱的次数，就可以将图像还原。

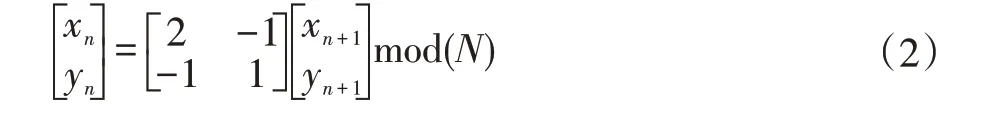
考虑到Arnold 置乱的周期性，图像经过一定次数的置乱，便可以还原为原始图像，为了提高算法的安全性，我们对置乱后的图像再次进行混沌加密，混沌迭代方程[9]如下：

其中xn为初始值，当M 接近4 时，N 为2.5 时，数列[ xn] 发散，呈现混沌状态。

本实验的水印图像迭代次数选择19，混沌加密的初始值选择2，作为本算法的加密密钥。具体实验结果如图3 所示。

图3 水印预处理过程

2 算法设计

本文选择大小为512×512 的Lena 图像作为载体图像，选择32×32 的“开”字作为水印信息，首先对载体图像进行一级小波变换，并对分解的LL 子带进行8×8 分块处理，此时LL 子带被分解为块。利用MATLAB 环境生成两个八位的随机矩阵d1和d2，并在DCT 系数中相应的选择八位低频系数作为水印的嵌入位置，本文通过大量实验，选择了Zig-Zag排序后的7 到15 位，并根据如下规则嵌入水印信息：

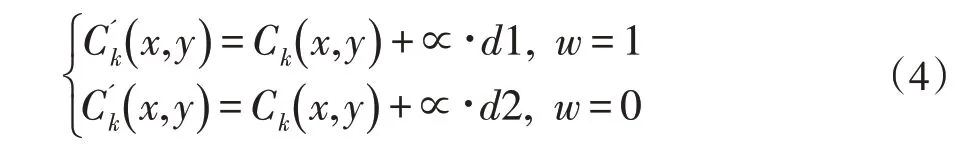
其中，Ck( x,y )表示分块的DCT 系数，( x,y )为DCT系数的坐标，其中k=1,2,…,1024，∝表示嵌入水印的强度因子，w 表示水印信息，为嵌入水印后的DCT 系数。水印信息提取时，我们根据嵌入水印位置的DCT 系数与随机矩阵的相关性进行分析，如果与d1 相关性高，则说明嵌入的水印为1，反之，嵌入的水印为0，从而实现了水印信息的盲提取。计算嵌入水印序列与随机矩阵相关性[10]的公式如下：

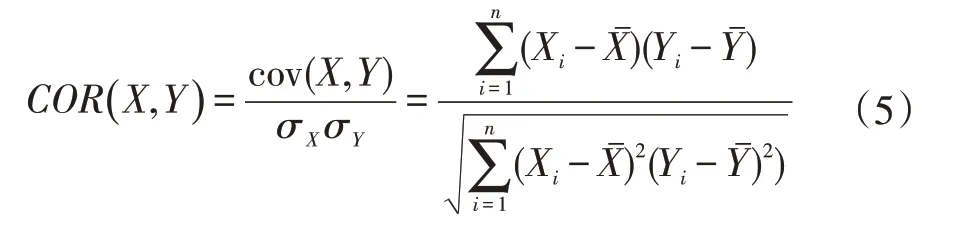
水印的嵌入流程如图4 所示。

图4 水印嵌入流程图

提取水印为嵌入水印的逆过程，根据公式（10）即可还原水印图像，本文利用峰值信噪比（PSNR）对含水印图像的性能进行测试，利用归一化值（NC）对提取的水印图像的性能进行评价。当嵌入鲁棒性水印时，由于主要选择低频部分进行嵌入，因此PSNR 的值在30～40 左右，即可保证含水印图像的透明性，NC 值主要反映提取水印质量，当趋近于1 时，说明提取的质量较好，一般来讲，当NC 值低于0.8 时，提取的水印图像则不可辨认。

3 仿真实验

本文选择MATLAB 2018 仿真平台，根据嵌入算法，进行了多种类型、多种强度的模拟实验，通过仿真实验得知当嵌入强度因子在20～35 之间，本算法均可以表现出较好的性能，本实验过程中我们使用的强度因子为30。原始载体图像与含水印图像如图5 所示。

通过对比可以得知，含水印与原始载体图像并无明显差别。通过计算，峰值信噪比为38.6487，说明嵌入的水印信息具有良好的不可见性，对载体图像几乎没有影响。

图5 原始载体图像与含水印图像对比

然后我们对载体图像进行多种类型的攻击实验，并计算攻击后含水印图像与原始载体图像的峰值信噪比（PSNR）以及提取的水印的归一化值（NC），通过计算得到的PSNR 值与NC 值对水印算法的性能进行评价，具体实验过程如下。

图6 JEPG压缩后提取的水印

表1 JEPG 压缩攻击后的性能

如图6 与表1 所示，JPEG 压缩攻击时，当品质因素从80 递减到30 时，含水印图像的PSNR 值都在30以上，因此含水印图像透明性较好，而提取水印的归一化值也趋近1，质量非常理想。

图7 椒盐噪声攻击后提取的水印

如图7 与表2 所示，当椒盐噪声的强度从0.001 增加到0.01 时，含水印图像的PSNR 从30.5272 开始减小，说明载体图像质量下降明显，而提取的水印信息仍在0.96 以上，性能良好。

表2 椒盐噪声攻击后的性能

图8 多种类型攻击后提取水印

表3 多种类型攻击后的性能

如图8 与表3 所示，我们对载体图像进行六种类型的模拟攻击。其中维纳滤波、缩放、中值滤波含水印图像的PSNR 值都在30 以上，含水印图像质量很好，而旋转、剪切、高斯噪声的攻击后，含水印图像的PSNR值下降明显，说明对原图影响较大。而整体上提取水印的NC 值都在0.9 以上，表现出较好的性能。

4 结语

本文提出了一种在DWT_DCT 变换域内利用随机矩阵嵌入水印的算法，并得到以下结论。

（1）利用DWT 的多分辨率特性、DCT 系数的统计特性并结合HVS 的特点，提出了一种DWT 与DCT 相融合的水印算法，保证了含水印图像的透明性以及提取水印的鲁棒性。

（2）利用Arnold 置乱算法与混沌加密的双重加密算法，保证了嵌入水印的安全性。

（3）利于随机矩阵嵌入水印的方式，使得系统每次都产生不同的两个八位序列，因此每次提取水印都需要不同的密钥，从而进一步提高了算法的安全性。

（4）通过各种类型、不同强度的模拟攻击，本水印算法均能够够有效地提取到水印信息，并且实现了水印信息的盲提取。