基于分类思想的改进粒子群优化算法

仝秋娟 李萌 赵岂

摘  要： 针對粒子群算法存在收敛速度慢、收敛精度低且易收敛到局部极值的问题，提出一种基于分类思想的粒子群改进算法。该算法将粒子适度值和适度值均值做差与适度值标准差进行比较，从而将粒子所在区域划分为拒绝域、亲近域、合理域。根据不同区域中粒子的特点选取不同惯性权重和学习因子，使粒子高效地选择自身经验或种群经验，合理增强或减弱粒子全局搜索能力和局部搜索能力。数值实验结果表明，与其他粒子群改进算法相比，新的分类粒子群算法有效加快了粒子的收敛速度，提高了算法的收敛精度，有效改善了算法寻优性能。

关键词： 粒子群优化; 参数改进; 适度值; 适度值均值; 适度值标准差; 粒子分类; 有效经验

中图分类号： TN911.1?34; TP18                     文献标识码： A                   文章编号： 1004?373X（2019）19?0011?04

Abstract： In order to solve the problems of slow convergence speed， low convergence precision and easy convergence to local extremum， an improved particle swarm optimization algorithm based on classification is proposed. The difference between the moderate value and the mean of moderate value is compared with the standard deviation of moderate value in this algorithm， then the region where the particles are located is divided into rejection domain， close proximity domain， and reasonable domain. According to the characteristics of particles in different regions， different inertia weights and learning factors are selected to ensure that the particles can efficiently select their own experience or population experience， and reasonably enhance or weaken the global search ability and the local search ability of the particles. The numerical results show that， in comparison with other particle swarm optimization algorithms， the proposed particle swarm optimization algorithm can more effectively accelerate the convergence speed of particles， and improve the convergence precision and optimization performance of the algorithm.

Keywords： particle swarm optimization; parameter improvement; moderate value; mean of the moderate value; standard deviation of moderate value; particle classification; effective experience

0  引  言

粒子群优化算法（Particle Swarm Optimization，PSO）是受到鸟鱼群搜索食物策略的启发而提出的一种群智能优化算法[1]。它以随机解为出发点，用适度值评价解的优劣，通过迭代寻找最优解。相比其他智能算法，PSO算法设置参数少、迭代快、易理解、工程上易实现。目前PSO算法在函数优化[2]、神经网络训练[3]、图像处理[4]以及其他工程领域都得到了广泛应用。但该算法没有严格的理论指导，收敛精度低、易收敛到局部极值。对此，学者们提出各种改进算法，有基于模式结构的改进、基于种群多样性的改进、基于参数改进等[5?7]。其中，对算法参数的改进是一个重要方向。文献[8]先将惯性权重系数引入粒子速度更新公式中，后又加以改进，使惯性权重系数线性递减[9]，有效加快了算法收敛速度。文献[10]提出基于时间变化的学习因子的改进，动态调节前后期粒子的搜索策略，加快了算法的收敛速度，但在多峰函数中极易陷入局部最优。文献[11]提出一种用正弦函数调节惯性权重的改进算法，提高了算法的收敛速度。但是这些方法在收敛精度上依然有所欠缺。

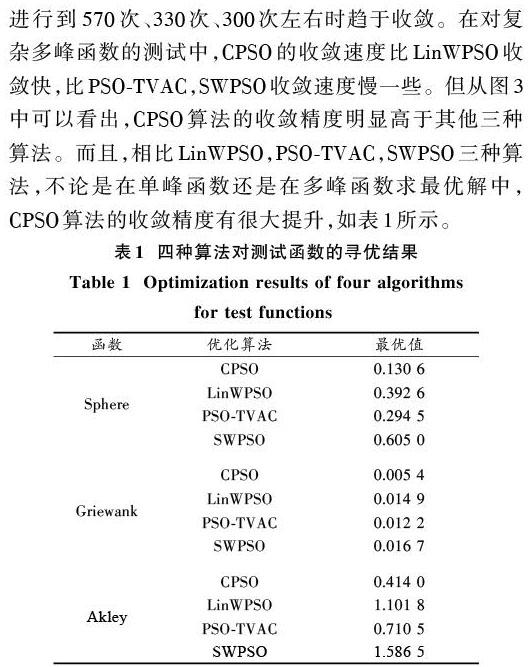
綜上所述，无论是在求解单峰函数还是复杂的多峰函数，基于分类思想的改进算法在收敛速度和收敛精度上整体优于另外三种算法。

4  结  语

本文提出一种基于分类思想的粒子群优化算法，改变了传统算法中粒子采取统一迭代公式的做法，针对不同区域的粒子，利用不同的惯性权重系数和学习因子对粒子的全局寻优能力和局部寻优能力进行合理地调整。实验结果表明，相比一些传统的算法，新算法不仅收敛速度有所提升，收敛精度也有所提高，算法寻优性能明显改善。将此算法应用到其他领域是下一步的研究方向。

参考文献

[1] KENNEDY J， EBERHART R C. Particle swarm optimization [C]// Proceedings of IEEE International Conference on Neural Networks. Perth： IEEE， 1995： 1942?1948.

[2] 周勇，胡中功.改进的快速遗传算法在函数优化中的应用[J].现代电子技术，2018，41（17）：153?157.

ZHOU Yong， HU Zhonggong. Application of improved fast?convergent genetic algorithm in function optimization [J]. Modern electronics technique， 2018， 41（17）： 153?157.

[3] 李钰曼.改进的PSO?RBF神经网络在复杂工业过程中的应用[D].石家庄：河北科技大学，2018.

LI Yuman. Application of improved PSO?RBF neural network in complex industrial processes [D]. Shijiazhuang： Hebei University of Science and Technology， 2018.

[4] 吕微微，张宏立.基于协同进化粒子群算法的系统辨识[J].计算机仿真，2016，33（1）：336?339.

L? Weiwei， ZHANG Hongli. Identification of system co?evolution based on particle swarm optimization algorithm [J]. Computer simulation， 2016， 33（1）： 336?339.

[5] 章云霞.基于粒子群算法的结构损伤诊断研究[D].柳州：广西科技大学，2015.

ZHANG Yunxia. Research on structural damage detection based on particle swarm optimization algorithm [D]. Liuzhou： Guangxi University of Science and Technology， 2015.

[6] 王博建.粒子群算法在复杂函数优化中的学习策略及其改进[D].南昌：华东交通大学，2018.

WANG Bojian. The learning strategy and improvement of particle swarm optimization in complex function optimization [D]. Nanchang： East China Jiaotong University， 2018.

[7] 段晓东，王存睿，刘向东.粒子群算法及其应用[M].沈阳：辽宁大学出版社，2007：42?74.

DUAN Xiaodong， WANG Cunrui， LIU Xiangdong. Particle swarm optimization and application [M]. Shenyang： Liaoning University Publishing House， 2007： 42?74.

[8] SHI Y H， EBERHART R C. A modified particle swarm optimizer [C]// 1998 IEEE International Conference on Evolutio?nary Computation Proceedings. Anchorage： IEEE， 1998： 69?71.

[9] SHI Y H， EBERHART R C. Empirical study of particle swarm optimization [C]// Proceedings of the 1999 Congress on Evolutionary Computation?CEC99 （Cat. No. 99TH8406）. Washington： IEEE， 1999： 1380.

[10] RATNAWEERA A， HALGAMUGE S K， WATSON H C. Self?organizing hierarchical particle swarm optimizer with time?varying acceleration coefficients [J]. IEEE transactions on evolutionary computation， 2004， 8（3）： 240?255.

[11] 南杰琼，王晓东.改进惯性权值的粒子群优化算法[J].西安工程大学学报，2017，31（6）：835?840.

NAN Jieqiong， WANG Xiaodong. Particle swarm optimization algorithm with improved inertia weight [J]. Journal of Xian Polytechnic University， 2017， 31（6）： 835?840.

[12] KENNEDY J. The behavior of particles [C]// Proceedings of the Seventh Annual Conference on Evolutionary Programming. New York： [s.n.]， 1998： 581?589.