基于模糊综合评价法的高大模板支撑体系安全性评估
2019-10-14夏进,余峰
夏 进,余 峰
(武汉建工集团股份有限公司,湖北 武汉 430023)
0 引 言
随着社会的发展,越来越多的大跨度、超高度结构成为现代建筑结构主流特点,因而高大模板支撑体系也被广泛应用,但高大模版支撑体系一旦发生安全生产事故,极容易造成特别重大安全事故,给企业和国家造成重大的人员伤亡和经济损失[1]。高大模板支撑体系影响因素具有复杂性、模糊性和不确定性,给现场安全质量检查造成很大困扰[2]。本文以武汉航空企业总部区项目高支模工程作为研究对象,采用模糊综合评价法对高支模架体安全性做出估算,为现场施工人员及管理人员提供参考。
1 模糊综合评价基本理论
模糊综合评价法是依据模糊数学中的模糊集合理论,选择评价对象的因素集及评语集,并确定各因素对评价对象影响程度的权重值,再利用模糊关系合成原理,求得受多种复杂因素影响的评价对象评语等级的一种综合评价方法[3]。基本步骤如下:
1)设评价集X={x1,x2,x3,…,xn},影响因素集Y={y1,y2,y3,…,ym},U是由X到Y的模糊关系,则隶属度函数fU(xi,yi)=uij(i=1,2,…,n;j=1,2,…,m),描述了f与y之间关于U的相关程度。可得模糊矩阵,如式(1)所示。

2)对论域X上的模糊集A,a0∈A,采用 Delphi 法确定隶属度函数fA(a0),设有n位学术水平不同的专家,分别独立给出fA(a0)的估计值mi(i=1,2,…,n),计算mi的算术平均值和离差d,如式(2)所示。

式中:αi为权重,应满足αi>0 且为离差,应满足精度要求。
3)采用层次分析法(AHP)确定权重向量W,W=根据判断矩阵,求出U的最大特征值所对应的特征向量,即权重向量W。
4)对判断矩阵一致性检验。由矩阵U求出的W是否合理,需根据式(3)进行随机一致性检验。

式中:CR为一致性比率,当CR<0.1 时,认为判断矩阵通过一致性,否则重新分配判断矩阵元素取值,直至达到一致性;RI为同阶判断矩阵的随机一致性指标(见表1);CI为一致性指标;由式(4)计算:

式中:n为R的阶数;λmax为判断矩阵最大特征值,见式(5):

表1 1~10 阶判断矩阵的随机一致性指标

5)进行模糊综合评价,综合评价模型如式(6)、式(7)所示。

由于本工程考虑的因素比较综合复杂,并且每个因素对整体的影响程度不能确定,所以采用M(·,)算子,如式(8)所示。

2 高大模板支撑体系综合评价模型
以武汉航空企业总部区项目高大模板支撑体系为例,建立高大模板支撑体系安全性模糊综合评价模型。该项目由武汉建工集团股份有限公司承建,总建筑面积 37 542.61 m2,由行政办公楼、体能训练中心及食堂、倒班用房等组成。体能训练中心及食堂支模高度 14.1 m,梁截面尺寸为 400 mm×1 800 mm,根据住房城乡建设部办公厅关于实施《危险性较大的分部分项工程安全管理规定》有关问题的通知(建办质[2018]31 号),以上均为超过一定规模的危险性较大的高大模板支撑体系,如果发生安全事故,将造成重大的人员伤亡和经济损失[4-6]。
2.1 建立安全性评价集
根据高大模板支撑体系安全性的特点,一般将其评价划分为 4 个等级:优秀、良好、合格、不合格,对应点评价集,如式(9)所示。

设定vi={优秀[100,80)、良好[80,60),合格[60,40),不合格[40,0)},其中i为第i个等级,以分数区间的上限值组成评价集,如式(10)所示。
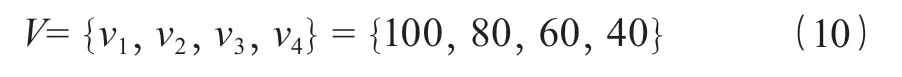
2.2 建立评价因素集
本工程邀请了高大模板支撑体系方面的10位专家组成的专家组,根据专家组意见及现场实际施工情况,确定了对该工程安全性影响较大三个主要因素施工安全管理、专项施工方案及现场施工情况,并按式(2)对各因素进行了打分。建立评价因素集,如表2所示。

表2 评价因素集
2.3 层次分析法确定各因素权重
1)第1 级因素集权向量。
第1 级因素集为:
W={W1,W2,W3}={施工安全管理,专项施工方案,现场施工情况}
根据专家意见得出判断矩阵B,并进行权重值计算和一致性检验,如表3所示。

表3 判断矩阵 B 及权重值
表中CR<0.1,判断矩阵B一致性良好,权数分配合理。
2)第2 级因素集权向量。
W1={W11,W12,W13,W14}={施工安全管理规章制度,管理人员素质,现场安全保障措施,安全教育培训及技术交底}
根据专家意见得出判断矩阵B1,并进行权重值计算和一致性检验,如表4所示。
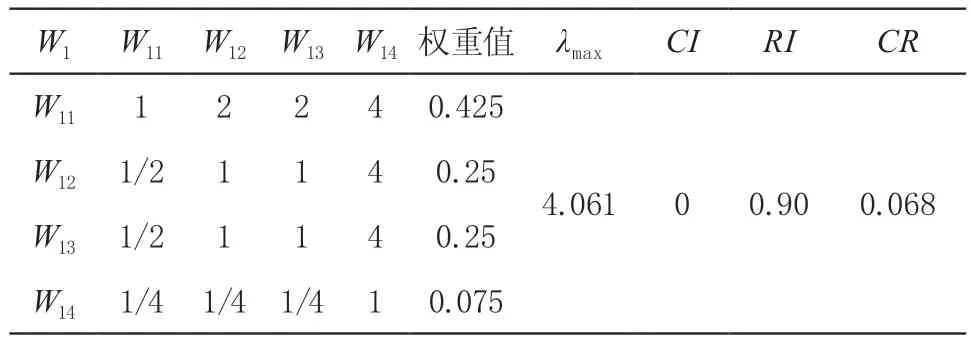
表4 判断矩阵 B1 及权重值
表中CR<0.1,判断矩阵B1一致性良好,权数分配合理。
W2={W21,W22,W23}={高大模板支撑体系设计,专家论证,理论计算}
根据专家意见得出判断矩阵B2,并进行权重值计算和一致性检验,如表5所示。

表5 判断矩阵 B2 及权重值
表中CR<0.1,判断矩阵B2一致性良好,权数分配合理。
W3={W31,W32,W33,W34}={高大模板支撑体系材料,现场搭设质量,混凝土浇筑顺序,高大模板支撑体系拆除}
根据专家意见得出判断矩阵B3,并进行权重值计算和一致性检验,如表6所示。

表6 判断矩阵 B3 及权重值
表中CR<0.1,判断矩阵B3一致性良好,权数分配合理。
根据以上内容得到评价因素权重,如表7所示。
2.4 建立隶属度函数并计算各因素隶属度
采用半梯形分布与梯形分布可以实现得分较高表示状态较好,因此本文采用半梯形分布与梯形分布建立的各级别评语对应的隶属度函数,见式(11)~(14)。
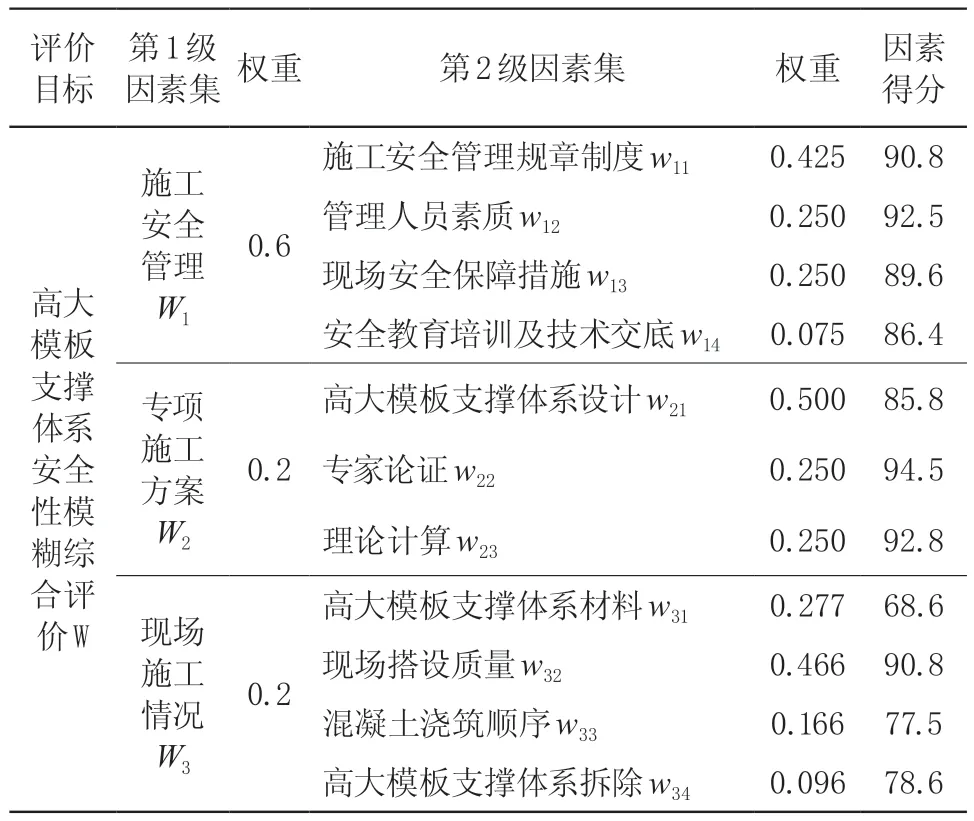
表7 评价因素权重值及得分
1)优秀。

2)良好。

3)合格。

4)不合格。

以施工安全管理规章制度为例,其得分为:90.8 分,根据式(11)~(14)计算各隶属度。
“优秀”的隶属度为:u11=0.72;
“良好”的隶属度为:u12=0.28;
“合格”的隶属度为:u13=0;
“不合格”的隶属度为:u14=0。
以此类推,可得第2 级因素的隶属度,如表8所示。

表8 第2 级因素隶属度
2.5 模糊综合评价
2.5.1 一级模糊综合评价
1)W1因素集模糊综合评价:

2)W2因素集模糊综合评价:
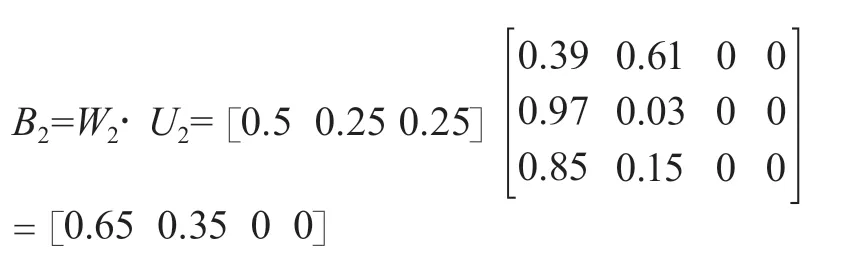
3)W3因素集模糊综合评价:

从而得出一级模糊评价结果,如表9所示。

表9 一级模糊评价结果
2.5.2 二级模糊综合评价
由二级模糊矩阵U及权向量W可计算得出二级模糊评价结果B。

对该结果进行归一化处理得:
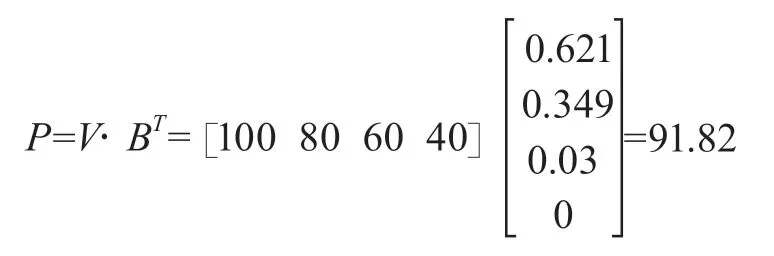
由以上结果可知,该工程高大模板支撑体系安全性评价结果优秀,与该工程实际施工相符,施工过程中没有发生安全事故,施工圆满完成。
3 结 语
采用模糊综合评价法对影响高大模板体系安全性的因素进行评估,对现场施工人员检查高大模板支撑体系具有一定借鉴意义,在有完善的施工安全管理规章制度前提下,应严格按照专项施工方案实施,并实时监测现场施工情况,这样才能确保高支模施工安全和混凝土观感质量满足要求。
