基于模糊逻辑算法的感应式信号灯仿真设计

李晓玲 刘 秀 王 琪

(东北林业大学交通学院,黑龙江 哈尔滨 150040)

随着我国国民经济水平及出行要求的不断提高，我国汽车保有量不断提升，在方便了人们出行的同时也给城市道路造成了极大的压力[1]。在高峰时段城市主干道路与支路交叉口之间的冲突是造成拥堵的主要问题之一[2]，由于支路的集散功能有着很强的时间差异，非高峰时段汇入主路的车辆数大大减少[3]，主路与支路的车流比变化明显，因此主干路与支路交叉口使用固定信号控制势必会降低非高峰时段主路车流的运行效率[4]。

我国在20世纪初才开始了交通信号控制系统方面的研究，并直到20世纪70年代，我国才逐渐引进和投入使用了感应式、定周期相关的信号控制方式[5]。随后在1980年开始实施了通过计算机来进行干道协调控制和感应控制[6]。但现在国内仍大量存在因交通信号配时不当而引起拥堵的现象，这对道路安全及交通管理均带去了大量不便之处。国外的交通控制系统也是在这样不断发现问题后不断修复中得到提高。如今较为广泛运用的信号控制系统有以下三种[7]：一是TRANSYT系统[8]；二是SCOOT系统[9]；三是SCATS系统[10]。

研究的是一种基于模糊逻辑算法的感应式信号灯，旨在通过给予模糊逻辑算法的自适应控制来提高主干路与支路交叉口通行效率。主要根据主干路与支路的车流量比及资源利用程度得出合理的配时，对应算法得出针对主支路交叉口信号配时的优化方案，以缓解交通拥挤问题。

1 研究整体思路

将根据主干路与支路的车流量比作为输入量，结合模糊逻辑，得出对应控制量及配时方案，后经反馈得以连续，用以缓解主干路与支路信号交叉口的交通拥挤问题，大体结构如图1所示。

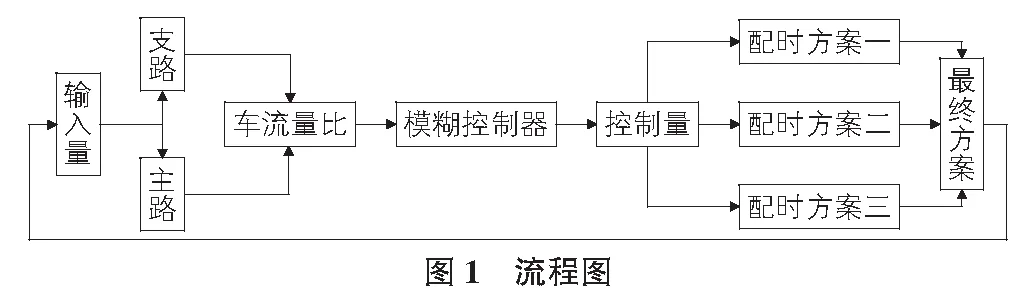
2 模糊控制器设计

美国自动控制专家Zedeh于1965年发表了他的著名论文“模糊集合”(Fuzzy Sets)，开辟了模糊控制的新领域[11]。通过matlab等相关软件可以轻易的看出，当隶属度函数的值越接近1，变量隶属于模糊集合的程度越高，反之隶属度函数的值越接近0，则表示变量隶属于模糊集合的程度越低[12,13]。

2.1 隶属度函数

采用人工计数在司徒街—六顺街信号交叉口所得的数据及相关理论绘制了如下函数：选择主路与支路流量比e为观察量，选取配时方案u为控制量，将e划分为3个模糊集，选取语言变量值为负大(NB)、零(ZO)、正大(PB)。根据实际情况，设定e的取值范围为[1,9],输入量e隶属度函数如图2所示。且以上每一板块均为数据压缩下对应的语言变量，而输入数值的定性便由隶属函数来判断[14]。

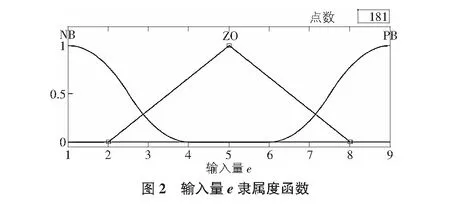
由此得到比值e对应的模糊控制表如表1所示。

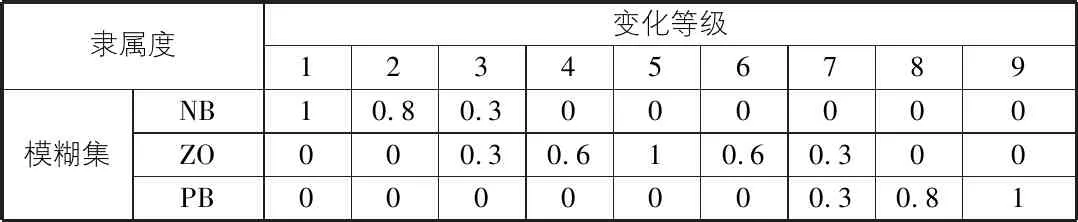
表1 e变量的模糊集

同样，将控制量u设置为3个级别，分别为负大(NB)、零(ZO)、正大(PB)设定u的取值范围为[-1,1]，控制量u隶属度函数如图3所示。

由此得到控制量u对应的模糊控制表如表2所示。

根据所确定控制量的模糊集，制定配时方案Ⅰ，配时方案Ⅱ和配时方案Ⅲ。

表2 u变量的模糊集

2.2 模糊规则

制定模糊规则：采用“IF A THEN B”的规则，描述为：当e为负大(NB)时，应采取配时方案Ⅰ，其对应的控制量u的语言变量值为负大(NB)；当e为零(ZO)时，应采取配时方案Ⅱ，其对应的控制量u的语言变量值为零(ZO)；当e为正大(PB)时，应采取配时方案Ⅲ，其对应的控制量u的语言变量值为正大(PB)。根据上述制定的模糊规则，得到模糊关系集合R。

至此，模糊控制量u便可由输入量e与模糊集合R合成求出，具体表达式如式(1)所示。

u=e⊙R

(1)

2.3 控制器实现

通过MATLAB仿真得到的模糊面图和模糊函数图见图4，图5。

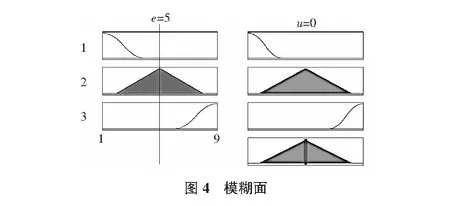
3 VISSIM模拟仿真

经过实地调查，哈尔滨市香坊区司徒街—六顺街交叉口符合本方案适用条件。其中，东西向为主干道，南北向为支路，车流量相差较大，仿真数据取自该交叉口高峰时段。

仿真采用人工计数法对司徒街—六顺街信号交叉口高峰时段进行调查，得到高峰时段车流量。经过实地调查，该信号交叉口为三相位交叉口，相位设置如图6所示。

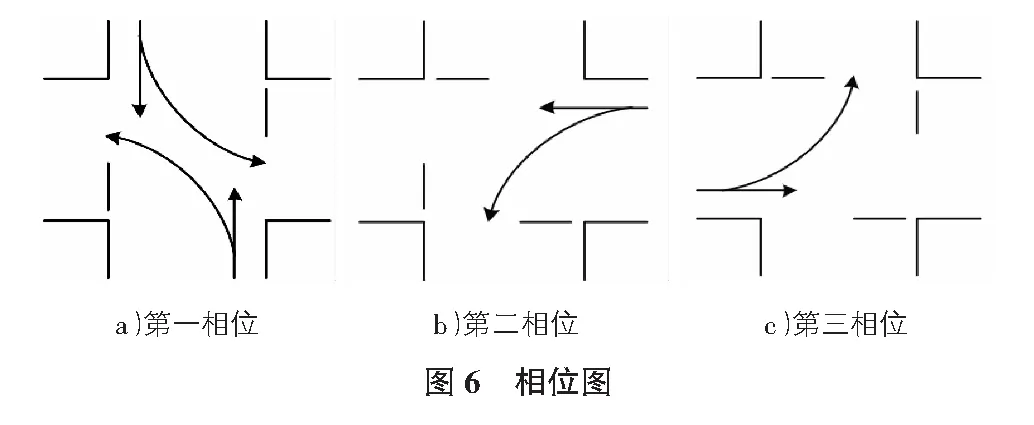
采用韦伯斯特配时法进行信号配时，具体算法如式(2)～式(6)所示。

(2)

Ge=T-L

(3)

(4)

g=ge-A+1

(5)

(6)

其中，T为最佳周期长度;Y为周期长度内各相位最大饱和度yi值之和;L=∑(l+I-A)为每个周期的损失时间;I为绿灯间隔时间;l为起动损失时间;A为黄灯时间;Q为某进口的交通量;C为对应Q的设施通行能力。计算得到配时方案如表3所示。

表3 配时方案 s

4 仿真结论

通过VISSIM仿真，将根据实际情况随机产生的车流量比，使用该配时方案与原有配时方案进行对比。

当支路与主路的流量比为1∶10时，仿真结果如表4所示。西进口延误下降37.4%，东进口延误下降72.3%。当支路与主路的流量比为1∶5时，仿真结果如表5所示。西进口延误下降8.23%，东进口延误下降6.73%。

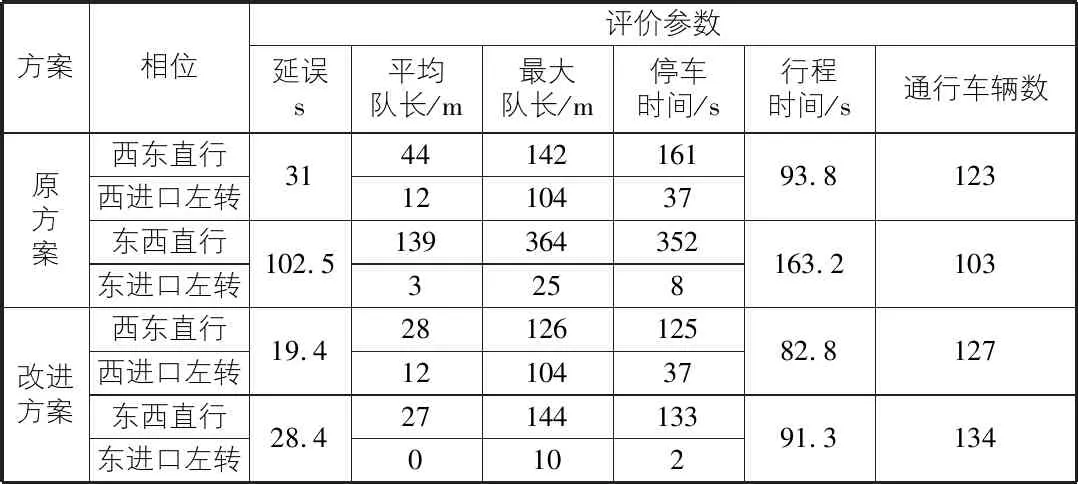
表4 仿真结果(流量比为1∶10)

表5 仿真结果(流量比为1∶5)

5 算法改进

在一元输入的基础上，考虑其他因素进行多因素融合分析来进一步提高方案的效率。选取进入该交叉口的机动车与非机动车的交通构成比例作为增加输入量m，其论域为{0，1}；通过仿真

实验各项指标均优于先前所提方案。