关于傅里叶变换与振幅关系的思考

赵焕青

（中北大学信息商务学院，晋中 030600）

关于傅里叶变换，很多文章只是告诉这么操作一下就可以得到正确结果，没有解释为什么这样做，往往会让人觉得“不明觉厉”，仿佛是一种魔法。但是一旦理解了它是一种分解操作，理解了“基函数”的意义，理解了傅里叶变换与幅度的关系，我们就很容易理解为什么要做、怎么做、为什么这样做。下面我们一一来论述。

1 简谐振动的三要素

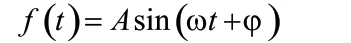
2 简谐振动的叠加性

一个比较复杂的周期运动可以看成是许多不同频率的简谐振动的叠加。

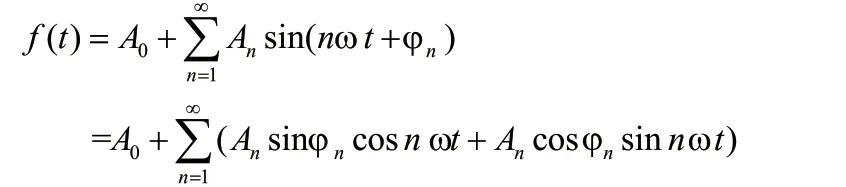
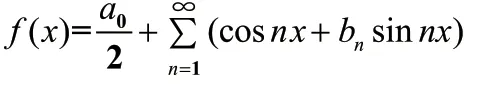
3 简谐振动叠加的唯一性

根据线性空间中的正交性质，级数展开是唯一的。

3.1 函数的内积是向量内积概念的推广

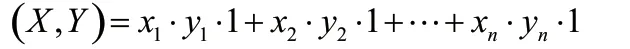
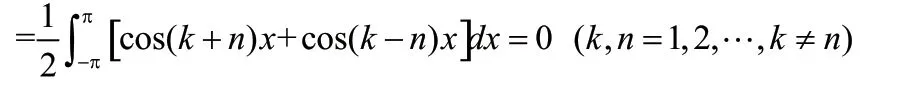
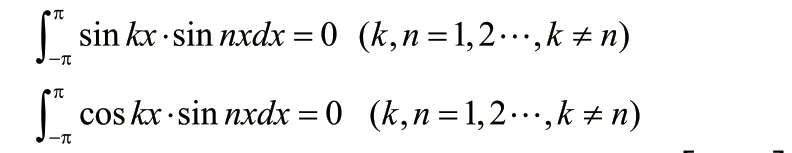
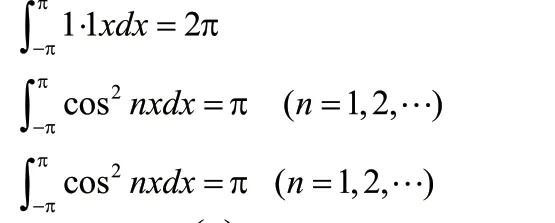
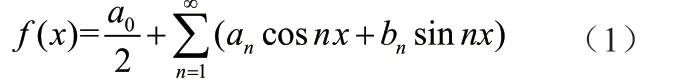
右端级数可逐项积分

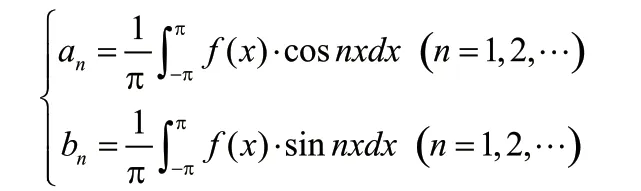
3.2 周期函数的傅里叶级数展开是唯一的

基波角频率为1的非正弦周期函数的傅里叶级数（1）说明以

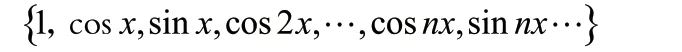
为基的无限维线性空间中的向量总是可以由这些正交基向量叠加出来，叠加系数就是与各基向量求内积得到。周期函数的傅里叶级数就是它在内积空间上的正交分解，分解是唯一的。

4 频谱函数与振幅的关系

4.1 傅里叶级数

4.2 傅里叶变换

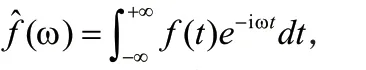
傅里叶逆变换是用复指数信号的和表示各种形式的信号，复指数信号频率不同，他们的频率是原信号频率的整数倍。这些信号是高频信号，他们修饰与原信号频率相同的信号，使得傅里叶逆变换就等于原信号。频谱上的最低频率就是原信号频率，对应的幅值最大的。

傅里叶逆变换是在频率上求和，不是在时域上。那么，我们可以隔一段时间采集一次信号，然后作傅里叶变换，观察信号在频域上随时间的变化。

5 结束语

傅里叶变换在许多领域有着广泛的应用，比方说物理学、电子类学科、信号处理、海洋学。本文有助于我们深刻理解并掌握傅里叶变换的内涵。