基于密度的Top-n局部异常点快速检测算法
2019-10-14齐建鹏于彦伟赵金东
刘 芳 齐建鹏 于彦伟 曹 磊 赵金东
近年来,随着各类智能移动设备的广泛普及,社交网络、网上购物、移动支付、位置服务等新兴应用不断涌现,各类海量大数据被采集和处理,而面向这些大数据的挖掘分析服务已俨然成为一大独具特色的新兴产业.异常检测作为数据挖掘最重要的任务之一,在网络监测、信用卡欺诈、电信诈骗、金融证券服务、电子商务等各种应用领域都被认为是至关重要的内容.因此,异常检测在学术界与工业界都受到了越来越多的关注,在大数据与人工智能应用中,异常检测也发挥了越来越重要的作用,例如在北京,通过对地铁和公交乘车记录的异常检测分析可帮助安保系统识别出潜在的小偷[1].
异常检测旨在从海量数据中识别出与大多数数据样本差异较大的数据对象.目前已存在很多异常检测研究工作[2−4],如基于距离的异常检测[5−7]、基于邻居的异常检测[8−10]、基于分布的异常检测[11−13]和基于聚类的异常检测[14−15]等.然而,这些异常检测方法都无法处理数据倾斜分布下的异常检测问题,因为在倾斜分布的数据中,不同区域的异常数据可能具有不同的数据特征,而上述方法都采用全局的异常标准来处理数据对象.基于密度的LOF[16]有效解决了在数据倾斜分布下的异常检测问题.局部异常检测利用每个数据对象相对于其周围邻居的相对密度衡量异常因子,这样的相对密度反映了局部的数据分布,也就是说,对异常的检测是相对于局部数据的,因此可以处理倾斜分布下的异常检测问题.在实际应用中,尤其是在大数据系统中,数据的分布往往是倾斜的,基于LOF 的局部异常检测方法相比其他检测方法在很多应用领域都表现出了较好的异常检测效果[17−18].
局部异常检测方法[16]需要计算每个数据对象的LOF 异常因子,然后通过排序找出LOF 值较大的数据点作为异常对象,而LOF 定义了相对密度,要求查找每个数据的k近邻及可达距离,因此检测计算成本非常高,很难满足对大规模数据的异常检测效率需求.最新研究[19]针对Top-n局部异常点检测,提出了一种基于LOF 上界剪枝的检测算法(Top-nLOF,TOLF),利用Cell 索引和LOF 上界对数据对象进行剪枝,较大地提升了局部异常点检测的效率.尽管如此,TOLF 在Cell 剪枝中仅采用了一个全局的两点间最小距离cpmin进行剪枝,当全局cpmin较小时,将严重影响Cell 剪枝效果,甚至失效,此外,针对数据对象剪枝的LOF 上界相比真实LOF 值较大且计算复杂度较高,使得剪枝效果也有限.
针对这些问题,本文提出了一种改进的Top-n局部异常点检测算法MTLOF,融合索引结构和多层LOF 上界设计剪枝策略,实现了高效的局部异常点检测.1)为避免直接计算LOF 值,提出了四个更接近真实LOF 值的LOF 上界(UB1−UB4),并对它们的计算复杂度进行了理论分析;2)利用索引结构和UB1、UB2上界,提出了两层的Cell 剪枝策略,不仅采用全局Cell 剪枝策略,还引入了基于Cell 内部数据对象分布的局部剪枝策略,有效解决了高密度区域的剪枝问题;3)利用提出的UB3和UB4上界,提出了两个更加合理有效的数据对象剪枝策略,UB3和UB4上界更加接近于真实LOF 值,有利于剪枝更多数据对象,而基于计算复用的LOF上界计算方法,大大降低了计算成本;4)优化了初始候选Top-n局部异常点的选择方法,利用均匀区域划分和建立的索引结构,在数据分布的稀疏区域选择初始局部异常点,有利于选择LOF 值较大的数据对象作为初始局部异常点,有效提升初始临界值(Cutoff threshold)ct,使得在初始阶段剪枝掉更多的Cell 和数据对象.5)在六个不同维度的真实数据集上的综合实验评估验证了MTLOF 算法的高效性和可扩展性,相比最新的TOLF 算法,提升的效率可高达3.5 倍.
本文结构如下:第1 节讨论相关工作;第2 节定义基本概念和问题;第3 节给出详细的检测算法;第4 节进行实验验证和分析;第5 节总结全文.
1 相关工作
Breunig 等[16]最早提出了局部异常因子LOF的概念,相对基于距离的异常检测[5−6]和KNN 异常检测[9],LOF 采用相对密度衡量每个数据对象的异常程度,LOF 越高表示数据对象相对于其邻居的密度差异较大,异常的可能性也就越高.异常通常只是数据集的极少部分,因此Jin 等[20]首次提出了Top-n局部异常的概念,从数据集中选取n个LOF 值最大的数据对象,即为Top-n局部异常.传统LOF 挖掘方法[16]主要分为两步:首先计算出所有数据对象的LOF 值,然后对所有数据按LOF 值降序排序,前n个数据对象即为Top-n局部异常.文献[20]首先利用Birch 算法[21]对数据对象进行聚类,利用聚簇的半径和聚簇间的距离关系计算每个聚簇的LOF 界值,对聚簇进行排序,然后在最可能包含异常的聚簇中检测Top-n局部异常点.虽然该方法通过聚类方法剪枝掉了部分数据对象,但是数据预处理计算成本昂贵,不适用于大数据的处理.此外,算法的剪枝策略也具有较大局限性,并没有表现很好的剪枝效果.
另外一类相关工作就是LOF 的变种方法,Tang 等[22]提出了一种基于连通性的异常检测方法(Connectivity-based outlier factor,COF),COF首先利用最小生成树衡量每个数据对象与它k近邻的连通度,然后与LOF 相似,利用相对k近邻连通度定义每个数据对象的COF.为了优化基于最小生成树聚类的异常检测,朱利等[23]提出了一种快速构建最小生成树的优化方法,可同时检测基于距离的全局异常和基于密度的局部异常,但是这类基于扫描树的聚类方法无法处理大规模数据,如文献[23]中性能验证,在处理1 800 个数据点时已消耗近60秒.Papadimitriou 等[24]提出了一种局部相关度方法(Local correlation integral,LOCI),LOCI 采用一个区域半径r定义数据对象的本地邻居区域,以代替k近邻.虽然LOCI 相比LOF 具有较低计算复杂度,但是在数据倾斜分布下,通过固定区域半径定义局部异常并不合理,可能导致稀疏区域的数据对象没有邻居点而高密度区域的数据对象包含过多的邻居点.杨宜东等[25]为了减少计算时间,还提出了一种动态网格划分的数据流下的LOCI 异常检测方法.Zhang 等[26]提出了一种基于距离的局部异常点检测(Local distance-based outlier factor,LDOF),LDOF 采用数据对象到其k近邻距离的均值定义数据对象的局部密度,然后相对k近邻计算相对密度获得异常因子.与文献[26]相似,Krieget 等[27]则使用数据对象到其k近邻距离的平方和的均值来定义局部密度.最近,Schubert 等[28−29]又提出了一种更为简单的LOF 变种方法,称为Simplified-LOF,该方法直接使用k-距离代替可达距离,也就是说,直接使用k-距离的倒数定义局部密度.该方法虽然简化了LOF 方法,但是仅考虑每个数据对象到第k个近邻的距离,将导致异常检测效果严重依赖于参数k的选取.此外,Liu 等[30]将局部异常检测扩展到了不确定数据领域上,研究了在概率密度表示的不确定数据模型上的异常检测方法.最近Cao 等[31−32]还考虑了在属性级不确定数据上的Top-n局部异常点检测方法.
Liu 等[33−34]提出一种基于隔离树的快速异常检测算法(Isolation forest,Iforest),该方法首先随机采样m个数据对象样本,构建多棵Itree 隔离树(Isolation trees),然后对每个数据对象来遍历这些Itree,根据数据对象经过的平均路径长度来判断是否为异常对象.Iforest 虽具有线性的时间复杂度,但并不适用于特别高维数据,因为每次切割数据空间都是随机选取一个维度,建立隔离树后仍有大量维度信息没有使用,导致算法可靠性降低.此外,Iforest 算法也仅对全局异常敏感,不擅长处理局部的相对稀疏点,即本文处理的局部异常点.为了加快Top-n局部异常点检测,最新研究[19]提出了一种基于Cell 索引和LOF 上界剪枝的TOLF 算法,TOLF 首先将数据集划分成多个相对均匀的区域,并对相对密集的区域建立Cell 索引,然后利用Cell索引和LOF 上界对Cell 和数据对象进行剪枝.尽管TOLF 有效提升了Top-n局部异常点的检测效率,但是采用全局最小距离的Cell 剪枝策略具有一定局限性,当存在较多过密区域时(最小距离非常小),将严重影响Cell 剪枝效果,甚至失效.此外,TOLF 所采用的面向单个数据对象剪枝的LOF 上界相比数据对象真实LOF 值较大,导致数据对象的剪枝空间有限.
2 问题定义
本节首先介绍LOF[16]相关定义,然后给出Top-n局部异常点检测的问题定义.
基于密度的局部异常根据每个数据对象本地的密度与它k近邻的密度的比值判断该数据对象是否是一个局部异常点.对于两个数据对象p和q,本文使用dist(p,q)表示它们间的距离.所有数据对象集合表示为D.
定义1(k 近邻).给定数据对象p和任意正整数k,数据对象p的k近邻集合由到p距离最近的k个数据对象组成,表示为Nk(p).
定义2(k-距离).给定数据对象p和任意正整数k,距离p第k个最近的数据对象记为qk,p的k-距离则是p到qk的距离,记为distk(p).
也就是说,对于任意q ∈Nk(p),dist(p,q)≤distk(p).
定义3(可达距离).给定数据对象p和q ∈Nk(p),数据对象p相对于q的可达距离distr(p,q)定义如下:distr(p,q)=max{dist(p,q),distk(q)}.
根据定义3,如果对象p也是q的k近邻,也就是说p ∈Nk(q),则p相对于q的可达距离就是distk(q);反之,则为两对象的距离dist(p,q).
定义4(k 近邻可达距离和).给定数据对象p,数据对象p的k近邻可达距离和distkr(p)定义如下:
定义5(局部可达密度).数据对象p的局部可达密度(Local reachability density,LRD)表示为:
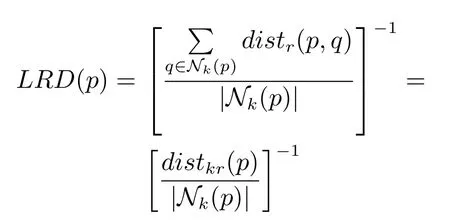
从定义5 可知,LRD(p)就是数据对象p相对于其k近邻的可达距离的均值的倒数,也就是说,局部可达密度主要通过数据对象相对于其k近邻的可达距离来估计它的局部密度.数据对象相对于其k近邻的可达距离均值越小,也就是说相对越密集,它的局部可达密度就越高.接下来根据LRD(p)来定义数据对象的局部异常因子LOF.
定义6(局部异常因子).数据对象p的局部异常因子表示为:
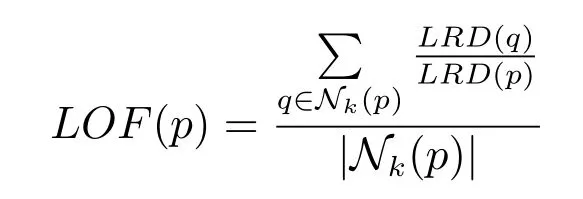
很明显,LOF(p)就是数据对象p的所有k近邻的局部可达密度与p的局部可达密度比值的均值.因此,LOF(p)越接近于1,说明对象p与其k近邻的局部密度越接近,p的异常程度越小;LOF(p)小于1 时,则说明对象p处于一个高密度区域.相反,LOF(p)值越大,则表示p是异常点的可能性越大.所以本文的关注点在于快速检测出具有较高LOF的数据对象,下面给出本文所要解决的Top-n局部异常点检测的问题定义.
问题1(Top-n 局部异常点检测).给定数据集合D,对象近邻数k,和异常点数量n,Top-n局部异常点检测则是返回数据集D中LOF 值最大的前n个数据对象.
3 基于密度的Top-n局部异常点检测
本节将详细介绍本文所提出的Top-n局部异常点检测的优化算法,首先介绍基于临界值剪枝的检测算法,然后介绍优化算法用到的四个LOF 上界,接着介绍基于LOF 上界的剪枝策略,最后给出优化的检测算法.
3.1 基于临界值剪枝的检测算法
为了获取LOF 值最大的前n个数据对象,即Top-n局部异常点,传统的基本方法将计算出所有数据对象的LOF 值,然后按照LOF 值排序,返回前n个数据对象.然而,对于Top-n局部异常点,并不需要计算出所有数据对象的LOF 值,我们仅关心LOF 值最大的n个数据对象,因此,只需要维护LOF 值最大的n个数据对象即可.
给定数据集D,从中随机选取n个数据对象,并计算它们的LOF 值,选取最小的LOF 值作为临界值(Cutoff threshold,ct).可以发现,对于数据集D中任意的数据对象p,如果LOF(p)
从定义6 可知,直接计算数据对象LOF 值的成本较高,为了更高效地检测出Top-n局部异常点,我们将从四个方面优化基于临界值剪枝的检测方法:1)如何快速获取到LOF 值较大的n个数据对象作为初始维护的候选异常对象;2)选取更合理有效的LOF 值上界进行剪枝判断,以避免直接计算数据对象的LOF 值;3)如何使用数据对象的这些LOF 值上界,使得计算量尽量小,且被剪枝掉的数据对象数量尽量多;4)如何结合索引技术和LOF 上界快速剪枝掉高密度区域的所有数据对象.
3.2 LOF 上界
本小节将首先介绍数据对象LOF 值的四个上界,然后分析四个上界的计算时间复杂度.
3.2.1 四个LOF 上界
根据定义5 和定义6 可以得出:
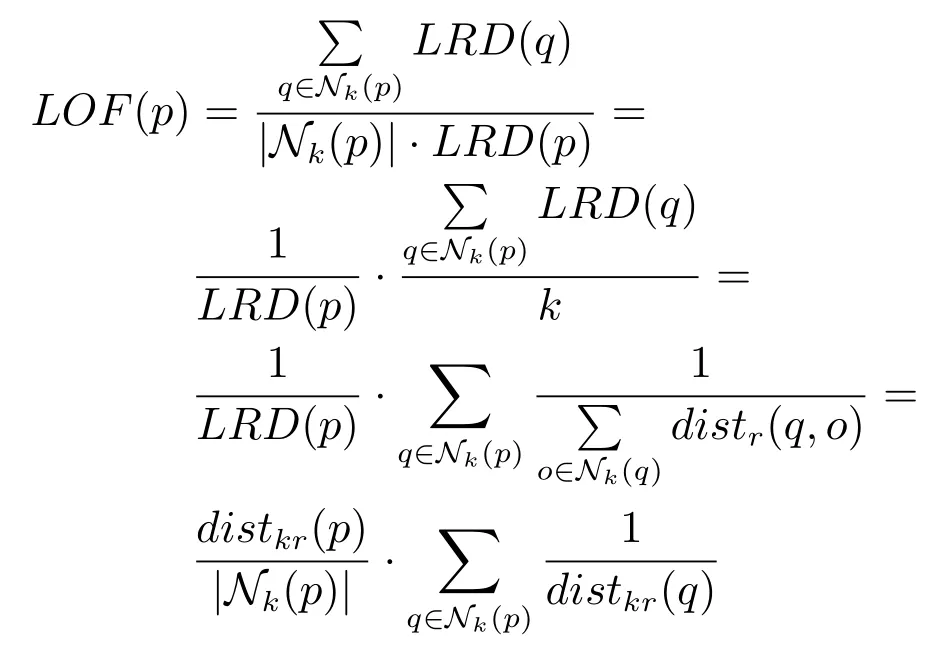
LOF(p)被表示成了两个部分的乘积,第一部分表示p的局部可达密度的倒数,第二部分表示p所有k近邻的k近邻可达距离和的倒数和.下面由定理1 引出数据对象p的第一个LOF 上界UB1(p).
定理1(LOF 的上界一).给定数据集D中的一个数据对象p,p的LOF 值满足以下上界:
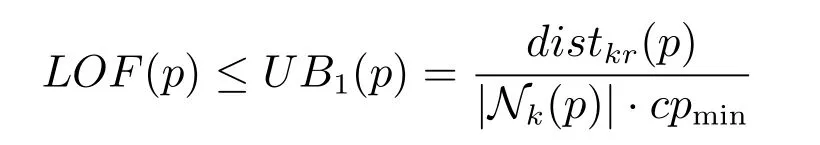
其中,cpmin表示D中所有数据对象间最小的距离.
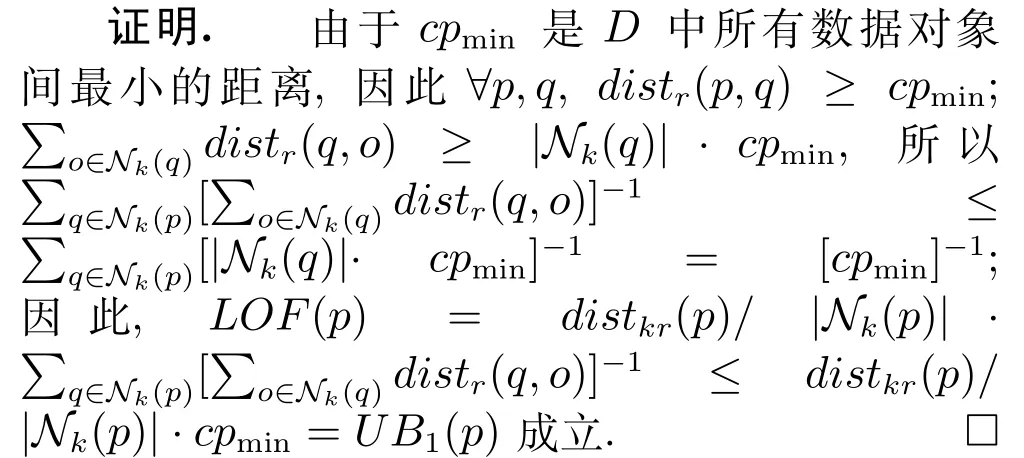
定理2(LOF 的上界二).给定数据集D中的一个数据对象p,p的LOF 值满足以下上界:
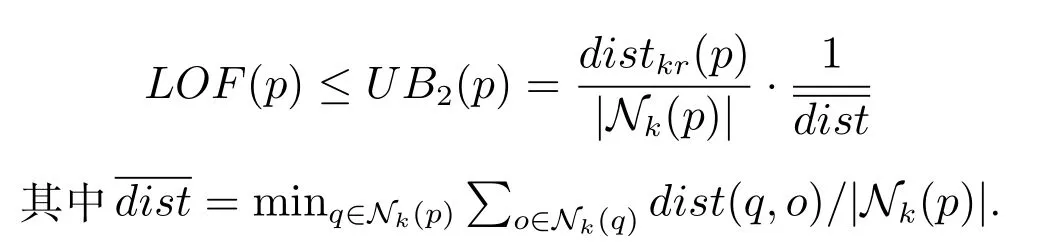

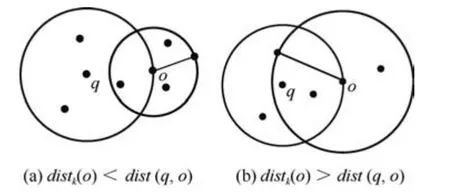
图1 distr(q,o)与dist(q,o)的关系示例Fig.1 The relationships between distr(q,o)and dist(q,o)
定理3(LOF 的上界三).给定数据集D中的一个数据对象p,p的LOF 值满足以下上界:
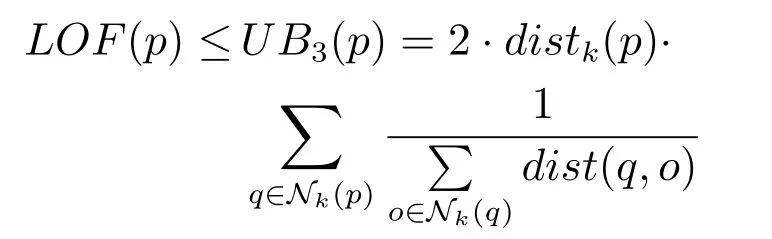
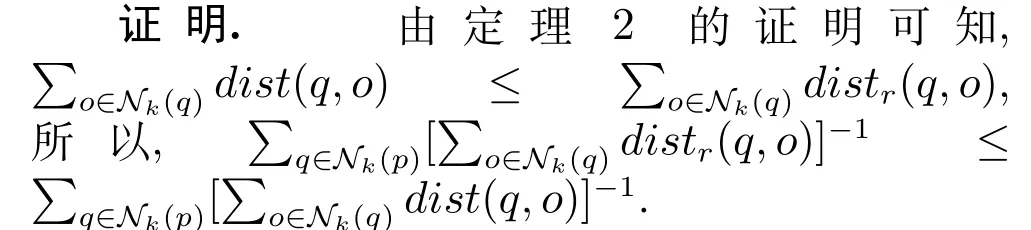
接下来只需证明distkr(p)/|Nk(p)| ≤2· distk(p)即 可.设 定directmax(p)=max{distr(p,q)|q ∈Nk(p)}[16],所以directmax(p)大于等于对象p的k近邻可达距离和的均值,即distkr(p)/|Nk(p)| ≤directmax(p),所以只需证明directmax(p)≤2·distk(p)即可.
directmax(p)是取对象p相对于它的k近邻最大的可达距离,根据定义3 可知,这等价于求解∀q ∈Nk(p),返回dist(p,q)和distk(q)的最大值,所以只需证明maxq∈Nk(p)dist(p,q)≤2·distk(p)和maxq∈Nk(p)distk(q)≤2·distk(p)即可.
由定义2 可知,∀q ∈ Nk(p),dist(p,q)≤distk(p),所以maxq∈Nk(p)dist(p,q)≤2·distk(p);对于q ∈Nk(p)来说,它的k近邻分布可分为图2(a)和图2(b)两种情况,一种情况为q附近有很多数据对象,q的k-距离小于2·distk(p),甚至小于distk(p),如图2(a)所示;另一种情况为q附近存在较少的数据对象,在最极端情况下,不存在任何数据对象,但是,当q搜索邻居的范围扩大到2·distk(p)时,一定能够涵盖p以及p的k近邻,如图2(b)所示,也就说,distk(q)≤2·distk(p).因此,maxq∈Nk(p)distk(q)≤2·distk(p).
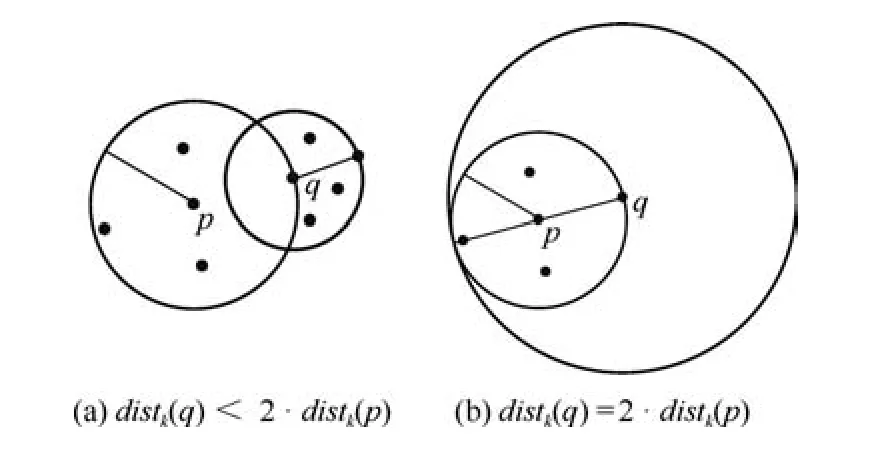
图2 distk(p)与distk(q)的关系示例Fig.2 The relationships between distk(p)and distk(q)
接下来,我们给出最后一个更加接近于LOF 值的上界UB4(p).
定理4(LOF 的上界四).给定数据集D中的一个数据对象p,p的LOF 值满足以下上界:
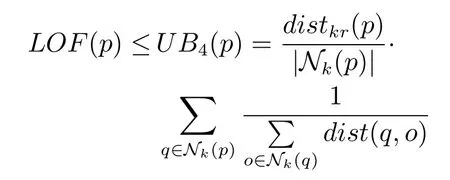

由定理3、定理4 及它们证明过程可以得出,LOF(p)≤UB4(p)≤UB3(p).
3.2.2 时间复杂度分析
根据定理1∼4,四个上界的大小顺序为:LOF(p)≤ UB4(p)≤ UB2(p)≤ UB1(p)和LOF(p)≤UB4(p)≤UB3(p).由于UB3(p)的第一部分相对于UB1(p)、UB2(p)的第一部分变大,而第二部分相对变小,因此,不能确定UB3(p)和UB1(p)、UB2(p)的相对大小.
设定数据集D中数据对象总数为N,一般情况下,,查询每个数据对象k近邻的时间复杂度为O(Nlogk),计算distkr(p)时,首先查询到p的k个近邻,时间复杂度为O(Nlogk),然后求出所有k近邻的k近邻,时间复杂度为O(k·Nlogk),求得k个可达距离并相加,时间复杂度为O(k),所以计算distkr(p)的复杂度为O[(k+1)Nlogk+k].计算时,同样,首先获得p的k近邻,然后求每个k近邻q的k近邻,并计算每个q与其近邻的距离和,时间复杂度为O[(k+1)·Nlogk+k],最后,求取k个距离和中的最小值或倒数和,时间复杂度为O(k),因此,和的时间复杂度为O((k+1)Nlogk+2k).
1)UB1(p):获取全局cpmin的时间复杂度为O(N2);但整个检测算法仅需计算一次,所以平均到每个数据对象的计算时间为O(N);计算distkr(p)的时间复杂度为O((k+1)Nlogk+k),因此,计算UB1(p)的平均复杂度为O(UB1(p))=O(N+(k+1)Nlogk+k).
2)UB2(p):根据distkr(p)和的时间复杂度知,UB2(p)的时间复杂度为O(2(k+1)Nlogk+3k).

5)LOF(p):获取distkr(p)/|Nk(p)|的复杂度为O((k+1)Nlogk+k),所以计算LRD(p)的复杂度为O((k+1)Nlogk+k+1);计算p每个k近邻q的LRD 的时间复杂度为O(k·Nlogk+k+1);因此,计算LOF(p)的时间复杂度为O((k+1)Nlogk+k+1)+k·O(k·Nlogk+k+1)+O(k)≈O((k2+k+1)Nlogk+k2+3k).
根据以上时间复杂度分析,LOF(p)的时间复杂度远大于四个上界的时间复杂度,因此,计算上界的时间远小于计算LOF 值的时间.
3.3 融合索引和LOF 上界的剪枝方法
尽管利用LOF 上界剪枝数据对象可减少计算成本,但是对于每个数据对象仍需计算k近邻可达距离和.为了快速剪枝掉高密度区域的数据对象,下面介绍融合Cell 索引和LOF 上界的剪枝方法,无需对每个数据对象进行计算即可剪枝掉高密度区域内的所有数据对象.
3.3.1 基于Cell 的全局剪枝
对于某一高密度区域内的数据对象,如果能够保证所有数据对象的LOF 值上界UBi小于临界值ct,则该区域内的所有数据对象都可以直接被剪枝掉.给定边长lenside,将整个数据空间按照lenside为单位长度划分,得到的每个子空间划分称为一个Cell,如图3 所示,包括了9 个Cell,中间Cell 记为C.
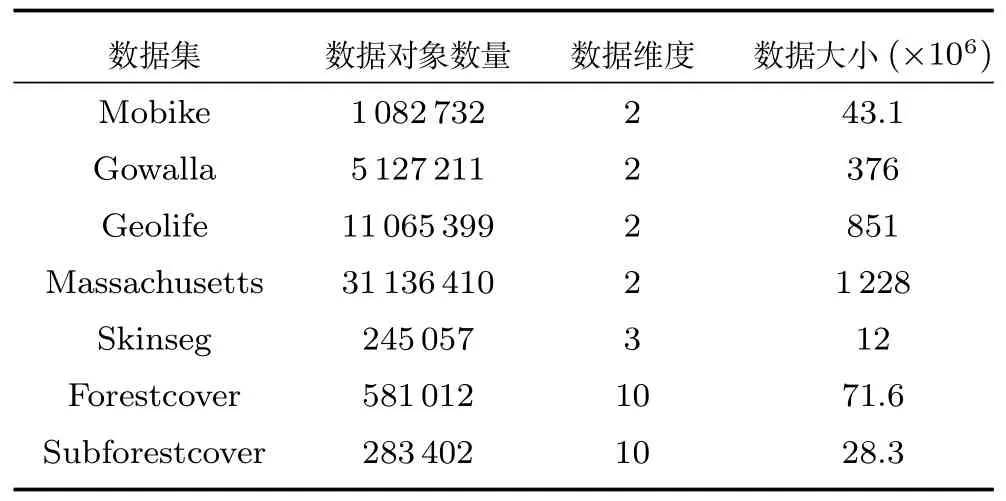
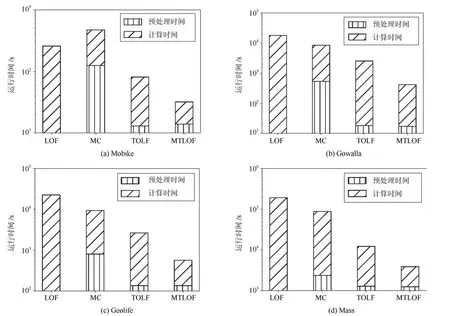
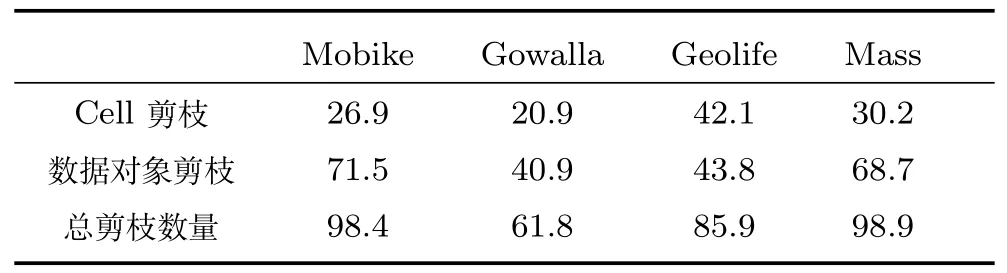
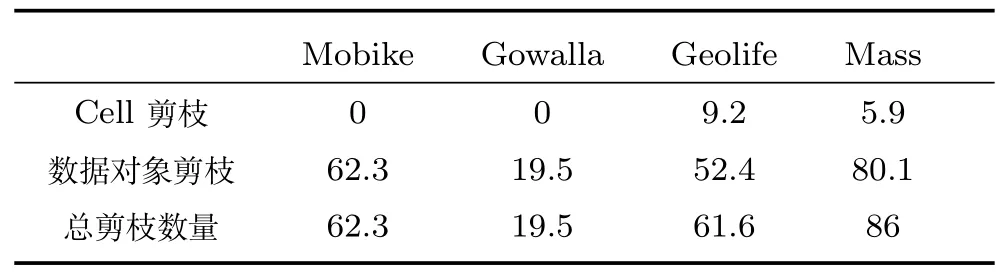
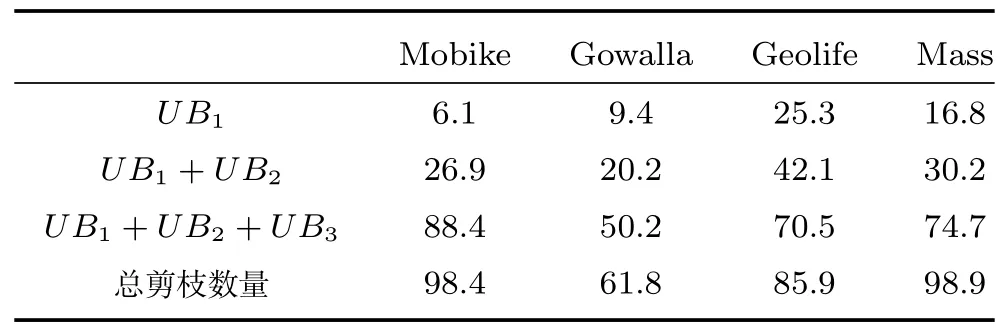
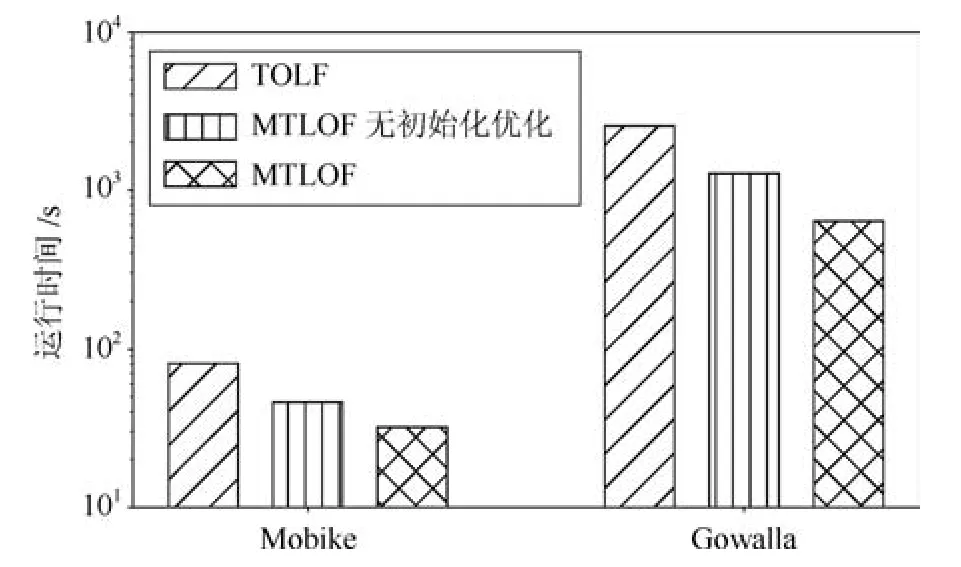
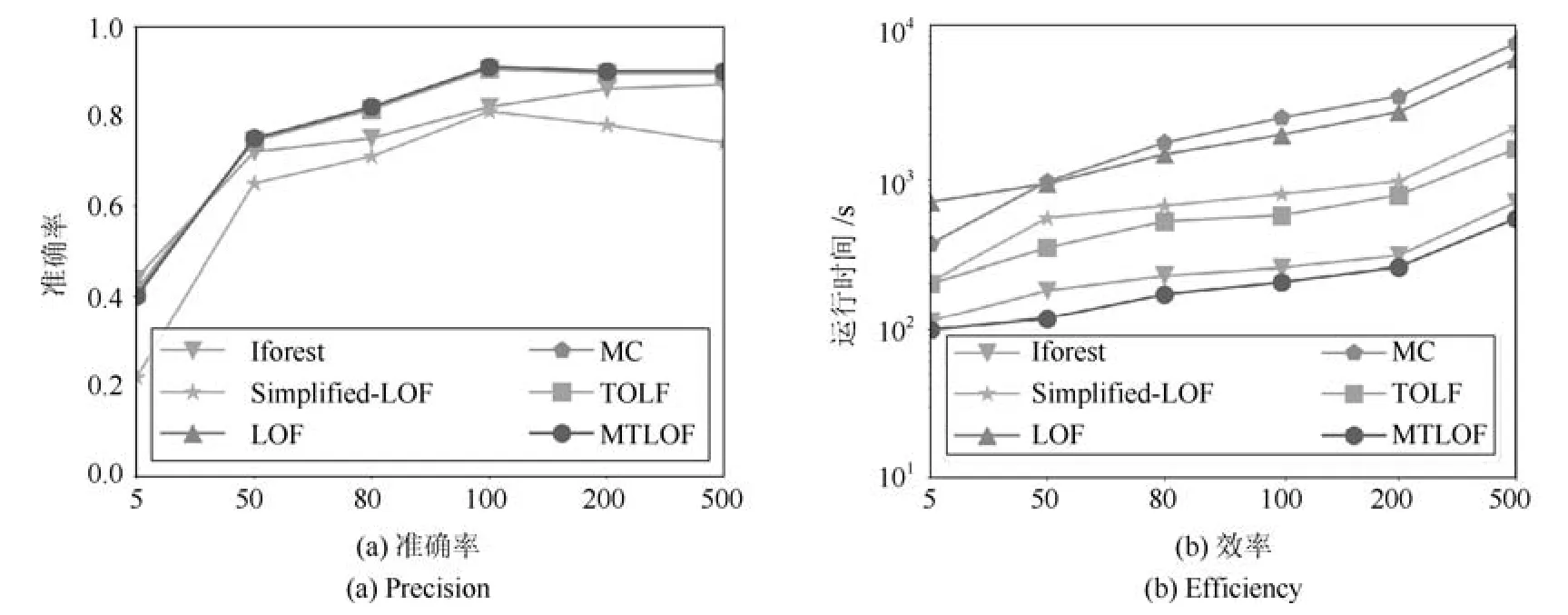
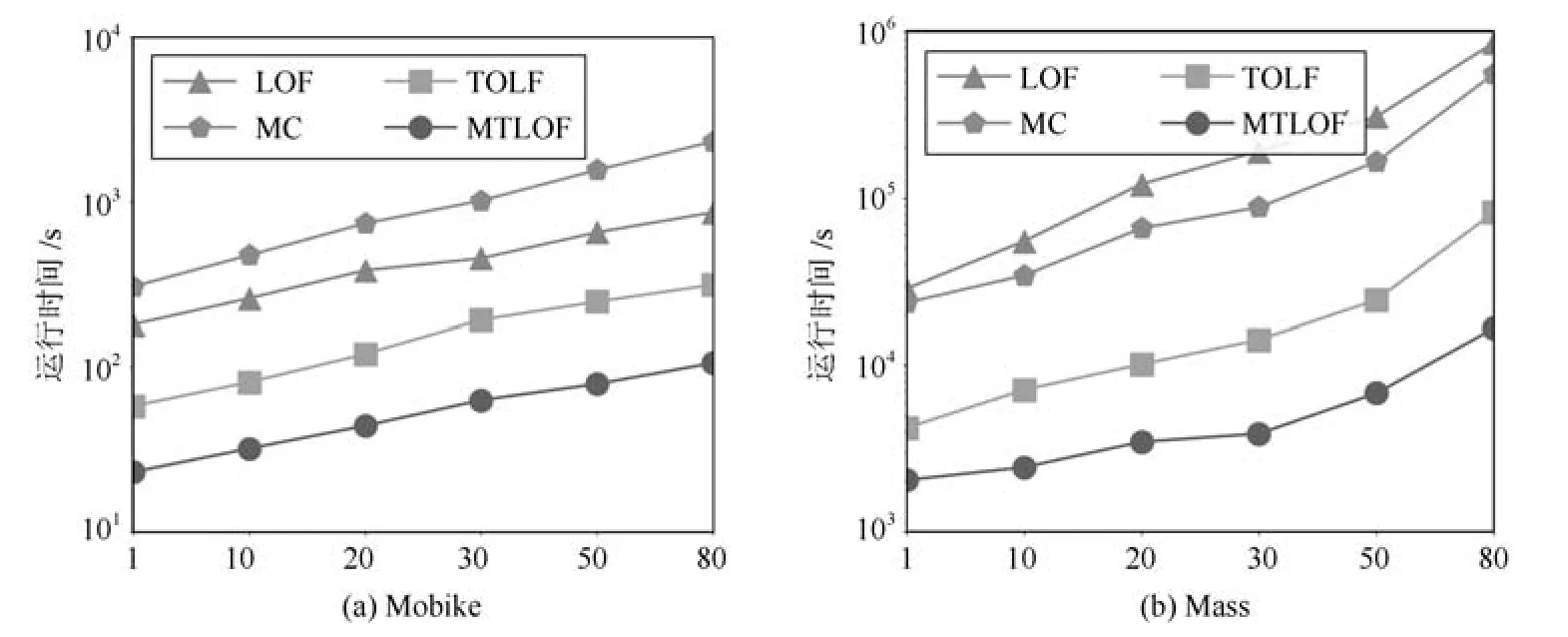
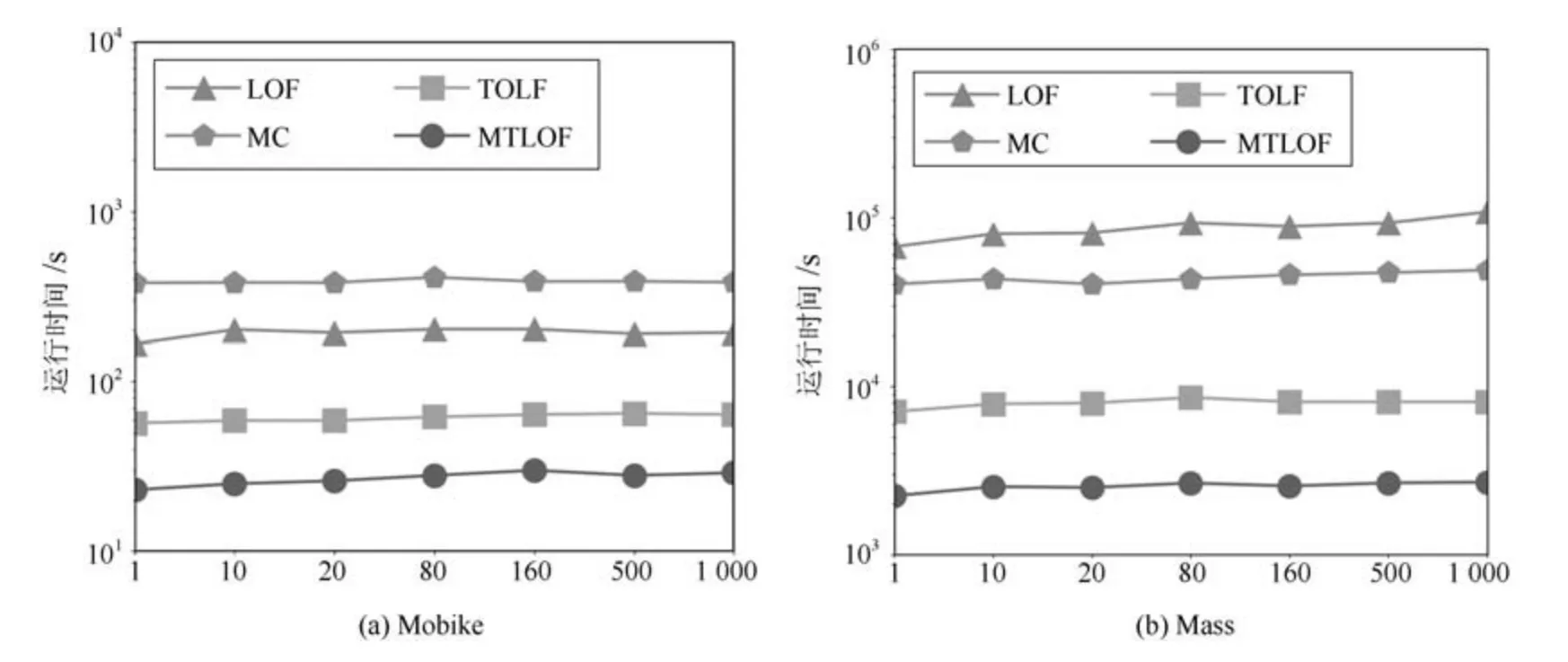
考虑使用上界UB1(p),给定一个高密度的CellC,如果对于∀p ∈C,UB1(p) 引理1(基于Cell的全局剪枝).给定一个Cell,记为C,LOF 剪枝临界值ct,如果C包含的数据对象多于k个,并且其边长(d为数据的维度),那么C中所有的数据对象可以直接被剪枝. 证明.由定理1 可知,LOF(p)≤UB1(p)=distkr(p)/|Nk(p)|·cpmin,只 需 证 明∀p ∈ C,UB1(p)≤ct即可,也就是证明distkr(p)/|Nk(p)|≤ct·cpmin. 由于C包括多于k个对象,所以对于任一对象p ∈C都可以在Cell 对角线范围内找到k近邻,即对于p的k近邻,在最坏情况下,都可以在范围内找到k近邻,即如图3 所示,当p处于C的右上角时(极端情况),假设C中仅包含k+1 个数据点,p的k近邻可能会取到C外的q点,在最坏情况下,q仍能在范围内找到k个近邻.因此, 图3 基于Cell 索引的剪枝示例Fig.3 An example of pruning based on Cell index 传统Cell 划分方法将整个数据空间按照全局的边长划分,从引理1 可知,高密度区域的剪枝条件除了与Cell 内的数据对象数量有关,还要求Cell 的边长不大于很明显,该边长条件与cpmin有关,当全局cpmin较小时,将严重影响被剪枝掉的高密度区域的数量. 基于上述考虑,本文采用文献[19]提出的均匀区域生成方法,首先将整个数据集按照数据对象分布划分成几个相对独立的数据分布相对均匀的区域,每个区域独自处理数据对象,即分区自治.具体的划分方法分为两步,1)首先将整个数据空间看成根节点,然后按照二叉树迭代地划分数据空间,直到每个叶子节点至少包括k个数据对象且不可再分;2)从叶子节点向上合并节点,如果两个子节点内部数据对象间最小的距离的大小比例小于diff,即则合并这两个子节点,直到不能再向上合并,一个独立的区域被生成.通过设定适当的比例diff,可以将两个分布相似的子节点合并,因此,可以得到相对分布均匀的区域.如图4 所示,根据数据密度分布生成4个均匀区域,每个区域内即可采用一个执行基于Cell 的全局剪枝策略. 图4 区域划分示例Fig.4 An example of area partition 虽然基于Cell 索引方法可以用于剪枝掉高密度的区域,但Cell 索引采用统一的边长划分数据空间,虽然实现简单,但是限制了大块的高密度区域的剪枝,除此之外,固定的边长也不够灵活,不便于检验不同密度的高密度区域,例如,给定边长下的某个Cell 内少于k个数据对象,但是若适当增加边长(仍满足剪枝限定条件),该Cell 即可包含多于k个数据对象.因此,本文在每个数据对象较多的区域内(|Ai| ≥t·k),建立一颗Rtree 索引,使用简单的层次索引Rtree 代替Cell 索引,Rtree 索引从上向下索引数据对象,每个叶子节点包含小于等于k个数据对象.虽然Rtree 索引的节点区域为矩形,但是可以按矩形中较长的边等同于Cell 的边长来处理,上述的引理1 依然可以适用.Rtree 索引为层次索引结构,节点的矩形大小不固定,这样,我们就可以从上向下快速剪枝掉最大块的符合边长条件的高密度区域.为了便于描述,在下文仍采用Cell 来表述Rtree 索引中的一个树节点. 3.3.2 基于Cell 的局部剪枝 从引理1 可以看出,对于被剪枝掉的Cell 需要满足全局条件虽然该方法只需计算出cpmin,但是仅考虑到上界UB1(p),忽略了Cell 内部数据对象的分布情况,下面给出考虑到Cell 内数据对象分布的局部剪枝方法. 引理2(基于Cell的局部剪枝).给定一个Cell,记为C,LOF 剪枝临界值ct,如果C包含的数据对象多于k个,并且其边长那么C中所有的数据对象可以直接被剪枝,其中 证明.与引理1 相似,只需证明∀p ∈ C,LOF(p)≤ UB2(p)≤ ct即可,也就是证明参见引理1 证明,得出 可以看出,引理1 采用了上界UB2(p)对Cell进行剪枝处理,虽然剪枝的边长条件放松了,但是该剪枝需要计算Cell 内部所有数据对象的k近邻距离和的均值.因此,本文设计了一个两层的Cell 剪枝策略,首先使用边长条件进行剪枝,若不能被剪枝掉,再使用边长条件进一步地进行剪枝判断. 经过两层Cell 的剪枝检测后,对于没有被剪枝掉的Cell,为了避免直接计算LOF 值,将首先对每个数据对象进行基于上界的剪枝判断,若不能被剪枝,再计算LOF 值,最后判断是否为Top-n异常候选项,若是,则更新临界值ct. 基于UB3(p)和UB4(p)的数据对象剪枝:根据引理1 和引理2,被剪枝的Cell 内的数据对象一般满足小于等于上界UB1(p)和UB2(p),因此,对于不满足Cell 剪枝条件的数据对象,需要采用更加小的上界来进行剪枝.根据3.2.2 节分析可知,UB4(p)≤UB2(p)≤UB1(p),UB4(p)≤UB3(p),可使用UB4(p)进一步对数据对象进行剪枝检测,但是,计算UB4(p)的时间复杂度是UB3(p)的近两倍.此外,计算每个数据对象p的UB3(p)时,可直接复用之前对该Cell 进行局部剪枝时已计算过的也就是说,可直接复用之前计算过的每个数据对象的k近邻距离和结果直接获得该Cell 内每个对象的UB3(p).因此,我们先使用上界UB3(p)对数据对象进行剪枝检测,若不满足剪枝条件,再使用更小的上界UB4(p)进行剪枝检测. 计算复用:除了计算UB3(p)时可直接复用之前的计算结果,在计算UB4(p)同样可以复用之前计算UB3(p)和时的结果.对于最终未能被上界剪枝的数据对象,在计算真实LOF 值时,也可以复用之前已经计算得到所有数据对象的k近邻和k-距离.因此,本文的检测算法对每个数据对象最多仅执行一次k近邻查询. 第3.2 节∼3.4 节详细描述第3.1 节提出的优化方法,第3.2 节回答了可利用哪些LOF 上界进行剪枝判断,而避免直接计算LOF 值,第3.3 节回答了如何结合索引技术和LOF 上界快速剪枝高密度区域内的所有数据对象,第3.3 和第3.4 节共同回答了如何使用LOF 上界,使得上界的计算尽量小,而剪枝掉的数据对象尽量多,接下来本节来回答第一个优化问题:如何快速获取到LOF 值较大的n个对象作为初始维护的候选异常对象? 初始Top-n候选异常对象的选取严重影响着检测算法的执行效率,当选择的初始数据对象的LOF值偏大时,可快速剪枝掉大量的Cell 区域或数据对象,但是,当选择的初始数据对象包括高密度区域的数据对象时,将导致初始临界值ct非常低,初始阶段将几乎没有Cell 或数据对象被剪枝.因此,在选择初始Top-n候选异常对象时应尽量避免选取高密度区域的数据对象,显然随机选择方法并不适合,因为在LOF 异常检测场景中,通常情况下异常对象是极少数的,随机选择方法更容易选取到非异常对象或高密度区域内的数据对象. 本文针对采用的区域划分和索引结构选取初始Top-n候选异常对象,Rtree 索引利用空间区域索引数据对象,每个节点记录了所包含的数据对象及覆盖的区域.对于高密度区域,通常节点包括数据对象较多,且覆盖区域较小,而局部异常点通常分散在稀疏区域.因此,本文首先在区域划分中,选择较大且数据对象较少的区域,在这些区域内随机选取初始Top-n局部异常点;如果这些区域不足n个数据对象,接着在Rtree 索引的叶子节点中,根据节点的覆盖区域,选择区域最大的个节点,在这些区域和叶子节点内部随机选取n个节点作为初始Top-n局部异常点. 本节给出本文提出的基于多粒度上界剪枝的Top-n局部异常点检测算法(Multi-granularity upper bound pruning based t op-nLOFdetection,MTLOF),MTLOF 算法的伪代码如算法1 所示. 算法1.MTLOF 算法 首先,采用均匀区域划分方法将数据空间划分成多个区域(如行1)所示),对于内部数据对象数量大于等于t·k的区域,建立一颗Rtree 索引(如行3)∼5)所示),否则,如果该区域的为SetareaSetini的最大者,将区域内的数据对象放入初始候选异常点集合Setini(如行6)∼7)所示).在数据对象较多的区域内建立Rtree 的目的有两个:一是为了进行基于Cell 的剪枝判断,二是快速查找每个数据对象的k近邻. 然后,在Setini集合中随机选择n个数据对象作为初始Top-n局部异常点,如果Setini内少于n个数据对象,则从Rtree 集合中选择覆盖区域最大的叶子节点,从中再随机选择初始Top-n局部异常点,并获取初始临界值ct,过程如行8)∼12)所示. 之后,开始遍历所有数据对象.首先遍历Setini剩余的数据对象,这是因为这些数据对象被Cell 剪枝的可能性较小.如行13)∼19)所示,首先利用上界UB3(p)和UB4(p)进行剪枝判断,若不行,再计算LOF 值,若不能被剪枝,则将p放入Topn取代LOF 值最小的数据对象,并更新临界值ct.接下来开始遍历Rtree 集合,对于每棵Rtree,从上向下遍历节点.根据引理1 和引理2,如果节点内包含多于k个数据对象,并且其边长则该节点可被剪枝掉,因此,它的所有子节点都可以被剪枝掉(行21)∼29)所示).对于不能被两层Cell剪枝策略剪枝的节点,则需要对内部每个数据对象进行基于LOF 上界的剪枝判断,如行31)∼37)所示,首先执行两层LOF 上界UB3(p)和UB4(p)的剪枝判断,若不能通过上界剪枝,再计算LOF 值,若仍大于临界值ct,则更新Topn和ct.最后,返回最终的Top-n局部异常点集合. 本节在6 个真实数据集(第4.1 节)上对所提算法进行了综合评估.首先,在第4.2 节评估了所提算法的总体效率,然后,在第4.3 节分别评估了基于Cell 剪枝和基于数据对象剪枝的效率,在第4.4节分别证明了所提的四个上界在剪枝方面的有效性以及初始化优化方法的有效性,之后,在第4.5 节评估了LOF 类算法(MTLOF、LOF、MC、TOLF)与Iforest、Simplified-LOF 算法的异常检测准确率和效率,在第4.6 节分析了参数k和n对所提的MTLOF 及对比算法的效率影响,最后,在第4.7 节验证了所提算法在多维数据集上的有效性. 实验平台采用Intel Xeon E5-2660 处理器,8核,48 GB 内存,Windows sever 2012 操作系统.所有算法采用Java 实现,MTLOF 源代码已在Github1https://github.com/LiuFang0812/TopNDetection公开. 实验数据.实验采用了6 个真实数据集,详细统计信息如表1所示. 1)Mobike:通过摩拜单车平台上2https://api.mobike.com/爬取的北京市六环内所有摩拜单车的真实Gps 位置数据,单车数量多达五万辆,该数据集仅提取了一天的数据. 2)Gowalla[35]:该数据集来自移动社交网站Gowalla,包括了19.6 万用户在2009 年2 月到2010年10 月的签到位置数据,共计644 万条位置信息,本实验提取了在北美范围内的数据,约510 万条位置信息. 表1 实验数据集统计信息Table 1 The statistical information of experimental data sets 3)Geolife[36]:该数据集来自微软亚洲研究院的Geolife 项目,收集了182 名用户在2007 年4 月至2012 年8 月间的Gps 轨迹数据,每条Gps 轨迹由带有时间戳的经纬度位置点序列组成. 4)Massachusetts(Mass)[37]:该数据集通过Openstreemap3https://www.openstreetmap.org采集,在美国马萨诸塞州范围内所有的建筑物的地理位置,数据集中的每一行代表一栋建筑物,地理位置采用经度和纬度两个属性表示. 5)Skinseg[38]:该数据集从不同年龄组(青年、中年、老年)、不同种族(白人、黑人、亚洲人)以及不同性别的人脸照片中随机采样的B、G、R 数值的数据集,包含三维特征属性. 6)Forestcover[39]:该数据集来自科罗拉多北部罗斯福国家森林的四个荒野森林(Neota、Rawah、Comanche Peak 和Cache La Poudre),共包括58 万多个30×30 平方米的区域,每个区域包含了各种树种的海拔高度、数量以及坡度等十个属性. 7)Subforestcover[39]:该数据集选取了Forestcover 数据集中所有带标签的数据,共包括28 万多个对象.Rawah 和Comanche Peak 森林主要生长的物种为黑松,它们的物种和特征变量的范围(如海拔范围等)都比较典型,于是把标记为黑松的数据记录视为正常对象,标记类别为2,Cache La Poudre森林主要生长黄松、花旗松和杨木/柳树,由于相对较低的海拔和物种组成,该森林相比其他森林更为独特,数据集中将标记为杨木/柳树的数据记录视为异常对象,类别标记为4,异常对象数量的比例为Subforestcover 数据的7%. 对比算法.为了验证所提MTLOF 算法的有效性,实验结果与LOF 算法[16]、MC 算法[20]以及最新的TOLF 算法[19]、Iforest 算法[33−34]、Simplified-LOF[28−29]进行了对比分析. 评估指标.针对算法的效率评估,测量了每个算法总的检测时间,同时还分别测量了数据预处理和检测计算的CPU 时间.为了更好地评估算法性能,实验部分还对算法的剪枝效果进行了评价. 首先,在表1 所示的四个二维数据集上,评估了我们提出的MTLOF 的效率,并与LOF、MC、TOLF 算法进行了对比分析. 实验结果如图5 所示,参数n取0.001%·|D|,由于各数据集的数据对象数量及分布不同,在Mobike、Gowalla、Geolife 和Mass 数据集,k分别取6、20、20 和30,与TOLF 算法设置一致,固定diff为10,t为6. 从图5 可以看出,MTLOF 算法在四个数据集上都表现出了最好的检测效率,相比LOF、MC 和TOLF 算法,分别平均提升了30、18 和2.6 倍的效率.特别是在大规模的Geolife 数据集,相比最新的TOLF,MTLOF 算法提升的效率高达3.5 倍.MTLOF 和TOLF 都采用了均匀区域划分的预处理方法,还对区域内数据对象建立了索引结构,极大地加快了k近邻的搜索,减少了数据预处理的时间.虽然MC 算法也通过聚类的方法对数据进行预处理,在聚类结果上进行相应的剪枝,但是数据对象聚类所消耗的预处理时间远高于建立索引的预处理时间.最新的TOLF 在划分的区域内建立Cell 网格索引,利用cpmin进行一次Cell 剪枝,然后利用较大的两个上界进行两次数据点剪枝,然而当区域内的cpmin较小时,几乎没有Cell 被剪枝掉,而且执行数据点剪枝的两个上界相比真实LOF 值较大且计算量较高.而本文所提的MTLOF 采用了两层Cell 剪枝策略,除了使用全局的cpmin剪枝,还利用基于Cell 内部数据对象分布的局部剪枝策略,当cpmin较小时,仍能通过剪枝掉高密度的Cell,此外,我们使用层次的Rtree 代替Cell 网格索引,可以更快速地剪枝掉较大块的高密度节点.对于不能被剪枝的节点内的数据对象,我们采用了两个更加接近LOF 值的上界进行剪枝判断,从而使得被剪枝掉的数据对象更多,同时,基于我们的复用计算优化,对UB3(p)和UB4(p)的计算完全可复用Cell 剪枝过程中的计算,有效减少了检测计算成本.MTLOF 效率远高于TOLF 的另外一个重要原因还在于,我们优化了对初始局部异常点的选取,利用预处理过程的区域划分和数据索引,优先在稀疏区域和Rtree 中覆盖区域较大的叶子节点内部选择初始候选局部异常点,相比随机选择方法,大大提升了初始异常点的LOF值,相应地,也提升了初始临界值ct,使得更多的树节点在初始阶段被快速剪枝. 图5 总体效率对比评估Fig.5 Comparison evaluation of overall efficiency 为了验证算法剪枝的有效性,在上一个实验的同时,我们还在四个数据集上统计了MTLOF 和TOLF 算法的Cell 剪枝及对象剪枝中被剪枝的数据对象数量.MTLOF 算法的统计结果如表2 所示,TOLF 算法的统计结果如表3 所示. 表2 MTLOF 剪枝数量(%)Table 2 The pruning number of MTLOF(%) 表3 TOLF 剪枝数量(%)Table 3 The pruning number of TOLF(%) 从表2 和表3 可以看到,在四个数据集上,MTLOF 的总剪枝的数据对象数量都远多于TOLF 的总剪枝数量.在Mobike 和Mass 数据集上,MTLOF 算法直接剪枝掉的数据对象总量高达98% 以上,在TOLF 剪枝较少的Gowalla 数据集上,MTLOF 也直接剪枝了61.8% 的数据对象.更为明显地是,MTLOF 的Cell 剪枝的数据量比例都在20%以上,甚至高达40% 以上,而TOLF 的Cell 剪枝比例相对较少,在Mobike 和Gowalla 数据集上,TOLF 的Cell 剪枝甚至为0%,这是因为在Mobike和Gowalla 数据集的高密度区域内,数据对象间的最小距离往往非常小甚至为零,在TOLF 的Cell 剪枝中,始终采用为Cell 边长,当每个区域的cpmin都很小时,就使得Cell 剪枝失效.而本文所提的MTLOF 除了基于Cell 的全局剪枝,还引入了基于Cell 的局部剪枝,当区域内的cpmin较小时,仍能通过每个节点(Cell)内数据对象的进行Cell 剪枝.此外,在同一数据集上,MTLOF的数据对象剪枝的数量比例也高于TOLF 的数据对象剪枝比例,这是因为MTLOF 采用的两个上界UB3(p)和UB4(p)更加接近于真实LOF 值,因此,被剪枝掉的数据对象更多,这也说明了本文所提的LOF 上界更加合理有效.优化的初始局部异常点选择方法也是MTLOF 算法具有较高的剪枝比例的重要原因,初始临界值ct越高,被剪枝掉Cell 和数据对象数量也就越多. 为了评估UB1、UB2、UB3和UB4四个上界在剪枝方面的有效性,本节在四个二维数据集上,分别统计了UB1、UB1+UB2、UB1+UB2+UB3和UB1+UB2+UB3+UB4四种组合情况下的被剪枝的对象数量,实验结果如表4 所示.第二行表示在每个数据集上仅利用上界UB1剪枝的对象数量,第三行表示同时采用UB1和UB2剪枝的对象数量,第四行表示通过UB1、UB2和UB3总共剪枝的对象数量,最后一行表示同时使用四个上界时的总剪枝数量.可以看到,随着采用上界个数的增加,表中每行剪枝数量比例都有所增加,这证明了每个上界剪枝都是有效的.利用上界UB1的Cell 全局剪枝,虽然计算成本较小,但是剪枝的数量也相对有限.基于UB2的Cell 局部剪枝,虽然需要计算本地所有数据对象的k近邻距离和的均值,但剪枝掉的数量也相对较多.上界UB3和UB4主要用于剪枝Cell 过程中未被剪枝的对象.根据第3.2.2 节分析可知,UB4(p) 此外,我们还在Mobike 和Gowalla 数据集上统计了MTLOF 在采用初始Top-n异常对象优化选取方法和没有采用优化选取方法时分别所需的运行时间,实验结果如图6 所示.相比TOLF 算法,没有采用初始化优化方法的MTLOF 在两个数据集上分别提升2.1 和2.5 倍,而采用初始化优化的MTLOF 分别提升2.6 和3.4 倍.也就是说,本文所提的剪枝策略在两个数据集上提升2.1 和2.5 倍效率,而初始化优化方法又进一步提升1.3 倍和1.4倍. 表4 MTLOF 每个上界剪枝数量(%)Table 4 The pruning number of each upper bound in MTLOF(%) 图6 初始化优化方法有效性评估Fig.6 Effectiveness evaluation of initialization optimization 本节在Subforestcover 数据集上评估了MTLOF 算法以及对比算法LOF、MC、TOLF、Iforest、Simplified-LOF 的准确率和效率.准确率=(R ∩D)/R,其中D表示数据集中真实的异常对象集合,R指检测算法发现的异常对象集合. 实验结果如图7 所示,对于MTLOF、LOF、MC、TOLF 和Simplified-LOF 算法,横坐标表示参数k值,对于Iforest 算法,横坐标表示为训练Itree 而采样的对象子集数量m.图7(a)展示了所有算法检测结果的准确率,由于MTLOF、MC 和TOLF 都是通过计算对象的LOF 值来检查Top-n异常的,所以这三种算法的准确率与LOF 算法一致,同时,实验结果也验证了本文所提剪枝策略的正确性.从图中还可以看出,LOF 类算法(MTLOF、LOF、MC、TOLF)的准确率在k(m)≥50以后一直优于Iforest 和Simplified-LOF 算法.当k取100 时,LOF 类算法的准确率达到最大的93%.而对于Iforest 算法,准确率最高仅达到86%.Simplified-LOF 算法的准确率相对小,最大值仅达到81%,之后不断增大k值,准确率反而急剧下降,这是因为Simplified-LOF 直接用k-距离代替可达距离,当k值较大时,采用k-距离所表示的局部密度将变的不准确. 图7(b)展示了所有算法在参数变化下的检测时间,可以发现,MTLOF 的运行时间一直优于所有对比算法.随着k(m)值增加,所有算法所需的运行时间都有所增加,这是因为随着k的不断增大,搜索k近邻的时间不断增加.尽管如此,MTLOF 在所有测试参数下的运行时间都少于Iforest 所消耗的时间.MTLOF 相比Simplified-LOF 和Iforest 算法,平均分别提升3.7 和1.5 倍效率. 本节在Mobike 和Mass 数据集上评估重要参数k和n的变化对所提MTLOF 算法以及对比算法的效率影响. 图7 准确率和效率评估Fig.7 Evaluation of precision and efficiency 4.6.1 参数k 影响评估 固定参数n=0.001%·|D|,从1 到80 变化参数k,图8 展示了四个算法在两个数据集上随着参数k变化的总检测时间.如图8 所示,MTLOF的检测效率在两个数据集上的所有测试都一直优于三个对比算法,相比LOF、MC 和TOLF 算法分别平均提升了28,19 和2.7 倍.随着k值的增大,所有算法消耗的总检测时间越来越长,这是因为k值的增加,使得所有数据对象的k近邻查询越来越费时,导致总处理时间直线增加.尽管如此,随着参数k的增加,MTLOF 比LOF、MC 和TOLF 算法节省的CPU 时间越来越多,优势越来越明显,这是因为k值的增加使得Rtree 索引的叶子节点不断增大,同时所提的上界也更加接近于真实的LOF 值,致使MTLOF 剪枝掉更多的节点和数据对象,相对对比算法,效率优势越来越明显. 4.6.2 参数n 影响评估 图9 展示了算法随参数n变化的总检测时间,在Mobike 数据集上固定k=5,在Mass 数据集上固定k=10,从1 到1 000 变化参数n.如图9 所示,MTLOF 算法在所有参数下的检测效率都优于三个对比算法,相比最新的TOLF 算法,平均提升了2.75 倍.所有算法的检测时间相对于n的变化并不明显.基本的LOF 算法检测Top-n局部异常分为两个步骤,首先计算所有数据对象的LOF 值,然后排序获取前n个异常对象,随着n的不断变化,排序所花费的时间也会不断地增加,但是这个排序的时间相比计算LOF 的时间要小的多,使得总的检测时间并没有明显增加.MC 算法首先采用Birch聚类获得聚类簇,然后按照聚簇的半径和距离关系排序聚类簇,仅需在最可能包含异常的簇内检测异常,因此,随着n的增加,需要检测的聚簇个数越多,消耗的总检测时间也越长,但是MC 在n较小时剪枝掉的数据数量都相对较少,因此,总消耗的检测时间也没有明显增加.TOLF 和MTLOF 算法的检测时间随着n的增加而缓慢增加,这是因为n的增加使得初始需要计算LOF 值的数据对象增加,尽管如此,由于两个算法都对数据进行了均匀区域划分并在区域内建立了索引结构,即使n不断增加,仍然可以通过索引快速查找k近邻,并通过LOF 上界执行剪枝,因此,总检测时间也没有急剧增加.随着n的增加,我们MTLOF 能够通过提出的UB3(p)和UB4(p)上界剪枝掉更多数据对象,相比TOLF,节省更多检测时间. 图8 参数k对检测时间的影响Fig.8 Impact of parameter kon detection time 图9 参数n对检测时间的影响Fig.9 Impact of parameter non detection time 图10 多维数据集上的效率评估Fig.10 Efficient evaluation on multi-dimensional datasets 最后,在多维数据集Skinseg 和Forestcover 上评估了所提算法的有效性.图10 展示了四个算法在Skinseg 和Forestcover 上的总检测时间.参数n固定为0.001%·|D|,k固定为6.在Skinseg 数据集上,MTLOF 仍然能比最新的TOLF 算法快了近2.5 倍.虽然Skinseg 数据集较小,但本文提出的多粒度的剪枝策略在这个数据集上明显优于TOLF 算法.在10 维的Forestcover 数据集上,MTLOF 算法也展现了所提剪枝策略的优势,相比LOF、MC和TOLF 算法分别提升了15 倍、12 倍和3 倍的检测效率,这也说明了MTLOF 在高维数据集上具有更高的可扩展性. 本文提出了一个面向大数据的高效的Top-n局部异常点检测算法MTLOF.首先,为了避免直接计算数据对象的LOF 值,提出了四个计算复杂度更低并且更接近于真实LOF 值的上界.其次,结合索引结构和LOF 上界,引入了两层的Cell 剪枝策略.然后,针对未被剪枝的Cell 内部数据对象,利用UB3(p)和UB4(p)上界提出了两个更加合理有效的剪枝策略.此外,还利用均匀区域划分和建立的索引结构,优化了初始候选局部异常点的选取方法,使得LOF 值较大的数据对象被选取为初始局部异常点.最后,在六个真实数据集上的综合实验评估验证了所提MTLOF 算法的有效性,相比LOF、MC 和TOLF 算法,检测效率可分别提升30、18 和2.6 倍. 下一步工作将考虑借助分布式计算平台,设计分布式异常检测算法以进一步提升检测效率,此外,还计划面向不断快速增长的海量高速数据集,研究实时的Top-n局部异常点检测方法.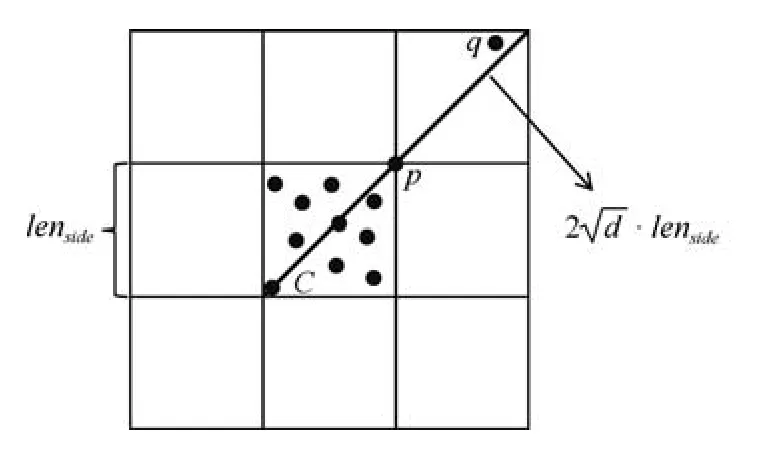
3.4 基于LOF 上界的数据对象剪枝
3.5 选取初始候选局部异常点
3.6 MTLOF:Top-n局部异常点检测算法

4 实验评估
4.1 实验数据与测试方法
4.2 总体效率评估
4.3 剪枝效率评估
4.4 优化有效性评估
4.5 正确性评估
4.6 参数敏感性分析
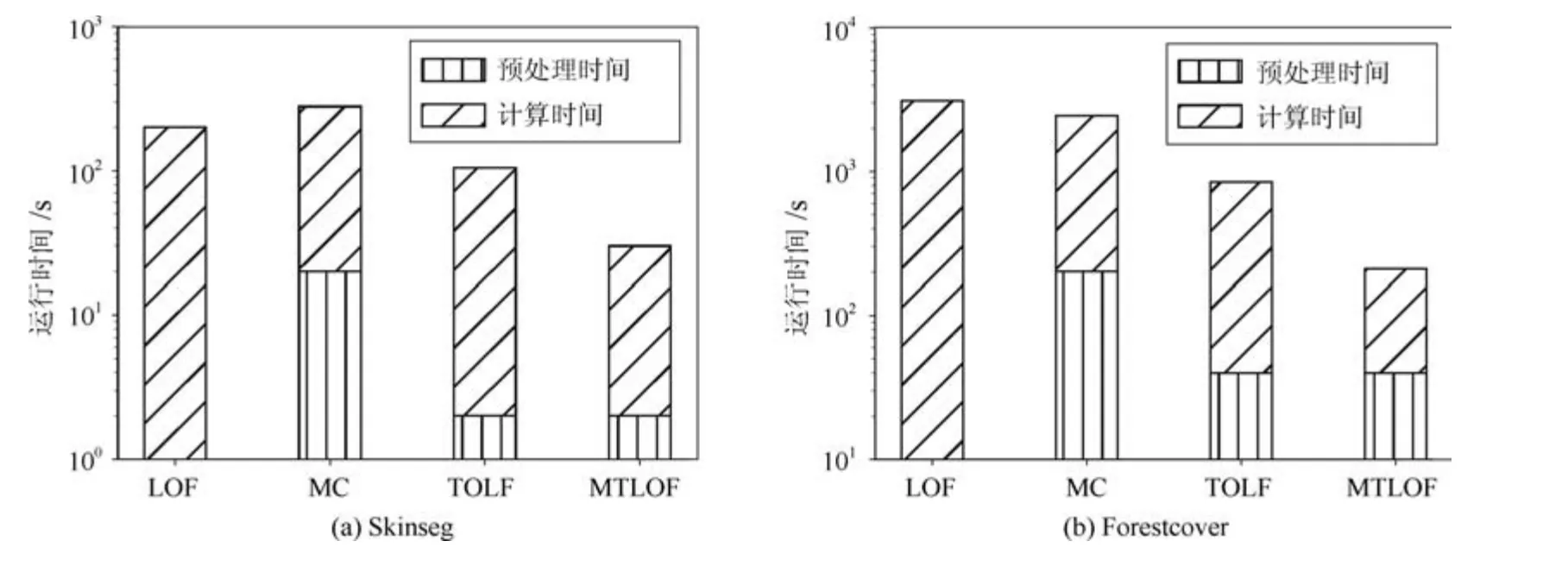
4.7 多维数据上的有效性评估
5 结论
