从项目式学习与配对编程到跨学科综合设计*——基于2006-2019年国际K-12 计算思维研究的元分析

马志强 刘亚琴

（江南大学 教育信息化研究中心，江苏无锡 214122）

一、研究背景

伴随着信息技术的迅猛发展， 众多国家及地区开始关注学生计算思维的发展。 许多国家已将计算思维纳入到K-12 课程体系中， 将其列为国家项目或编写进新教材。 如，2014年，以色列、新西兰、澳大利亚、丹麦以及德国的部分州，将计算思维培养的相关课程纳入到高中计算机科学的课程大纲中[1]；2016年1月，美国启动了“人人享有计算机科学”计划[2]；我国在高中信息技术课程标准的重修中， 也将计算思维列为信息技术课程的核心素养之一。

计算思维在K-12 教育中的发展，可追溯到麻省理工学院西摩·佩伯特（Papert S.A.）教授通过LOGO编程，发展儿童程序化思维的理念与实践[3]。 “计算思维是通过运用计算机科学的基本概念解决问题、设计系统和理解人类行为的基本技能”[4]， 它作为一个专业术语，则是由计算机科学家周以真于2006年首次提出。

关于计算思维的定义，可从广义与狭义两个角度进行理解。 从广义上讲，计算思维是分析和解决各种问题的基础[5]。 计算思维不应局限于计算机编程学习，而应像阅读、写作能力一样，是每个人日常生活的必备技能之一[6-7]。 计算思维可在编程以外的领域（科学、社会科学、人文等）进行迁移[8-9]，能够与各种学科知识内容相结合[10]，比如，英语[11-12]、艺术[13]、生物[14-15]、数学等[16]。 从狭义上讲，计算思维是基于计算机编程的一系列概念，是开始编程前的思考过程，是将编程解决方案的思路转换成计算机能够操作执行的计算机语言的过程。 综上，计算思维的本质可以理解为:概念的抽象与问题解决，是借助计算机等工具进行抽象表征以寻求问题解决最优化方案的思维过程。

从K-12 计算思维发展的角度讲， 概念抽象与问题解决是中小学生难以理解的，因此，需要搭建跨学科的问题解决平台，综合采用多种教学方法，将抽象的概念及思维过程， 转化为中小学生能够理解的具体知识内容[17-18]。目前，主要有两种主流路径:一是借助可视化编程工具， 采用编程教学进行计算思维的外化表征[19-20]。然而，有学者认为，这种可视化编程路径可能会限制学生的逻辑思维潜力[21]。 另一种路径强调结合具体学科内容， 设计跨学科课程来发展计算思维。 然而，跨学科融合的复杂性，使得教学方法选取及研究方案设计颇具挑战性。 如，Berland 与Wilensk 在一项编程与物理结合的课程研究中指出，同时教授学生计算机编程和复杂系统的内容， 较难选择教学方法，可能会使内容太多、教得太快，使学生难以适应[22]。

从研究设计来看， 跨学科教学涉及大量研究变量的控制及研究工具的选择， 研究者需要具备较强的研究设计能力。 鉴于此，计算思维领域的研究者，迫切需要了解哪些教学方法及研究设计要素， 能够显著影响计算思维的发展。基于此，本研究采用元分析的方法，选取2006年至今13年内的33 项国际高水平实验、 准实验计算思维研究成果， 进行整合分析， 旨在对比分析不同类型教学方法及研究设计方案，对计算思维发展的影响，从而为后续研究者与实践者，提供教学方法选择以及研究方案设计的依据。

二、文献综述

结合研究目标， 文献综述主要聚焦于计算思维发展的评价维度、教学方法以及研究设计三个部分。

众多研究者都提出，计算思维可以从学业成就、思维技能以及合作关系等角度进行评价。 学业成就包括编程成绩、学科成绩、项目绩效等。其中，编程成绩主要指序列、循环、并行性、事件、条件、运算符等具体概念的应用水平[23-24]，如，Wang 等根据学生的编程作品评价条件、循环逻辑等编程知识[25]。 学科成绩是对计算思维跨学科培养所整合的学科知识进行评价。 项目绩效是指对具体学科（如，物理、数学等）所涉及到的相关任务或活动成果进行评价[26]。思维技能通常利用计算思维发展所必备的问题解决思维[27-28]、算法思维[29]、批判性思维[30]等相关思维能力来表征。合作关系也是计算思维评价的重要维度， 如，Korkmaz 等将合作关系纳入计算思维评测量表中，开发了由创造力、合作、算法思维、批判性思维和解决问题思维组成的计算思维评价量表[31]；钟柏昌等也将小组合作关系作为计算思维发展的重要目标[32-33]。

K-12 计算思维发展的教学方法设计主要从三个角度出发:一是从计算思维的可视化表征出发，设计多样化的计算思维表征方法， 如， 基于游戏的学习、项目式学习等。 例如，Yang 和Chang 的实证研究将枯燥的代码转变为数字游戏的可视化输出， 提高了学生的注意力和参与度， 促进了批判性思维的发展[34]；Webb 引导中学女生使用Alice 编程工具，来完成半结构化的交互式故事， 提升了学习兴趣与计算思维[35]。 二是从计算思维的问题解决本质出发，如，设计问题驱动的教学方法，例如，Hsu 和Hwang 建立了一个问题驱动的学习环境， 帮助学生学习编程概念[36]。 三是从合作角度出发，设计配对编程或小组合作教学法， 通过合作编程的方法发展学生的编程知识和思维技能[37]。

从上述分析来看， 大量不同类型的教学方法被用于发展计算思维。 Hsu 等对2006年到2017年的120 篇计算思维实证研究文章进行了内容分析，梳理出基于问题的学习、 项目式学习等16 种教学方法，并指出:基于问题的学习与项目式学习对于指导K-12 计算思维能力的发展、学习成绩的提高，较为有效。 然而，Hsu 仅仅进行了初步的内容分析，后续研究者仍需要通过严谨的量化分析方法， 来比较不同教学方法对计算思维的影响[38]。

关于计算思维发展的研究设计， 研究者主要关注样本规模、学段、应用学科、研究时长等设计要素。针对样本规模，研究者会选取不同规模的研究对象，如，Miller 分析了一位听力障碍学生使用Logo 语言学习英语单词[39]；Dura 则选用110 名五年级学生进行不同编程工具应用效果的准实验研究[40]。 关于研究学段，主要集中在小学，也有少量研究涉及中学与幼儿园[41]。 如，Wyeth 采用简单任务帮助幼儿园学生理解电子积木的功能与编程概念[42]；Kahn 等将小学数学与编程结合， 采用Toontalk 编程工具将数学概念具体化[43]。 关于应用学科，主要集中在计算机编程，也有英语、数学、物理等跨学科的课程涉及。 如，在语言学习中，Burke 利用Scratch 来发展学生的写作技能[44]。 在研究时长方面，研究者设计不同的时长方案，如，Wang 等持续六周分析学生学习Flash Action-Script 的情况[45]；Fessakis 则仅仅选取了45 分钟的时长来分析幼儿园儿童使用LOGO 编程工具的思维变化情况[46]。 综上所述，样本量大小、学段情况、应用学科、 研究时长是计算思维发展研究设计的要点，然而，它们对计算思维发展的影响尚待进一步考察。

三、研究过程与方法

我们以国际范围内计算思维发展的高水平定量研究成果为分析对象， 全面整体分析国际K-12 计算思维教学的作用效果、 教学方法及研究设计对计算思维发展的影响，具体研究问题为:（1）计算思维教学的总体作用效果如何？在学业成就、思维技能与合作关系三个维度的具体效果如何？（2）计算思维发展的各类教学方法应用效果如何？（3）计算思维发展的研究设计（研究样本量、研究学段、研究时长、学科）的影响效果如何？

我们采用一种依据单项研究数据进行定量综合的分析方法——元分析， 对国外K-12 计算思维的实验与准实验研究进行系统分析。 元分析也叫Meta分析、荟萃分析，是对具有相同研究目的的多个独立研究结果进行系统、 定量、 综合分析的一种研究方法， 其特点在于依靠实证研究数据来精确反映已有研究设计的有效性[47]。 元分析实施的基本流程包括:确定主题并检索文献、制定筛选标准并选取文献、确立编码文献特征值并分析数据。首先，全面检索并确定与主题相关的实证研究范围；其次，综合建立文献筛选标准并据此选取文献， 这一步骤需要研究者对已有单项研究进行详细分析与整体把握， 严格选取原始文献；最后，根据研究问题对文献特征值进行归类编码并对原始数据进行统一分析。 本研究选取Rev Man 5.3 软件辅助进行文献元分析。

（一）文献检索

选取Science Direct 数据库、Web of Science 核心合集中的“科学引文索引（扩展版）”（Science Citation Index Expanded，SCI-EXPANDED）、“社会科学引文索引”（ Social Sciences Citation Index， SSCI）以及ProQuest 硕博论文数据库等三个数据库作为数据来源。由于“计算思维”这一专业术语最早于2006年提出， 故本研究文献检索的年限设定为2006年1月-2019年4月，共经过三轮检索:

第一轮，分别使用三个数据库的高级检索功能，以“computational thinking”作为主题词进行检索，检索出241 篇文献。

第二轮， 分别使用三个数据库的高级检索功能，分别以“computer programming”、“pair programming”和“experiment”作为主题词进行高级检索，检索出160 篇文献。值得一提的是，本研究的目的是综述有关计算思维的文章，而“计算机编程”是发展计算思维的首要切入点。 因此，在第二轮检索中，使用了“computer programming”作为主题词。

第三轮，采取“滚雪球”的检索方式，即从已检索到的文献、 相关计算思维的综述类文献所引用的参考文献中，进行二次检索，共获取37 篇随机实验或准实验类文献。

（二）文献筛选标准

（1）研究主题:K-12 计算思维发展；（2）研究类型:实验研究，包括随机实验和准实验，其中，单组实验需要有前后测的对照， 双组实验应有实验组和对照组；（3）研究环境:正式课堂教学或非正式的课外教学研究环境；（4）研究对象:K-12 学段的学生；（5）结果指标: 学业成就类、 思维技能类以及合作关系类；（6）研究数据:研究数据须清晰完整，如，平均值（MD）、标准差（SD）等，可进行平均效应值与合并效应值的计算。

（三）文献编码

如图1 所示，为保证数据筛选的信效度，共有两位研究者分别对初筛的101 篇文献进行独立复筛，并一一核对，若有分歧则通过讨论解决。 最终，有28篇文献可纳入本研究的元分析中， 共有35 个效应值，其中，有五项研究（如，wang.et al、Fadjo、Kim.et al、Sengupta.et al、Atmatzidou.et al）涉及到两个独立实验或准实验，各算为两项研究，因此，纳入分析的共计有33 项研究。

图1 文献筛选流程与结果呈现图

为便于后续分析， 本研究根据自制的文献特征值编码表进行资料提取，从而为元分析做准备。资料提取主要内容有六项:（1）纳入文献的基本信息，包括第一作者、出版年份、期刊来源等；（2）研究设计的基本情况，包括研究样本大小、学段情况、持续时间、研究学科；（3）使用的教学方法，包括项目式学习、基于问题的学习等；（4）研究的作用效果，包括学业成就类、思维技能类与合作关系类；（5）实验结果，包括积极、中性和消极结果；（6）文献来源。最终得到的编码列表如表1 所示。

根据所得到的编码列表进行归类， 研究样本量分为三种规模: 小规模为100 人以内， 中等规模为100 到200 人，大规模为200 人以上；研究学段分为两类:小学为1-6年级，中学为7-12年级；研究时长分为三个时间段:2 周以内、2 周到8 周、8 周以上；研究学科包括计算机编程、数学、生物、科学等。

表1 元分析文献编码列表

注：在实验样本列中，前一数值为实验组人数，后一数值为对照组人数。

（四）发表偏倚评价

“发表偏倚”是指由于研究者、审稿者以及编辑在选择论文发表时，依赖研究结果的方向与强度所产生的偏差。 即出版有一定的选择性，研究所得若是具有统计学显著意义的阳性结果，则更易或更快发表[48]。因此，为充分考虑发表偏倚对研究结果产生的上述影响，保证元分析的可靠性，我们采用漏斗图进行发表偏倚评价。 漏斗图主要以视觉观察进行发表偏倚识别，它以效应量为横坐标，纵坐标为标准误，两条斜线为95%可信区间；在理想状态下，应有95%的点落在此区间，且小样本所得的离散度较大，因此，常处于漏斗图的底部，大样本离散度较小，处于顶部；在正常情况下，应该是顶小底大，如果非上述情况，则可能存在较大偏倚。 本研究采用Rev Man 5.3 软件对纳入元分析的33 项实验与准实验研究进行发表偏倚评价， 所得漏斗图呈现结果，如图2 所示。

图2 所纳入研究的发表偏倚评价漏斗图

由图2 可知，研究大部分处于漏斗的上半部分，这意味着在33 项研究中，样本量相对较大；且研究效应量基本上在平均效应量两侧呈对称分布，可见，纳入的33 项研究的结果数据可靠性较高，可用于元分析；但有少部分点落在两条斜线外，这表示纳入的研究间可能存在异质性， 需要结合稍后得出的森林图数据进一步查看。

（五）异质性检验

由于研究间存在干预措施、样本数量、测量结果等异质性，因此，需要根据异质性检验结果，判断元分析采用的模型。异质性就是“纳入同一个元分析的所有研究间存在的差异”，异质性检验（又叫统计量的齐性检验，或一致性检验）的目的是检查各个独立研究的结果是否具有可合并性， 异质性检验方法包括统计量法与图示法。Rev Man 5.3 软件可实现的统计量法是Q 检验与I2检验， 可对二者同时查看；图示法是森林图与漏斗图。 Q 检验主要看P 值，P 值大于0.1，则无异质性，P 值小于0.1，则存在异质性。 I2反映的是异质性部分在效应量总的变异中所占的比重，由于即I2是根据Q 统计量转换得到的，因此，I2统计量较Q 统计量敏感，且I2取值范围是0-100%，取值越大，异质性越大:0-25%为无异质性，25%-50%为轻度异质性，50%-75%为中度异质性，75%以上为重度异质性，一般50%左右异质性均可接受。若各研究结果间无显著异质性差异，则采用固定效应模型；反之，需要进一步分析异质性来源， 采用亚组分析、Meta 回归或敏感性分析探索异质性来源，在排除明显异质性的影响后，再采用随机效应模型进行元分析。

由于所得漏斗图显示可能存在异质性，因此，我们采用Rev Man 5.3 软件对纳入的33 项研究绘制了固定效应模型的森林图， 以进一步进行异质性检验。所作森林图显示的结果为:异质性检验的结果是卡方值为483.97，自由度为39，P 值小于0.01，说明33 项研究间存在明显的异质性；同时，I2值为92%，进一步验证了33 项研究间的异质性显著。这与漏斗图呈现的结果相同，因此，在分析前需要进行异质性消除。 敏感性分析包括剪补法、失安全系数法、去除单项研究法以及选择模型分析法。 本研究采用的是敏感性分析中的去除单项研究法， 对存在明显差异的研究进行删除，并重新进行元分析，查看合并效应量的变化情况， 最终去掉有明显差异的8 项研究（如，Wang.et al、La Paglia.et al、Sengupta.et al、Lee、Berland.et al、Jakosˇ.et al、Basu、Jun.et al）。 同时，采用随机效应模型进一步消除异质性，由此得到图3 所示的漏斗图与表2 所示的异质性检验结果。 异质性检验的结果是卡方值为62.01， 自由度为27，P 值小于0.01，I2值为56%，与之前相比，异质性大大减少，且I2值在50%左右，分析结果可以采纳。

图3 消除异质性之后的漏斗图

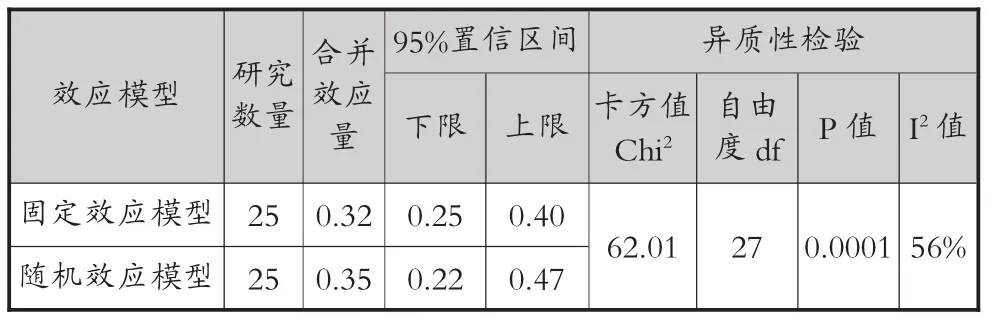
表2 消除异质性之后的异质性检验结果

四、研究结果

（一）K-12 教学促进计算思维发展的总体效果

在异质性消除之后，对所得25 项纳入文献进行作图分析，得到的“K-12 教学支持计算思维发展”的总体效果森林图，如图4 所示。 在森林图左侧，所显示的是纳入研究的具体数据， 最下方分别是统计后的合并效应量与95%置信区间、 异质性数据与合并效应量检验。在森林图右侧中，顶端的字母分别代表统计指标、统计方法、效应模型、置信区间，横线代表单项研究的可信区间，即此研究真实存在的范围。横线越长，样本量越小，结果越欠可靠；横线越短，样本量越大，结果越可靠。横线上的点代表单项研究的效应量，点的大小代表研究的权重，也就是该研究对此元分析做出的贡献度。

如图4 显示， SMD 合并效应量为0.35，95%置信区间是（0.22，0.47），最终的落脚点是在直线右侧，合并效应量检验（Test for Overall Effect）Z 值为5.52（P ＜0.001），达到显著水平。且根据Cohen 的效应统计理论，效应量在0.2 之内，轻度影响；0.2-0.8 之间，中度影响；大于或等于0.8，显著影响[49]。 “K-12 教学支持计算思维”总体效果的合并效应量（SMD=0.35）处于0.2 与0.8 之间，且落在直线右侧，为中度积极影响。 这表明，计算思维教学总体能够提升K-12 学生的计算思维水平。

图4 “K-12 教学支持计算思维”的总体效果森林图

（二）K-12 教学促进计算思维发展的具体效果

为了解K-12 教学促进计算思维发展的具体效果，我们从学业成就、思维技能、合作关系三方面，对三类作用效果进行元分析。 如表3 所示，总体合并效应量达到0.71， 处于0.2-0.8 之间， 且Z=5.51（P＜0.001），达到统计量显著水平，同时，异质性检验[Chi2=2.63，df=2 （P= 0.27），I2=24.0%] 的I2值小于50%，表明三类效应值使用情况之间无显著性差异。具体来讲，学业成就类的合并效应量大于0.8，为显著影响，表明目前研究者主要采用编程成绩、学科成绩或作品绩效等学业成就指标来评价计算思维；思维技能类与合作关系类作用效果的合并效应量均处于0.2-0.8 之间，说明二者对计算思维评价方式的影响为中度， 表明后续研究尚需要进一步关注思维技能与合作关系的评价。

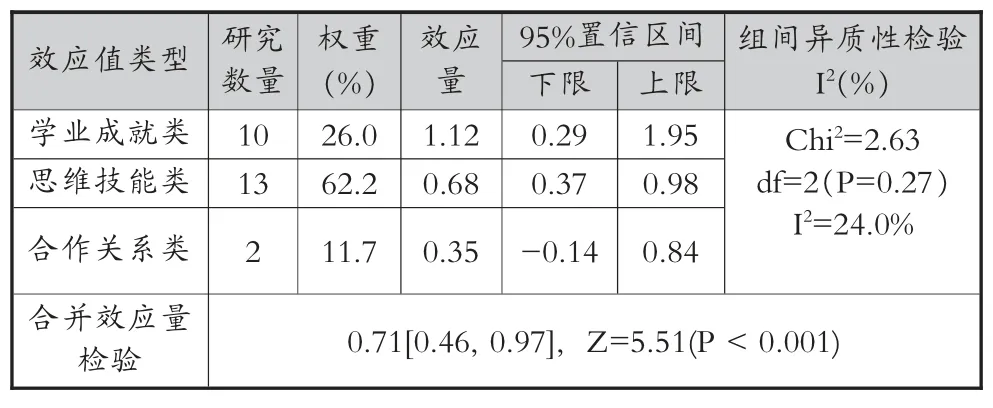
表3 K-12 教学促进计算思维发展的具体效果分析

（三）促进K-12 计算思维培养的教学方法的应用效果

根据入选文献使用教学方法的频次， 本研究主要比较了配对编程、支架式教学、基于游戏的学习、基于问题的学习与项目式学习五类教学方法的应用效果，如表4 所示。其中，总体合并效应量达到0.62，处于0.2-0.8 之间，且Z = 4.74（P＜0.001），达到统计量显著水平， 表明上述五类教学方法对计算思维培养呈中度积极影响作用。 同时， 异质性检验[Chi2=2.35，df=4（P=0.67），I2=0%]的I2值小于50%，表明上述五类教学方法之间没有显著性差异。具体来讲，项目式学习与配对编程的合并效应量分别为1.79、0.95，均大于0.8，为显著影响，即采用项目式学习、配对编程教学方法可有效促进学生计算思维的提高；其次，支架式教学、基于游戏的学习、基于问题的学习的合并效应量均处于0.2-0.8 之间，为中度积极影响。

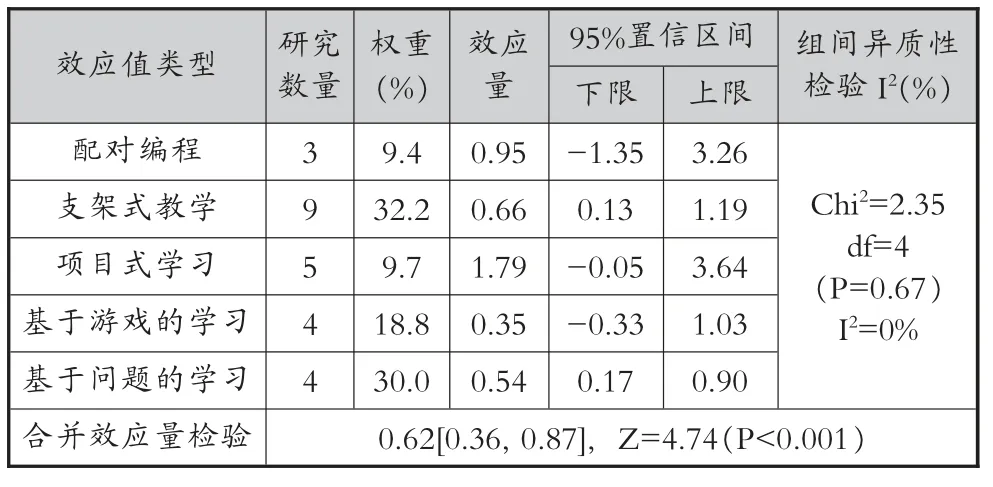
表4 不同教学方法对计算思维培养的应用效果分析

（四）K-12 计算思维发展的研究设计效果

将K-12 计算思维发展的研究设计从研究样本量、研究学段、研究时长、研究学科四个方面进行分析，所得详细数据结果，如表5 所示。 研究结果如下:（1） 四个方面的总体合并效应量均为0.71，Z=5.15（P＜0.001），处于0.2-0.8 之间，达到统计量显著水平，表明研究设计的四个方面能够显著影响计算思维的发展；（2）实验学科的组间异质性有差异（I2=90.1%），且跨学科课程的合并效应量为2.67，远大于0.8，因此，跨学科的整合设计对计算思维培养效果具有重要影响；（3）研究样本量、研究学段、研究学科的组间异质性均无显著差异 （I2均小于50%），相对而言， 研究样本量为200 人以上 （效应量为1.89）、研究时长在2 周以内（效应量为1.23）对计算思维发展影响显著。

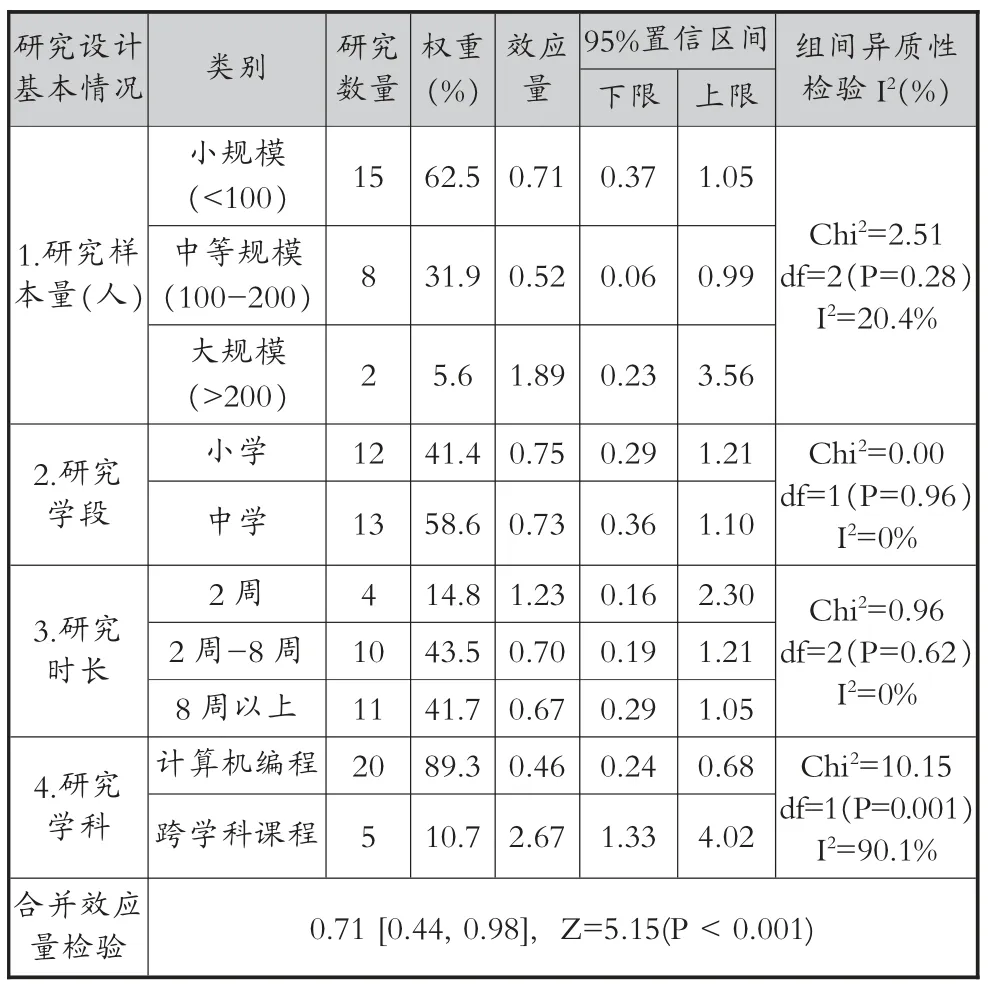
表5 所纳入研究的研究设计基本情况

五、结论与展望

我们对近13年来国际有关计算思维发展的33项高水平研究成果，进行了整体性的梳理和分析，并且依据元分析结果对计算思维教学的作用效果，进行了客观分析和评价， 分别从K-12 计算思维教学的作用效果、 不同教学方法对计算思维促进作用的差异， 以及研究设计要素对计算思维发展的影响等视角进行了分析与讨论，得到的主要研究结论如下:

（1）K-12 计算思维教学总体对计算思维发展具备正向的促进作用， 但对思维技能与合作关系发展的作用效果尚待进一步关注。元分析结果显示，计算思维教学对于学业成就类具有高水平的作用效果，而对思维技能类与合作关系类的促进作用则为中等水平。这意味着目前计算思维教学的作用效果，主要体现在学业成就上，包括项目绩效、编程成绩、学科成绩等[50]；而对思维技能与合作关系两类的作用效果有待进一步提升。从计算思维的本质来看，计算思维需要培养学生的问题解决思维能力， 需要发展学生的问题解决思维、批判性思维、算法思维、反思性思维以及创造力等抽象思维。 这些思维能力的提升是一个相对漫长复杂的过程， 需要后续大量研究与实践进一步追踪监测。 值得注意的是，在计算思维发展研究中，还较少有研究关注到合作关系。 大多数研究只将小组合作作为教学方法，并未将其作为衡量计算思维作用效果的一部分。 例如，Brennan 与Resnick提出的计算思维三维理论框架，就是从合作关系角度定义计算思维发展水平[51]，后续还需要大量的相关研究来关注计算思维培养中的合作关系发展。

此外， 关于思维技能与合作关系的评价工具与方法还有待进一步加强。从评价工具来看，研究者主要是根据自己的研究需要自行开发量表， 尚缺少分析思维技能与合作关系的统一标准化评价工具，由于量表质量参差不齐， 可能导致评价结果缺乏可比性；从评价方法来看，有学者开始探索采用操作行为记录[52]、半结构化反思日志等方式，收集思维技能与合作关系发展的过程性数据[53]。 如何将过程性数据与结果数据进行整合， 综合评价思维技能与合作关系，仍是后续研究需要关注的重要问题[54-55]。

（2）项目式学习与配对编程是发展计算思维的重要教学方法。元分析结果显示，项目式学习、配对编程的应用效果最为显著；支架式教学、基于游戏的学习、基于问题的学习三类教学方法， 为中度显著性影响。项目式学习可以设计跨学科的复杂任务， 以引导学生综合运用学科知识与计算思维技能形成项目成果，可能有助于综合发展计算思维[56]。如，Kim 设计了长达16 周的创造性培训项目，学生通过Scratch 创建交互式故事，提高了学习兴趣、编程知识与问题解决能力[57]。

配对编程则是一种协作教学法， 通过设定代码编写者与核查者两种协作角色分工， 依靠双人使用一台计算机来协作完成编程任务。 与其他协作教学法相比，配对编程的优势在于任务与角色划分明确，致使协作的效率较高， 两位参与者可以各自发挥自己的知识与技能优势，进行有效协作[58-59]。 如，Denner 与Zhong 的实验研究结果均表明， 与单独编程相比，配对编程（PP）是培养学生计算思维的有效方法，具有明显优势。同伴使用电脑的经验和协作态度会影响其协作伙伴，有利于培养积极的、有信心的编程意识与合作意识[60-61]。

（3）跨学科综合研究设计对于发展K-12 学生的计算思维具有重要的价值。 元分析结果显示，跨学科的整合设计对计算思维培养效果具有重要影响。图灵奖获得者Karp 教授也指出， 跨学科综合设计能够帮助学生迁移问题解决方案，使学生能够逐步理解问题并生成问题解决路径[62]。 具体来讲，计算思维的发展需要学生运用计算机等工具，进行抽象表征以寻求问题解决最优化方案。 在寻求问题解决方案的过程中，学生需要对成熟的问题解决思路或方案进行迁移，以解决新情境下的问题。 因此，迁移对于计算思维的培养具有重要价值。而跨学科课程设计能够帮助学生对不同情境下问题解决方案进行抽象、重组，从而迁移问题解决思路。 同时，跨学科还有助于计算思维在不同知识领域进行迁移[63]。 如，Ioannidou 等人试图研究如何将游戏中获得的计算思维转移到数学课程中[64]；Repenning 等人探索了如何将计算思维从游戏迁移到科学问题模拟中[65]。 因此，跨学科综合设计能够促进问题解决思路及计算思维在不同学科中进行迁移，从而增强计算思维培养的效果。

后续研究可从以下几方面进一步加强:

第一，关注计算思维发展的整合教学法，构建创新融合的教学方法体系。 从计算思维的内涵来看，计算思维发展需要针对复合的目标体系， 现有单一教学法的应用，存在一定的局限性。 为此，研究者与实践者需要整合相互补充的教学法， 以形成教学方法体系。 如，针对配对编程中存在的“依赖同伴、消极参与”现象，可通过整合同伴互评以及支架式教学等教学方法予以解决[66-68]。 因此，从计算思维发展的复合目标体系出发，选取并整合多重教学法，是后续实证研究应关注的重点。

第二，以跨学科课程为设计重点，促进计算思维在不同学科中进行迁移。 周以真教授指出，计算思维是关于任一学科的探究过程， 而不仅仅局限于计算机科学[69]。 美国采用的下一代科学标准（Next Generation Science Standards-NGSS）提出从以下三个维度进行K-12 科学教育:科学与工程实践、跨学科核心理念以及类似科学家工作的探究理念。 将计算思维与科学教育进行融合是后续教学实践的重点[70]。英国已将计算思维纳入语言、数学、科学等学科中，为其他国家跨学科计算思维发展开辟了新的出路[71]。而我国目前主要还基于信息技术课程发展计算思维能力，因此，有学者提倡，应在其他学科教学中进一步发展计算思维能力[72]。 如何开发跨学科课程来发展计算思维， 如何促进计算思维在不同学科中进行迁移，都有待后续研究与实践。

第三，以人工智能教育应用为契机，探索计算思维发展的有效路径。 人工智能课程需要借助数学、计算机科学、物理学、生物学、心理学等多学科知识，为培养学生逻辑思维、科学思维、计算思维等高阶思维提供肥沃土壤[73]。后续研究可以借助人工智能课程的实施，进一步推动计算思维的研究与实践发展。