一道三角高考填空题的解法赏析
2019-10-14福建省三明市将乐县水南中学365300罗继淼
中学数学研究(江西) 2019年9期
福建省三明市将乐县水南中学 (365300) 罗继淼
一、原题呈现
(2018年江苏卷第13题)在ΔABC中,角A,B,C的对边分别为a,b,c,∠ABC=120°,∠ABC的平分线交AC于点D,且BD=1,则4a+c的最小值为.
二、试题解析
分析:首先寻求a和c的关系,再运用均值不等式或判别式法求解.
解法1(等面积法):如图1,∵SΔABC=SΔABD+SΔBCD,
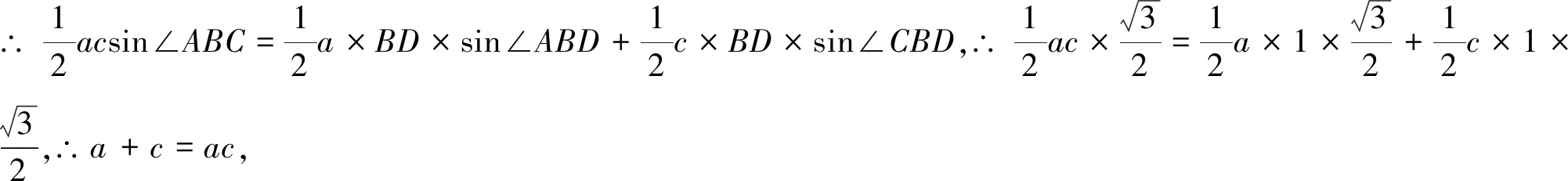
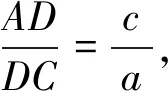
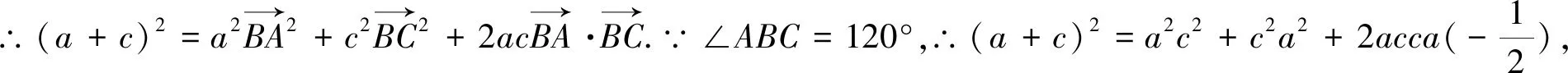
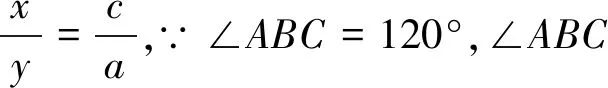
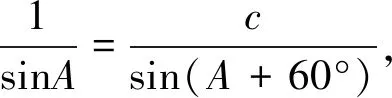
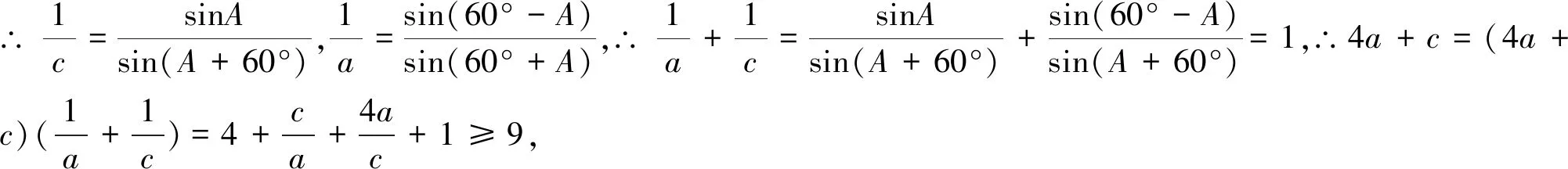
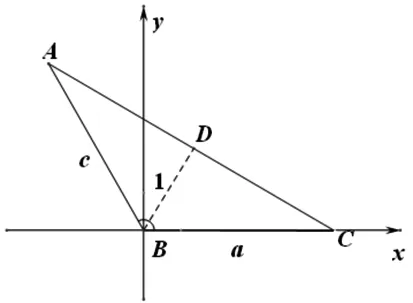
图2
解法5(坐标法):如图2,以B为原点,BC所在直线为x轴建立平面直角坐标系xoy.易求B(0,0),C(a,0),
又A,D,C三点共线,故kAC=kDC.又kAC=
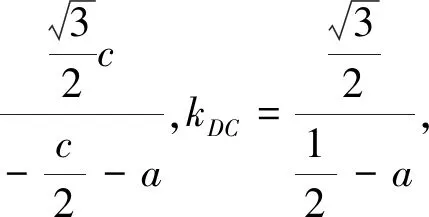
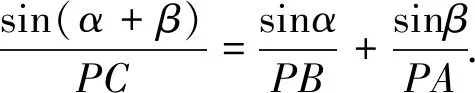
证明:如图3,如果三点共线,那么SΔPAB=SΔPAC
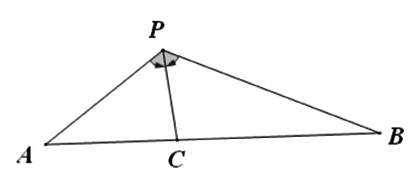
图3

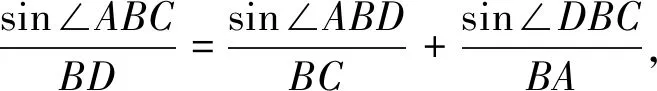
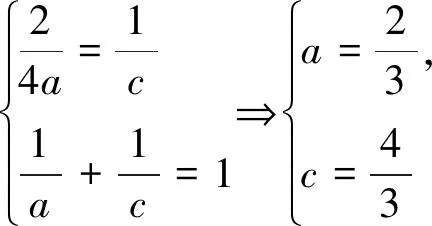
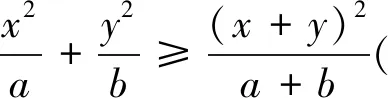
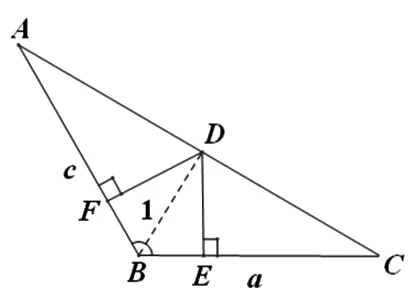
图4
解法7(几何法):

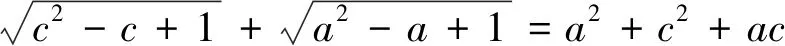
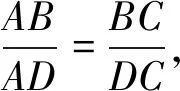
后续解法:此题若能求出a和c的关系式a+c=ac,则接下来求4a+c的最大值也是有多种方法进行求解的.即有如下解法:
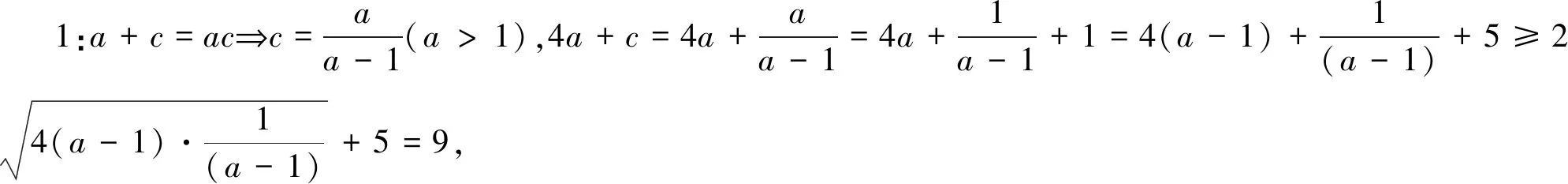
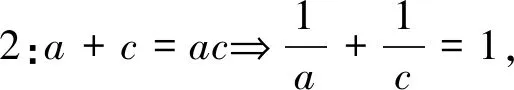

解法3:a+c=ac⟹(a-1)(c-1)=1,则
4a+c=4(a-1)+(c-1)+5≥

