靶机拖带诱饵飞行对性能影响分析

李红泉

(中国人民解放军92419部队,辽宁兴城 125106)

经历了数十年的发展,无人机技术已经相当成熟,广泛应用于社会诸多领域,成为表现最活跃的航空产品之一[1],特别是执行超越生理极限的机动飞行或恶劣气象、生化采样等极危险任务,具有独特优势[2]。军事方面,由于在中东战争中的出色表现,各国军队纷纷发展攻击型无人机,使其担负大量的作战任务[3],但平时,无人机更多用在部队军事训练上,或用于验证各种防空武器的技术性能,于是催生了无人机的一个重要分支——靶标的进步。靶标是一种动态实物航空模拟器,是防空武器所要攻击目标的替代物,用于防空武器的研制性试验、鉴定、效能评估,以及部队训练和演习[4]。鉴于现在作战飞机已经发展到第四代,为检验第四代战斗机作战性能,满足空战训练,为防空部队防御第四代战斗机的导弹提供目标,应开展研制相应性能的靶机[5]。

一款先进的靶机不一定都是新研产品,受研制经费、研制周期、可靠性的限制,推出新型号的过程相当漫长,且还要担负失败的风险,因此,各国普遍在成熟产品上进行升级改造衍生出新型号的方法,比如美国的石鸡/火蜂靶机,先后服役几十年、十多个型号、近十万架,陪侍了几代航空武器。本文提及的导弹形的流线体拖曳诱饵的主要结构参数,以具有一定尺寸和挂装能力的大型涡喷靶机作为研究对象,采取飞行器设计的通用方法[6-8],进行靶机挂载拖曳诱饵性能分析,计算释放诱饵之后靶机参数变化,开展使用靶机模拟作战飞机实施拖曳诱饵[9]干扰的预先研究,为靶机功能升级做前期论证工作。

1 计算内容与基本假设

挂载、释放并拖带诱饵飞行,势必造成靶机性能的变化,主要计算五个方面的影响。

1)释放诱饵后,靶机的速度变化;

2)释放诱饵后,需要多大的升降舵偏角,可使靶机继续水平飞行;

3)释放诱饵后,靶机的迎角变化;

4)释放诱饵后,需要多大的方向舵偏角,可使靶机继续沿航向飞行;

5)释放诱饵后,靶机的偏航角变化。

为降低计算复杂程度,设计靶机的两端翼尖均加装拖曳诱饵(或外型配平),保持整体对称布局。飞行过程忽略了部分扰动的影响,并作合理假设,分别是:

1)靶机在释放诱饵之前保持稳定的平直匀速飞行状态;

2)释放过程缓慢稳定,忽略释放造成的动态响应;

3)释放过程及释放之后无突风;

4)假设释放诱饵后发动机推力无变化;

5)缆绳呈直线状态,质量不变;

6)忽略飞机自动增稳系统的作用。

计算中建立地面坐标轴系、机体坐标轴系、气流坐标轴系及稳定性坐标轴系,坐标系遵循右手定则和转换方法,迎角、侧滑角由机体坐标轴系定义,拖曳体阻力系数、摩擦系数、静导数等经验值取自参考文献[10]中导弹类飞行器的图表数据。

2 计算方法

2.1 模型参数及符号定义

计算所需靶机的主要模型参数有:机翼面积、翼展、气动弦长、起飞重量、推重比、升阻比、纵向及航向操纵导数等;拖曳诱饵的主要模型参数有:直径、长度、缆长、缆径、诱饵重量、升阻比、表面摩擦系数等。使用的符号定义见表1,靶机拖带诱饵飞行示意见图1。

表1 符号定义

图1 靶机拖带诱饵飞行示意

2.2 速度变化

从靶机升阻比求出释放诱饵后系统的阻力系数,根据阻力计算公式求出稳定拖带的飞行速度。

由阻力公式和升阻平衡关系,靶机阻力

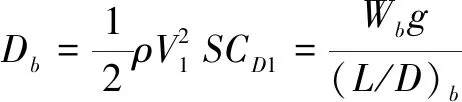
(1)

式中,CD1为释放诱饵后系统总的阻力系数,包括四部分,即

CD1=CDtow+CDline-fri+CDline-pre+CDb

(2)

式中,CDtow为诱饵阻力系数;CDline-fri为缆绳的摩擦阻力系数;CDline-pre为缆绳的压差阻力系数;CDb为靶机阻力系数。

根据导弹类飞行器数据选取诱饵升阻比,则

(3)

(4)

式中,Cfe为等效表面摩擦系数,Set为缆绳外露面积。

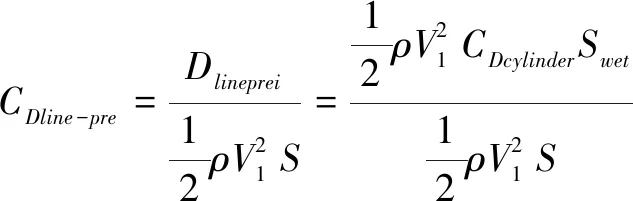
(5)

式中,CDcylinder为圆柱体在该雷诺数下的阻力系数。

(6)

再由式(1)、(2),计算出释放诱饵后速度。

2.3 配平所需升降舵偏角

将诱饵和缆绳作为一个整体进行受力分析,诱饵和缆绳的重力和阻力合并计算,已知诱饵和缆绳阻力之和为

缆绳与水平面间夹角

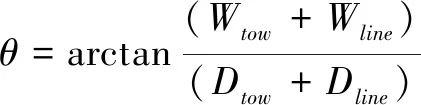
(7)

缆绳拉力

(8)

根据缆绳与靶机的作用点距离靶机重心之间的纵向距离DX,计算俯仰力矩

Mm=F×sinθ×DX

(9)

由俯仰力矩系数

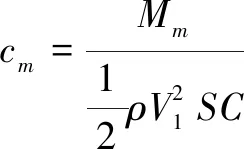
(10)

最后求得升降舵舵偏

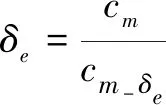
(11)

2.4 迎角的变化

迎角

(12)

计算的数值结果表示释放诱饵后,如果不改变舵偏,靶机迎角增加情况。

2.5 配平所需方向舵舵偏

根据翼展长度和机身直径,计算缆绳作用点距离靶机重心之间的横向距离DY。

偏航力矩

Mn=F×DY

(13)

偏航力矩系数

(14)

方向舵舵偏

(15)

根据计算结果,可知靶机沿原航向飞行需要施加的方向舵舵偏量。

2.6 靶机侧滑角的变化

侧滑角

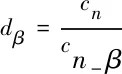
(16)

结果表示释放诱饵后,靶机将向左偏航(释放左翼诱饵)角度。

3 算例分析

输入拟拖带诱饵飞行的靶机主要模型参数和设计的诱饵系统主要模型参数,按照前述方法可计算出靶机翼尖拖带诱饵对其性能影响结果,对比防空武器的靶标要求,论证靶机模拟作战飞机实施拖曳诱饵干扰的情况。

根据飞机典型飞行环境,选取靶机在H=8 000 m、V=250 m/s,H=8 000 m,V=200 m/s,H=10 000 m、V=250 m/s,即相同高度、不同速度和相同速度、不同高度三种工况下靶机拖带诱饵飞行的状态变化。计算结果见表2。

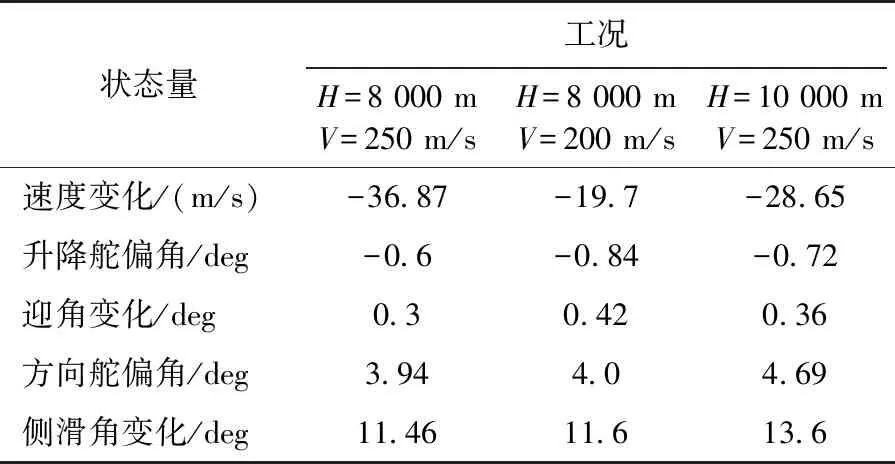
表2 不同工况的性能比较

分析表2中数据可知:

1)随着飞行高度的降低,飞行速度变化量明显增大,而靶机姿态所受的影响变化不大,因此应在高空高速飞行;

2)随着靶机飞行速度的降低,飞行速度变化量明显减小,靶机姿态所受的影响变化不大,呈微增趋势;

3)速度、航向姿态和方向舵偏角的变化较大,主要是由拖曳系统的阻力引起,而缆绳阻力在所有增加的阻力中占的比重最大,这是由于缆绳的外形造成后方流动分离现象严重,压差阻力较大;

4)俯仰姿态和升降舵偏角的变化较小,主要是因为缆绳与靶机的连接点距离重心的纵向距离近,俯仰力矩较小。

4 结束语

与理论计算相比,科研人员还普遍使用专业软件进行飞行器设计工作,但软件需要建立三维模型并有限元划分,对从业者的专业水平和数据处理设备要求较高。对于成熟飞行器的设计改造,利用已有的模型参数,使用本文介绍的计算方法,可以快速得出结果数据;若使用Matlab等运算软件,仅修改个别参数就可以进行批处理计算,较为便捷,适合于设计的最初阶段。

靶机在基本型上衍生改造,也是一种迭代调整优化过程。研究大型靶机模拟拖曳干扰的可行性,需保持系统可靠性,定型的靶机不宜在外形结构上进行大的改变;主要考虑靶机最大载荷条件下,允许的飞行包线,在可接受范围内,逐步增大拖带诱饵的尺寸,从而增加干扰功率和欺骗性能,往复计算中找到最优设计方案。另外,文中介绍的计算方法均有通用性,对其他飞行器的设计改进工作或可提供某些参考。