一种以测量关键特征拟合舱段位姿的方法

2019-10-12李世其王峻峰

中国机械工程 2019年18期

陈栋李世其王峻峰丰意何旺

华中科技大学机械科学与工程学院，武汉，430074

0 引言

总装对接是确保航空航天类产品成功制造的关键环节。实现总装对接的数字化装配系统主要由测量系统、控制系统、对接执行机构和数据处理软件等组成。测量系统通常采用激光跟踪仪和iGPS等数字化设备采集目标部件的空间位姿数据并反馈到数据处理软件中，进而引导对接执行机构实现部件总装对接[1-2]。其中，总装部件的位姿测量是确保对接任务顺利实施的前提和关键，通过研究空间位姿测量及拟合方法对于提高位姿测量精度并确保装配准确度具有重要意义和价值。

目前，刚体位姿测量及解算一般通过测量刚体上的多个位姿基准点并作为换算点，从而将刚体位姿求解问题转换为参考坐标系和刚体连体坐标系之间的点集匹配问题，然后再通过点集匹配算法进行求解[3]。例如，文献[4]研究并比较了奇异值分解法、三点法和最小二乘法计算飞机大部件位姿及精度问题。文献[5]提出了一种基于单目视觉四元数法的解析方法解决航天器相对位置测量和姿态参数估计的问题。文献[6]将机翼姿态评估问题转化为空间点与曲面之间的配准问题，提出了一种基于ICP(iterative closest point)算法的姿态评估方法。此外，文献[7]还提出了一种矢量位姿求解法，通过在圆柱体舱段上按照一定规则布置测量特征点以求解得到舱段位姿参数。该方法对特征点的布置技术要求较高，实现较为困难。虽然以上基于点集匹配的方法在拟合刚体位姿时能够得到较为满意的效果，但需要事先在刚体上加工多个精度较高的位姿基准点以满足测量需求，这对于某些难以更改产品设计和加工工艺的航天产品并不实用。针对这类无法设置标记点的刚体位姿测量问题，目前研究较多的是通过测量关键特征的方法获取刚体位姿。文献[8]提出了一种基于关键装配特性的最佳装配位姿拟合方法，以装配关键特性相关公差的重要程度构建了最小综合偏差函数，进而获取装配体间的最佳装配位姿。文献[9]针对飞机部件的位姿测量问题，提出了利用外型面关键特征来构建部件的对接向量，最后进行位姿拟合的方法。文献[10]提出了一种测量辅助装配方法框架以实现基于关键测量特性的过程集成和数据融合。本文与以上基于测量关键特性的位姿求解方法的不同之处在于，本文先在待测量部件上选取加工精度较高的直接关键特征，经激光跟踪仪采点测量后，利用改进的最小二乘法剔除直接关键特征中的粗差测量点，再用其余合格测点拟合得到多个间接关键特征。最后通过融合间接关键特征构建出待测部件的坐标系，并获得相应的位姿参数。本文以圆筒形舱段为例，在仿真试验中利用所提出的方法求得了满足对接任务需要且精度较高的舱段位姿参数。

1 空间位姿的表达方法

在图1所示的总装对接场景中，以激光跟踪仪所在的测量坐标系为全局坐标系，则部件的空间位姿可用部件连体坐标系相对于测量坐标系的变换关系来表示。

一般情况下，可将部件位姿按向量方式表示为(x,y,z,α,β,γ)T。其中，(x,y,z)T为部件坐标系原点在测量坐标系中的位置分量，(α,β,γ)T为部件坐标系相对于测量坐标系的姿态角。

(1)

式中，sα表示sinα，cα表示cosα，依此类推。

2 关键特征提取及连体坐标系构建

由于在待测部件上无法事先加工测量基准点，本文采用了测量关键特征的方式间接构造部件坐标系以获取其位姿参数。下面以图2所示的固定段为例，通过关键特征来构造其连体坐标系。

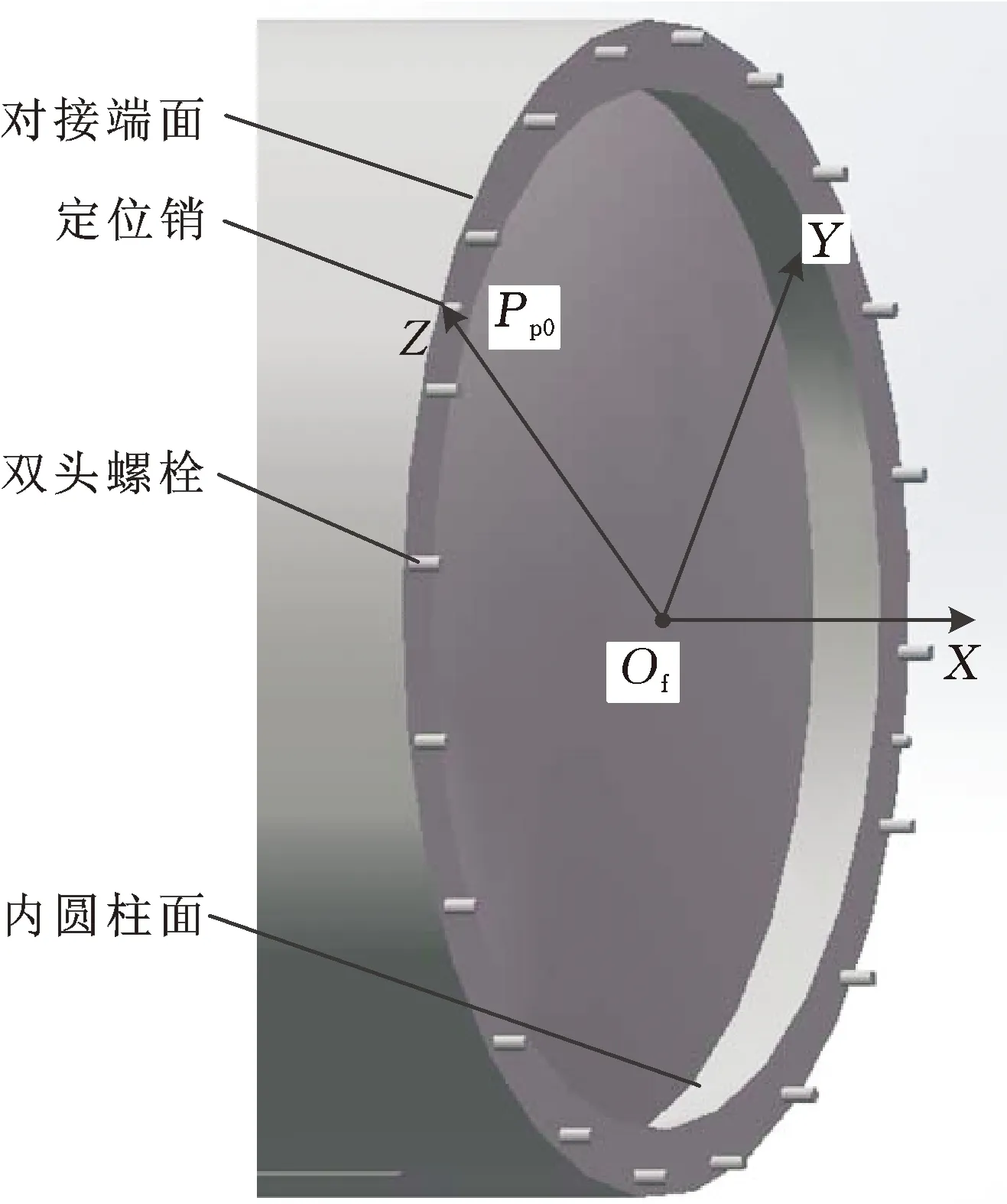
图2 舱段坐标系构造示意图Fig.2 Schematic diagram of cabin coordinate system

根据固定段外型面及连接螺栓加工精度较低，对接端面、内圆柱面和定位销的加工精度较高的特点，以及移动段与固定段中心轴线需具有较高同轴度的任务需求，首先选取固定段上加工精度较高的对接端面、内圆柱面以及定位销外圆柱面作为直接关键特征，经激光跟踪仪采点测量并拟合。然后通过拟合直接关键特征构造出舱段中心轴线、对接端面法线及定位销轴线等间接关键特征。最后融合间接关键特征构造出舱段的连体坐标系：具体是沿对接端面的法矢量方向建立X轴，以对接端面与内圆柱面轴线的交点构造坐标系原点Of。若记对接端面与定位销中心轴线的交点为Pp0，则沿原点Of与Pp0连线的矢量方向建立Z轴，最后Y轴由右手定则确定，从而构造固定舱段连体坐标系F，即OfXYZ。

3 关键特征拟合及位姿参数求解

若根据图3所示的逻辑结构图构造坐标系F，则需要先拟合出内圆柱面及定位销的空间中心轴线，再求取相应交点。本文采用一种先将测量点投影再拟合投影点的方法直接求取空间中心轴线与对接端面的交点，避免了复杂的空间直线拟合。因此，坐标系F的构造包括对接端面的拟合以及空间中心轴线与对接端面交点的拟合。

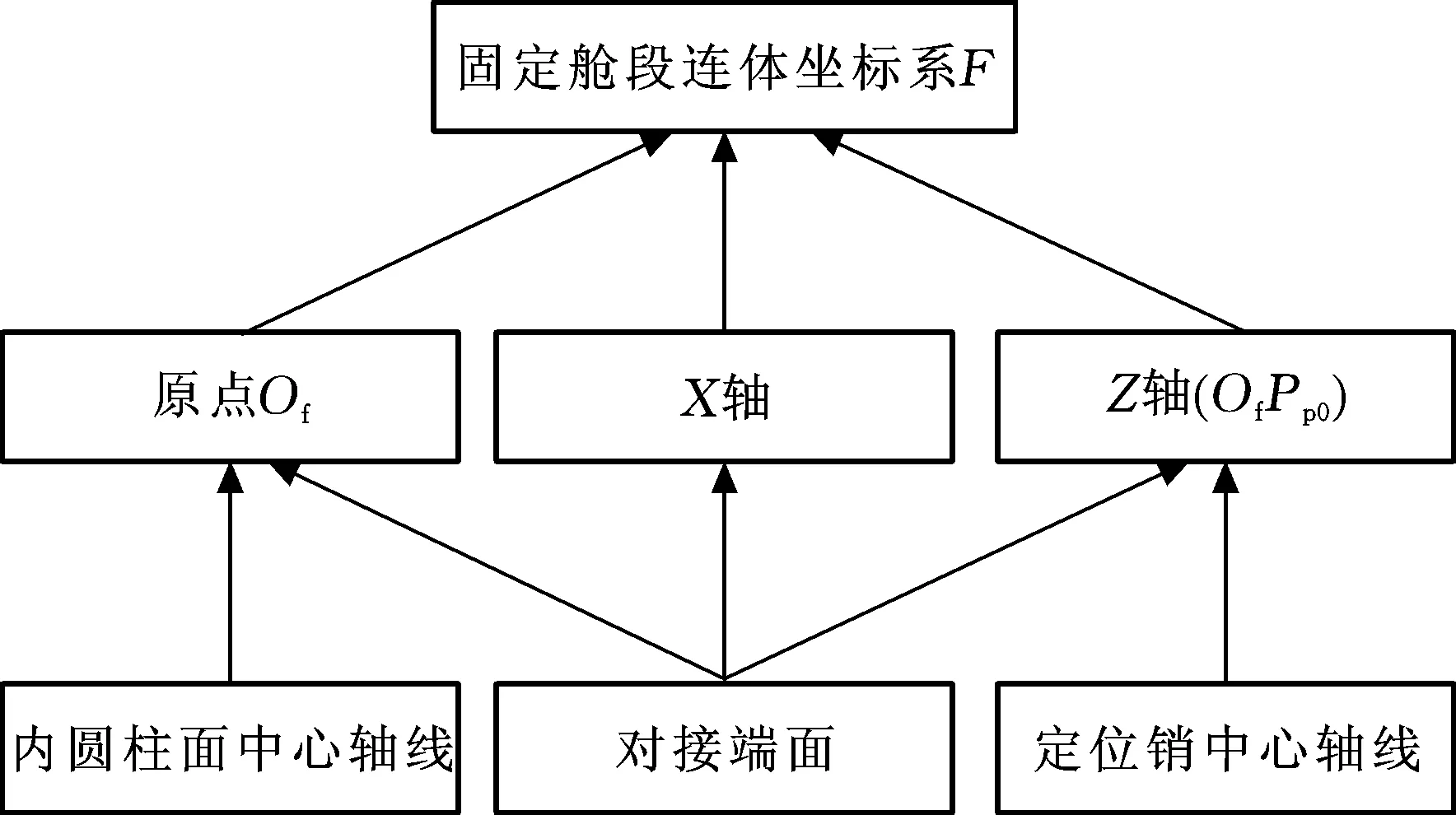
图3 固定舱段连体坐标系构造结构图Fig.3 Construction diagram of cabin coordinate system

3.1 对接端面的拟合

在舱段对接端面上选取n个点，坐标系在L下测得坐标为P1i=(x1i,y1i,z1i)T，i=1,2,…,n。由于实际中对接端面不经过坐标系L的原点，因此对接端面P的方程可表示为

Apx+Bpy+Cpz+1=0

(2)

其中，Ap、Bp、Cp为该平面方程系数。

将以上n个测点坐标代入式(2)并由最小二乘法拟合得到系数向量：

(3)

以Sn=(Ap,Bp,Cp)T表示对接端面法向矢量，可沿其单位向量u=Sn/|Sn|方向构建坐标系F的X轴。

3.2 空间中心轴线与对接端面交点的拟合

本文以内圆柱面中心轴线与对接端面交点Of的拟合为例，介绍空间直线与平面交点的拟合方法。首先从固定段的内圆柱面上选取m个点测量，以拟合的对接端面为基准投影面，得到m个投影点。然后，利用投影点拟合出空间圆。该空间圆可看作球面与平面的截交线，圆心可看作球心在平面上的投影点，即为坐标系F的原点Of。

在内圆柱面上利用激光跟踪仪选取m个点P2i=(x2i,y2i,z2i)T(i=1,2,…,m)测量，以对接端面为投影基准面，根据投影点与对接端面互相垂直的约束条件，可解得m个投影点P3i=(x3i,y3i,z3i)T的坐标分量为

(4)

设空间球面S的方程为

Asx+Bsy+Csz-Ds=x2+y2+z2

(5)

式中，As、Bs、Cs、Ds为球面方程系数。

将所求投影点P3i代入空间球面方程，并根据最小二乘法拟合球面系数向量：

(6)

解得球心坐标Pc=(As/2,Bs/2,Cs/2)T。

将Pc投影于对接端面得到原点Of，按照式(4)即可求得Of坐标(xf,yf,zf)T。

此外，在定位销上选取k个测量点，同理可拟合出定位销轴线与对接端面的交点Pp0，并得到舱段坐标系F的Z轴单位方向向量。再结合所拟合X轴和原点Of，即可构造出坐标系F。

3.3 舱段位姿参数求解

由坐标系F各轴单位矢量与旋转矩阵R的关系得

(7)

其中R第一、二、三列分别为坐标系F的X、Y、Z轴单位矢量在坐标系L下的表达。联立式(1)与式(7)求得姿态角：

(8)

坐标系F原点Of向量表示在坐标系L下的平移矢量T：

T=(xf,yf,zf)T

(9)

4 基于2σ准则的最小二乘法改进

根据测量平差理论，在利用激光跟踪仪进行位姿测量时，主要存在随机误差、系统误差和粗大误差这三种误差[11]。其中粗大误差主要是由于对仪器操作不当或地基震动引起的，受其影响的测量点称为粗差异常点。当利用传统最小二乘法进行拟合时，粗差异常点会使其拟合结果偏离真实值，尤其是当数据量较少且粗差较大时，拟合结果会存在较大误差，产生严重失真。所以粗大误差对基于传统最小二乘法的位姿计算方法的拟合结果影响较大，即容错性较差[12]。

在对接端面和中心轴线与对接端面交点的拟合过程中，均用到了传统的最小二乘法，对其改进的基本思路是：利用2σ准则对最小二乘法的数据源进行探测筛选以识别其中的粗差异常点，即将残差分布在±2σ范围外的测点视为粗差异常点，通过对剔除粗差异常点后的测点进行最小二乘拟合以得到精度更高的拟合结果，从而获得更准确的位姿参数。

4.1 基于改进最小二乘法的对接端面参数求解

(1)计算n个测点P1i到对接端面的距离：

(10)

(2)计算n个距离Di的算术平均值：

(11)

(3)计算残差Ui：

(12)

(4)计算标准差σ1：

(13)

(5)精度判定：若|Ui|≤2σ1，则保留该测点；否则作为粗差点剔除。

(6)利用保留的测点由最小二乘法拟合出新的对接端面方程，按照以上步骤迭代计算，直到获得最佳的平面方程系数。

4.2 基于改进最小二乘法的原点坐标求解

(1)计算m个投影点P3i与原点Of的距离：

(14)

(2)计算m个距离Dio的算术平均值：

(15)

(3)计算残差Uio：

(16)

(4)计算标准差σ2：

(17)

(5)精度判定：若|Uio|≤2σ2，则保留该测点；否则作为粗差点剔除。

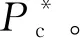
5 数值仿真试验

舱段位姿测量试验现场如图4所示。根据三维模型与现场实物的坐标匹配关系，固定舱段坐标系F相对于测量坐标系L的理论位姿为(-101，197.689，-2 592.893，-31.448°，0，0)T。

图4 固定舱段位姿的测量现场Fig.4 Scene of pose measurement of fixed cabin

利用FARO vantage激光跟踪仪作为测量设备，在现场通过手持靶球的方式在固定舱段的三类关键特征上即舱段对接端面、内圆柱面及定位销表面采点测量用于特征拟合及舱段位姿坐标系构建。测点在坐标系L下的坐标由CAM2 Measure软件采集，如图5所示,分别记录于表1、表2和表3。表中的序号表示了前文中在各特征上选取的测点个数，即n=m=k=12。

图5 固定舱段位姿测点数据采集Fig.5 Data collection of pose measurement of fixed cabin

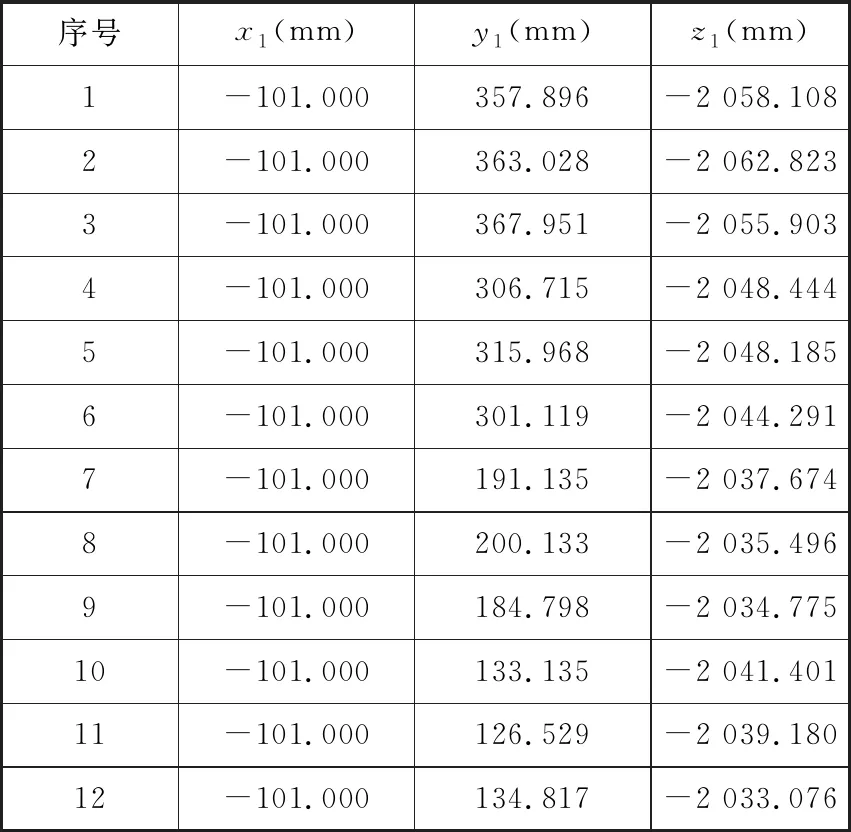
表1 对接端面测量点坐标Tab.1 Coordinates of measuring points of end plane

表2 内侧圆柱面测量点坐标Tab.2 Coordinates of measuring points of internal cylinder

根据表1～表3的测点数据，利用本文提出的以关键特征拟合舱段位姿的方法，首先结合最小二乘法对舱段位姿进行求解。然后通过对比2σ准则改进测点数据误差前后与最小二乘法求解结果在精度上的差异，验证基于2σ准则改进最小二乘法求解位姿的有效性和实用性。

表3 定位销销轴测量点坐标Tab.3 Coordinates of measuring points of dowel pin

首先在所有测量点坐标中引入幅值分别为0，0.004 mm，0.008 mm，0.012 mm，0.016 mm，0.020 mm的随机误差，此外，在所有测量点中，将1.000 mm误差随机赋予其中一点作为粗差异常点。用来验证基于2σ准则的改进最小二乘法在不同随机误差和粗大误差下，求解舱段位姿的精度及求解精度的鲁棒性。然后对每种随机误差下的测量点利用改进前后的最小二乘法分别进行500次迭代计算，并将求得的位姿均值作为舱段位姿。表4列出了利用改进前算法计算得到的舱段位姿参数(xf1,yf1,zf1,αf1,βf1,γf1)T，表5为改进后算法计算的舱段位姿参数(xf2,yf2,zf2,αf2,βf2,γf2)T。其中，表中序号1～6分别表示从随机误差幅值由0～0.020 mm不断增加的6种情况所对应的固定段位姿参数。

表4 算法改进前位姿参数求解结果Tab.4 Results of pose parameters of traditional LSM

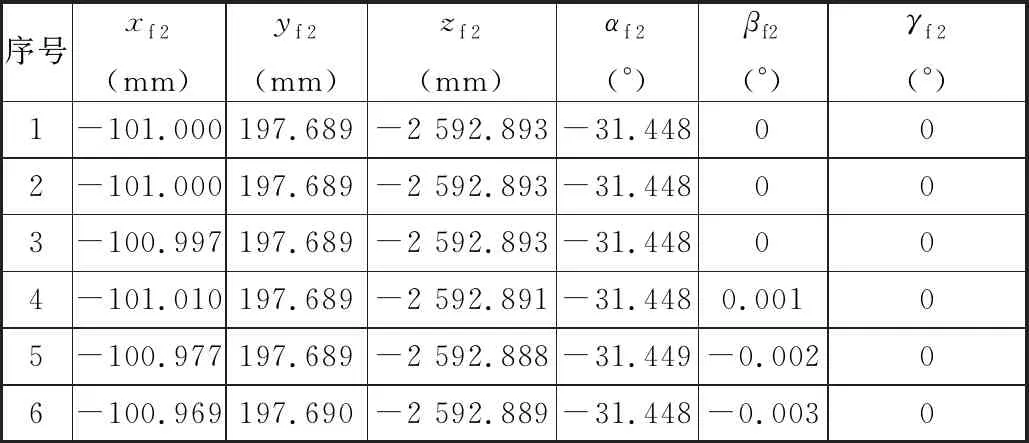
表5 算法改进后位姿参数求解结果Tab.5 Results of pose parameters of improved LSM

舱段位姿求解算法在改进前后，所求得的舱段位姿参数的绝对误差随测量点随机误差变化的关系曲线分别如图6、图7所示。

图6 算法改进前舱段位姿参数求解误差Fig.6 Errors of pose parameters of traditional LSM

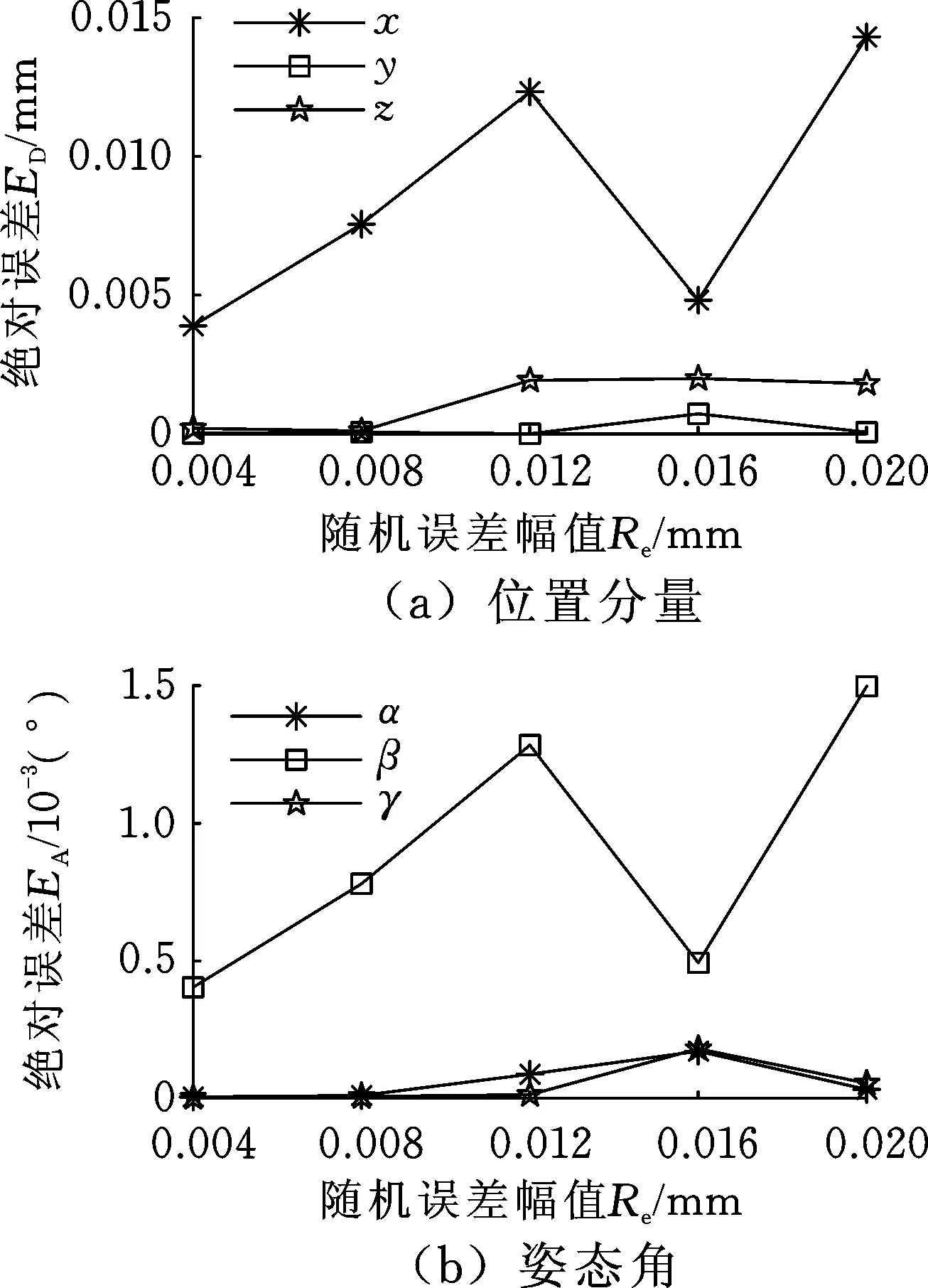
图7 算法改进后舱段位姿参数求解误差Fig.7 Errors of pose parameters of improved LSM

表4和表5的序号1中所计算的舱段理论位姿参数是在随机误差为0的情况下，分别由改进前后的最小二乘法得到。该组结果表明，改进前的最小二乘法在求解位姿参数时，所得结果的绝对误差值较大。利用2σ准则改进后的最小二乘法拟合关键特征所求得舱段位姿参数则更加接近事先给定的位姿理论值。表4和表5中，序号2～6的舱段位姿参数表明，随机误差幅值增大会影响舱段位姿参数拟合结果的绝对误差。而图6和图7中的曲线更加清楚地反映出位姿参数求解误差与随机误差的关系。图6、图7中的仿真曲线表明：改进前后的位姿拟合算法均在随机误差幅值增加的情况下，对固定舱段位姿参数拟合的绝对误差呈现出增大的趋势。对比图6和图7发现，随着随机误差幅值从0到0.02 mm不断增大，改进前后最小二乘法求解所得位姿参数的误差总体上均呈增大的趋势，但改进后的求解误差的量级明显降低。例如，在位姿分量X方向上出现的最大绝对误差值约为2 mm。而改进后的算法所求得的X方向位姿分量最大绝对误差值约为0.015 mm。可见，改进后的拟合算法在求得位姿分量时，其求解精度与前者相比降低约两个数量级。仿真结果也表明在随机误差较大时，改进前的最小二乘法求解精度较低，且随机误差增大时，对其求解精度影响较大。改进后的最小二乘位姿拟合方法更加有效，其求解精度较高，求解精度受随机误差的影响也较小。