大型航天器无控再入气动稳定性分析

徐艺哲 万千 左光 石泳

大型航天器无控再入气动稳定性分析

徐艺哲 万千 左光 石泳

（北京空间技术研制试验中心，北京 100094）

大型航天器在轨运行寿命终止后，为避免坠落在人口稠密地区造成事故，一般通过控制其主动离轨再入，使其坠落在南太平洋航天器坟场区域。再入大气层过程中受气动作用影响剧烈，航天器气动稳定性对再入姿态及姿态保持有直接影响，从而影响到再入轨道。为分析质心位置、航天器舱外部件等对航天器气动稳定性的影响，文章利用快速气动力方法，获得了航天器在不同工况下的气动力矩特性，进而分析其气动稳定性。对于给定质心位置的航天器，随着舱外部件不断解体，从单配平点转变为多配平点。而对于不同质心位置，质心位置接近端面时仅存在单配平点，位于中部则可能出现多配平点。因此，对于需要再入的大型航天器，其质心位置及舱外部件在设计阶段就应考虑其对再入气动稳定性的影响，始终保持在单配平点工况，以降低再入过程姿态、轨道控制技术难度。

舱外部件 配平点 气动稳定性 受控再入 无控陨落

0 引言

运行于低轨道的大型航天器如空间站、大型卫星等由于大气顶层微弱阻力的影响，轨道高度不断衰减。在此类航天器正常运行时，需要通过发动机定期抬升轨道以维持轨道高度。若任由航天器寿命到期，轨道自然衰减再入大气层，航天器再入姿态、轨迹、落点均不可控[1]，存在解体碎片坠落在人口密集区，造成事故的风险[2-5]。各国对航天器/空间碎片再入过程开展了相应的预测方法研究[6-9]，但为了进一步降低风险，各国对于低轨大型航天器，均希望采用受控再入的方式，在航天器寿命即将结束时，主动减速离轨，可控地坠落在南太平洋航天器坟场区域。

主动受控再入初期，气动特性对航天器受控再入的姿态、轨道影响小。随着轨道高度降低，大气密度升高，气动力、力矩对航天器的姿态、轨道等影响逐步增大。若航天器预定姿态不是气动稳定姿态，同时气动稳定力矩超出了姿控发动机能力，则航天器无法控制为预定的姿态，从而无法按照预定轨迹再入。再入高度较低后，太阳翼解体、天线解体等过程极大地改变了航天器外形及气动特性，进一步影响其姿态和轨道，从而影响其落点。

对于常规的返回舱飞行器，其再入过程中的气动特性[10-13]、气动稳定特性[14-15]、配平特性[16-17]等均有大量研究。文献[16]的研究结果表明，对于返回舱再入过程，在高空稀薄流区域，其气动俯仰配平攻角随高度的降低而减小。气动俯仰配平攻角的变化幅度受到质心位置、马赫数等多种因素的影响。

对于带太阳翼的大型航天器，文献[18]的研究结果表明，高度100km以上时，太阳翼在稀薄来流中受到的气动载荷很低。高度低于100km时受迅速增大的动压以及脱体激波和太阳翼的相互干扰影响，太阳翼所受气动载荷明显增大。同时在相同高度下，太阳翼所受气动载荷与太阳翼的姿态角度直接相关。太阳翼气动载荷大时，将直接影响到航天器的气动稳定性。

实际再入过程中，航天器舱外部件受迅速增大的气动载荷影响，不断烧蚀、解体。航天器的质心和外形都处于不断变化的过程中，目前尚少见针对此过程中气动稳定性变化的相关研究。本文利用快速气动力计算方法，系统分析了大型航天器再入过程中随舱外部件解体带来的不同构型及质心位置对气动稳定性的影响，能够为类似的大型航天器设计提供参考。

1 航天器外形及气动特性计算方法

1.1 航天器气动外形

本文基于某型号航天器的简化气动外形开展计算。简化气动外形包括大小舱段及天线、太阳翼等舱外大尺寸部件。航天器本体坐标系以航天器小端端面圆心为原点，轴指向大端圆心，轴在纵向对称面内垂直于轴，轴平行于太阳翼轴线，轴构成右手直角坐标系。在该坐标系中，航天器俯仰力矩按右手定则沿轴正方向，正的俯仰力矩使图1中航天器大端向上抬起；航天器偏航力矩按右手定则沿轴正方向，正的偏航力矩使图1中航天器大端向左转动。

定义航天器本体坐标系内气流速度矢量与平面的夹角为侧滑角，速度矢量在平面内投影与轴夹角为攻角0°攻角、侧滑角为0°时，航天器本体坐标系中气流速度矢量沿轴正向，即航天器小端向前飞行。航天器本体坐标系中，速度矢量的各个分量V、V、V和攻角、侧滑角的关系可表示为

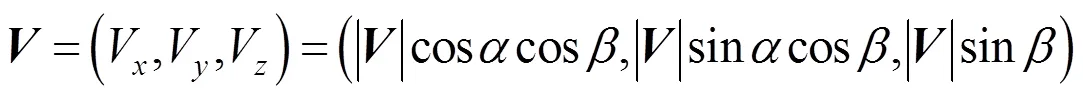
式中 攻角范围为–180°~180°，同时后文中为保证绘图连续，–180°~0°攻角范围也可表达为180°~360°；侧滑角范围为–90°~90°。

再入初期轨道高度高，空气稀薄，气动载荷小，随再入过程高度降低，气动载荷增大，太阳翼、天线等舱外大尺寸部件陆续解体，使得航天器主体气动外形发生变化。

针对以上外形，绘制三角形非结构表面网格用于计算气动特性，如图2所示。网格在局部细节处均进行了加密。

图1 某型号航天器简化气动外形

图2 航天器面网格示意

1.2 航天器气动特性计算方法

对于航天器再入过程，其马赫数可达20以上，同时由于高度较高，大气稀薄，通常使用工程计算方法以快速获得气动特性[19-23]。本文使用自由分子流–桥函数–修正牛顿流方法快速获得航天器气动特性。

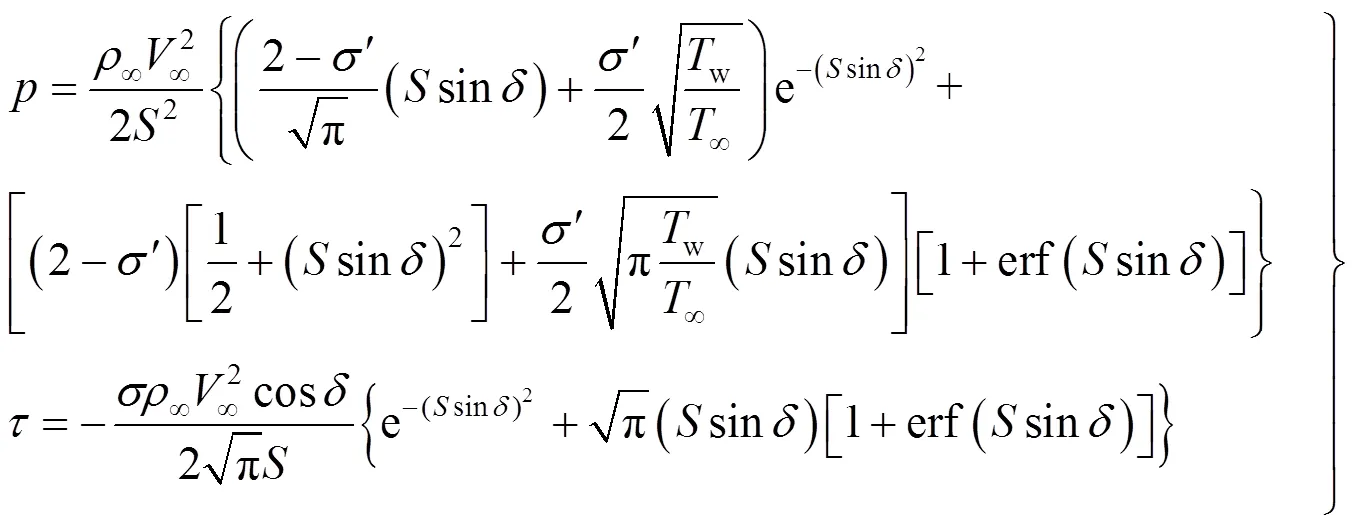
式中m是气体分子的最可几速度；是玻尔兹曼（Boltzmann）常数；是分子质量。

随再入过程高度降低，大气密度增大，减小，由自由分子流区进入过渡流区，可采用桥函数方法，将航天器在连续流区及自由分子流区的气动特性系数通过相关的代数桥函数加以组合，获得过渡流区气动特性。本文采用了文献[21]提出的工程上常用的用于过渡流区气动力估算的误差桥函数。

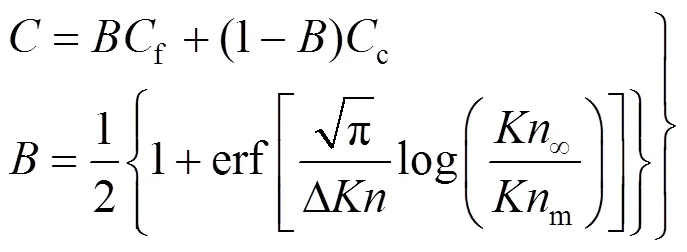
随高度进一步降低，进入连续流区后，对于来流马赫数≥15的来流，压力载荷占主导地位，粘性载荷可以忽略，采用修正牛顿流方法，可较好地获得航天器表面的无粘压力分布，进而获得气动特性。

2 气动稳定性分析

本章节对航天器气动稳定性仿真结果开展分析与讨论，分析了航天器再入阶段不同舱外部件、不同质心位置等方面的影响。根据某航天器典型再入过程中的构型、质心位置及弹道参数，给出计算状态如表1所示。

表1 计算工况

Tab.1 Calculation conditions

注：标称质心位置为航天器本体坐标系中质心坐标，即质心距航天器小端面距离，与航天器总长度的比值。

2.1 不同舱外部件的气动稳定性分析

首先，对带太阳翼、天线等舱外大型部件的某型号航天器的标称质心位置下的气动特性开展计算。绘制攻角-侧滑平面上的俯仰偏航力矩作用图，如图3。图中矢量方向代表俯仰、偏航力矩作用在航天器上带来的攻角、侧滑角变化效果。俯仰、偏航力矩为0的点根据矢量汇聚、发散可分为稳定配平点、鞍点及不稳定配平点三类。稳定配平点处周围矢量均指向该点，即任何扰动后气动力矩均使航天器姿态回到该点。而鞍点则在某些方向受扰动后会回复该点，但另一些方向受扰动后会远离该点。不稳定配平点则受扰动后即离开该点。例如：攻角250°侧滑–50°时，矢量指向右下方，代表力矩作用使得侧滑角增大，攻角减小，最终汇聚至攻角180°，侧滑角0°稳定配平点处。

图3 完整构型力矩作用图

如图3所示，大端向前，太阳翼在后时，存在一个稳定配平点，为攻角177.5°、侧滑角0°，且在整个攻角90°~270°、侧滑角–90°~90°范围内均趋向该配平点。而小端朝前时，仅具备一个不稳定配平点攻角–5.8°、侧滑角0°。从而航天器有且仅有一个稳定配平点，大端向前太阳翼在后，攻角177.5°、侧滑角0°，太阳翼起到了类似于气动安定面的配平作用。

其次，对太阳翼已解体、天线尚未解体航天器的标称质心位置下的气动特性开展计算，绘制攻角—侧滑角平面上的俯仰偏航力矩矢量图，如图4所示，局部放大图如图5。

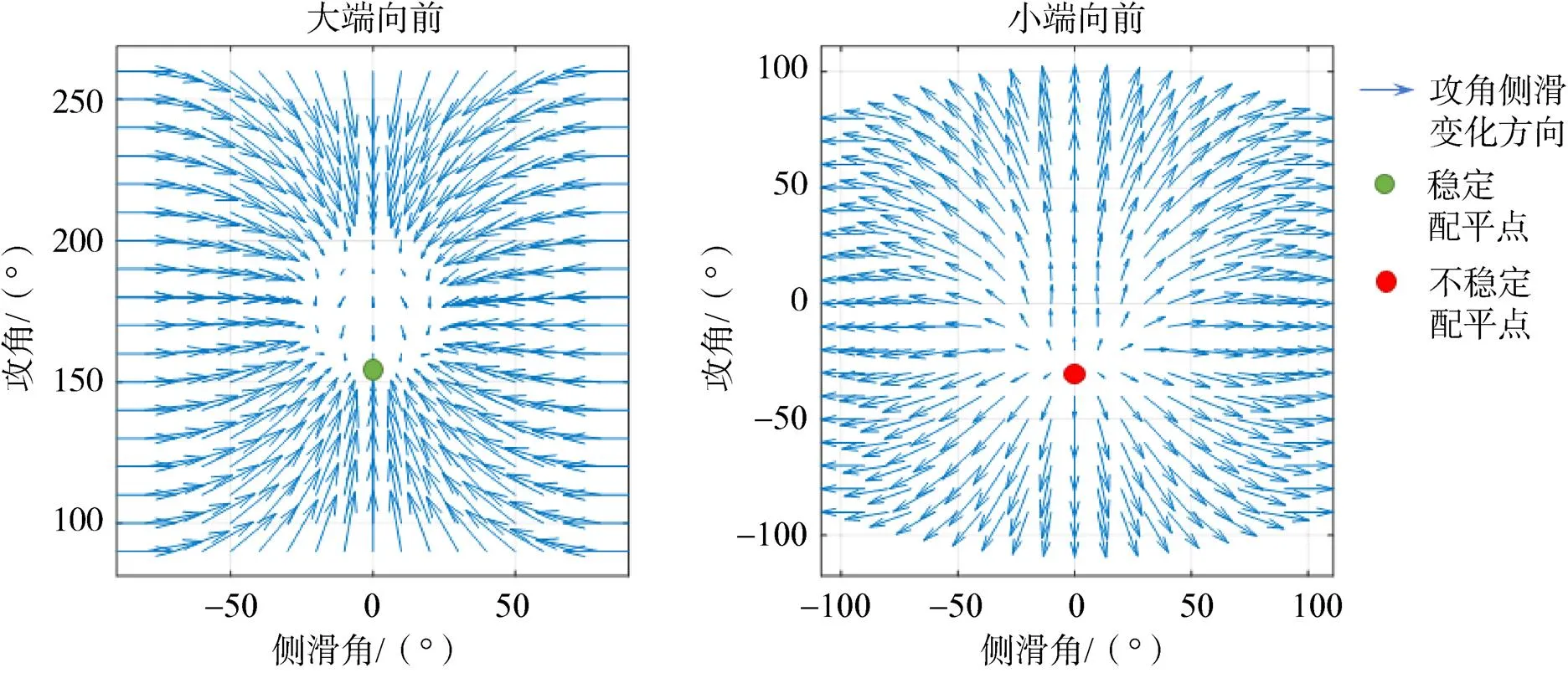
图4 太阳翼解体构型力矩作用图

图5 太阳翼解体构型力矩作用图局部细化

根据图4、图5，航天器小端向前时仅具备攻角–28°、侧滑角0°的一个不稳定配平点。大端向前时，具备攻角154°、侧滑角0°的一个稳定配平点。同时在攻角150°~200°、侧滑角–20°~20°范围内，航天器在气动力的作用下，会先倾向于向侧滑角±20°偏转，再向稳定配平点偏转，这是受天线等大型舱外部件的影响。

第三，对所有舱外部件均解体的航天器的标称质心位置下的气动特性开展计算，在纵向对称面内，攻角—俯仰力矩系数曲线如图6所示。

在攻角–20°、0°、20°、158°、180°、202°六处俯仰力矩系数均为0，其中0°、158°和202°为稳定配平点，其余为不稳定配平点。进一步分析得到攻角–侧滑角平面上的俯仰偏航力矩矢量，如图7所示，局部放大如图8。

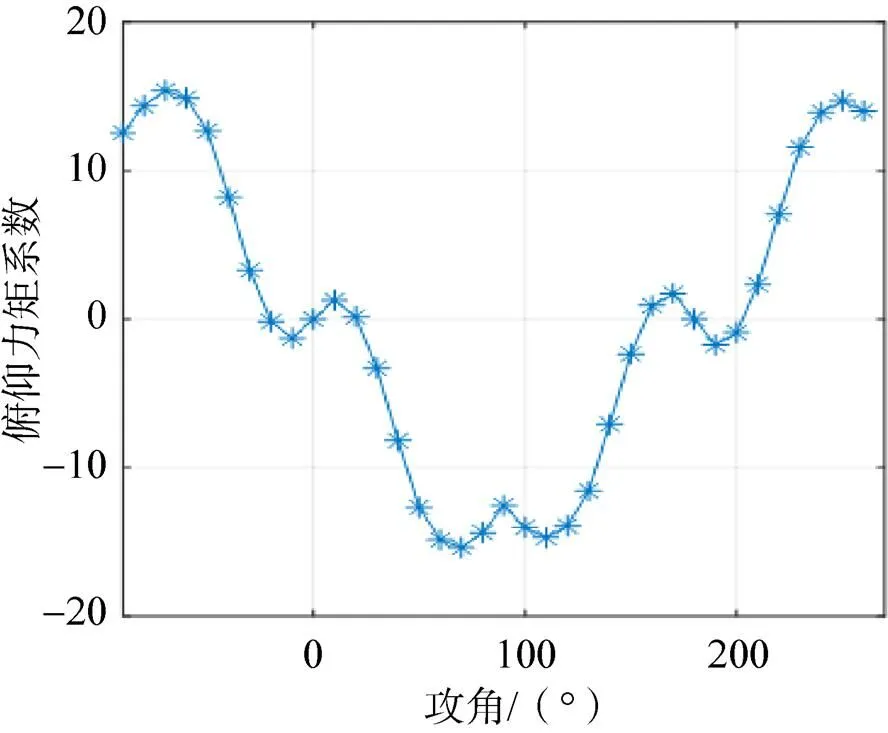
图6 舱外部件均解体构型0侧滑工况俯仰力矩系数随攻角变化曲线

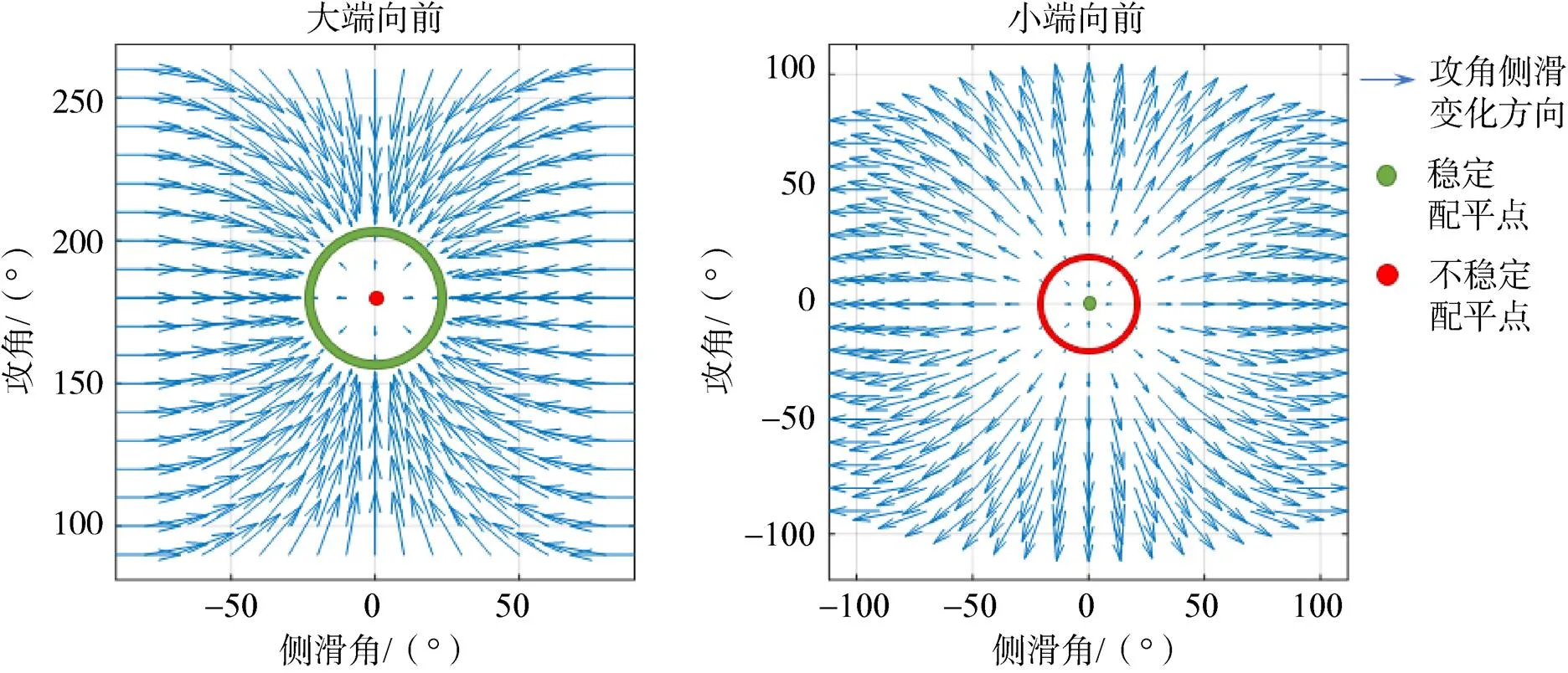
图7 舱外部件均解体构型力矩作用图

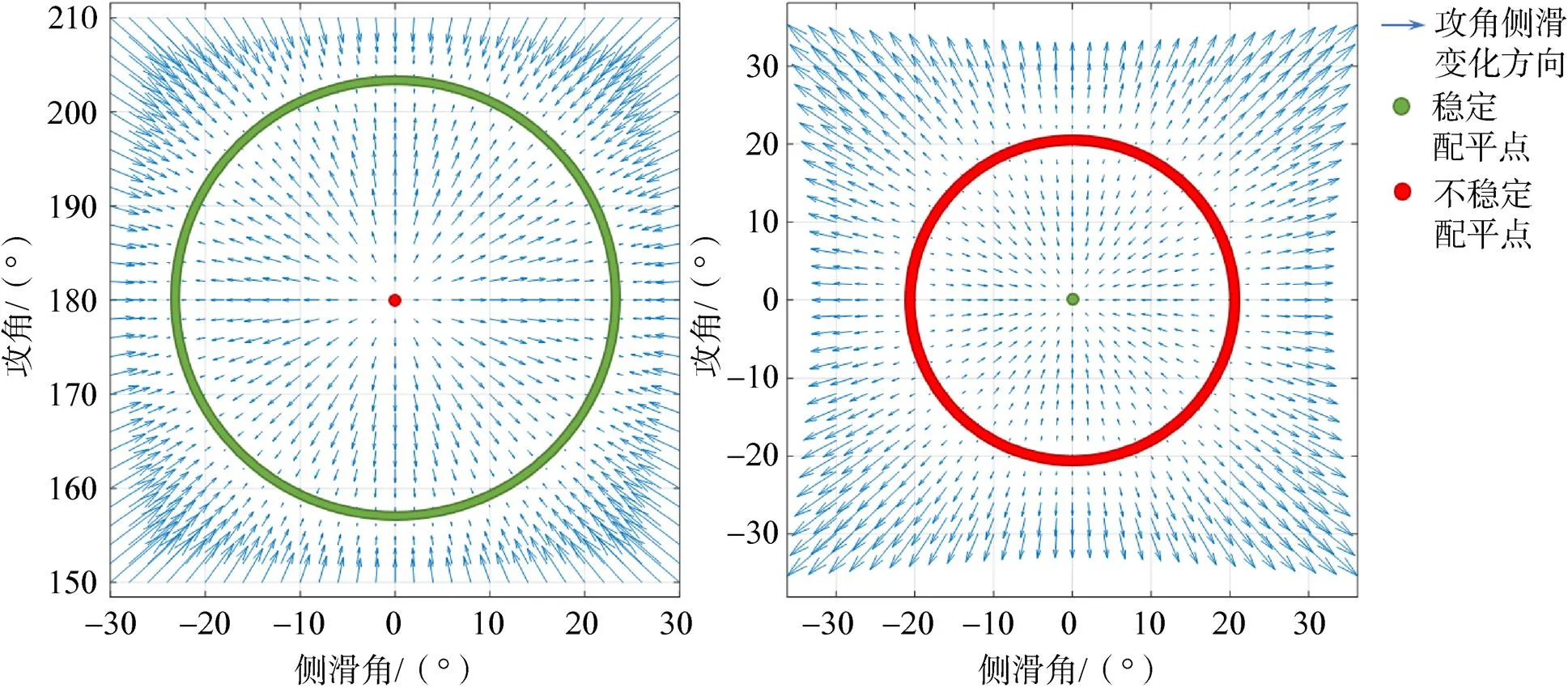
图8 舱外部件均解体构型力矩作用图局部细化

此时由于航天器变为轴对称构型，因此可在大端向前，速度与轴成22°夹角的一整组条件下均保持配平，而小端向前攻角为0°时亦为稳定配平点，但一旦扰动较大使得与轴夹角超过20°，即转向大端向前的姿态，如图8。此时若受扰动有一定的滚转速度，则由于绕轴旋转，只要保证大端向前，速度矢量与轴成22°角时均可配平，在无控情况下会导致不可预测的侧向及法向气动载荷。

2.2 质心位置对气动稳定性的影响

对该航天器，研究质心位置从小舱端面（0%）移动至大舱端面（100%）过程中，质心位置对气动稳定性的影响。对于完整构型，气动配平点位置随质心位置变化关系如图9所示；对于太阳翼解体构型，气动配平点位置随质心位置变化关系如图10所示；对于舱外部件均解体构型，气动配平点位置随质心位置变化关系如图11所示。

图9 完整构型配平点位置随质心位置变化

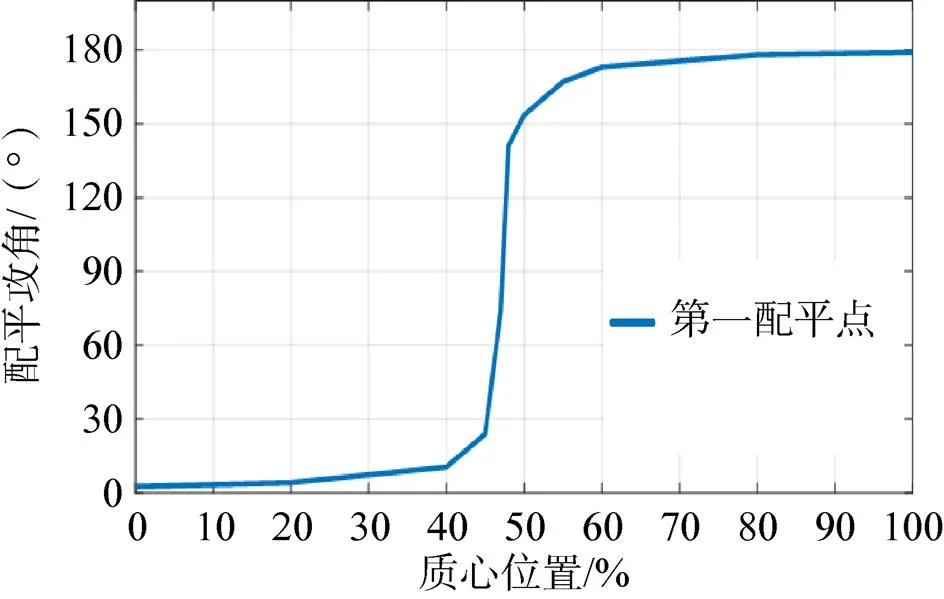
图10 太阳翼解体构型配平点位置随质心位置变化

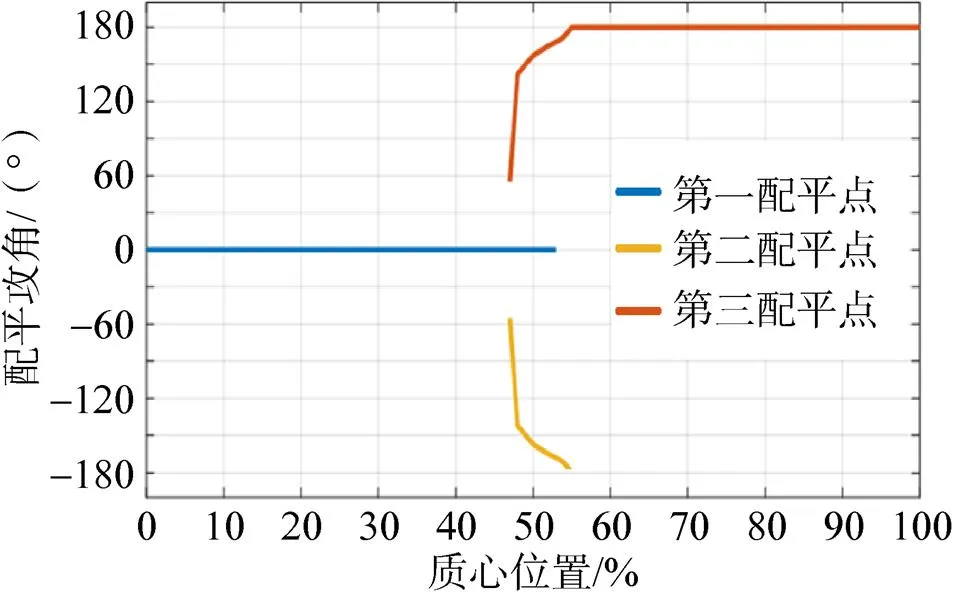
图11 舱外部件均解体构型配平点位置随质心位置变化

对于完整构型，质心位于全长0%~31%时，仅有攻角0°附近的第一配平点，对应小舱向前的姿态，如图9所示。质心位于全长36%~100%之间时，仅有攻角180°附近的第二配平点，对应大舱向前的姿态。值得注意的是，质心位于全长30%~36%之间时，航天器既可小舱向前配平，又可大舱向前配平，同时还出现了一个额外的大舱向前的第三配平点，这对再入方案的设计带来了一定的困难。

对于太阳翼解体构型，质心位于全长的位置从45%移动至50%时，飞行器从小舱向前配平迅速翻转至大舱向前配平，如图10。考虑到此阶段气动载荷已经较大，若实际质心恰好在此范围附近，则姿控发动机可能无法保持航天器姿态受控，导致航天器被气动载荷强行翻转，从而姿态、轨迹与设计出现较大偏差。

对于舱外部件均解体构型，质心位于全长0~47%间时，仅有小舱向前0°攻角的第一配平点，质心位于全长55%~100%间仅有大舱向前攻角180°的第三配平点，如图11所示。而质心位于全长47%~55%时，存在多个配平点，且根据2.1节分析配平点实际取向可以不在纵向对称面内。此时气动载荷很大，有可能导致航天器受到较大的侧向气动载荷，导致再入轨迹较大的侧向偏离。

根据以上分析，航天器受控再入过程中，假设质心位于全长49%处，该完整构型若按小舱向前配平控制，随高度下降动压迅速增大，太阳翼解体前后即可能导致航天器被气动载荷强行翻转至大舱向前，无法按预定轨迹再入，高度进一步降低全部舱外部件解体后，还有可能出现较大的侧向气动载荷，导致再入轨迹横向偏离，带来较大的空间碎片陨落风险。

3 结束语

本文基于快速气动方法，分析了航天器再入过程中舱外部件、质心位置等对气动稳定性的影响。分析结果表明，对于给定质心位置的航天器，再入过程中随舱外部件不断解体，气动稳定性从单配平点向多配平点转变，质心位置在航天器中部时，复杂的配平特性可能导致航天器发生剧烈的翻滚，从而给再入过程姿态、轨迹控制带来巨大风险。对于其他形式的大型航天器，再入过程中同样可能出现类似的气动多配平点的状态，可以采用本文所采用的方法加以研究分析。本文所采用的快速气动方法能够对航天器的气动稳定性进行快速分析，为航天器设计提供重要的参考依据，但该方法在定量处理复杂外形上还存在一定的不足，后续可以考虑在本文基础上，对于类似于多配平点、鞍点的工况，采用高精度的直接模拟蒙特卡洛方法或玻尔兹曼方程求解等方法加以更深入的研究。

[1] AILOR W. Spacecraft End-of-Life Disposal[M]//Encyclopedia of Aerospace Engineering. John Wiley & Sons, Ltd., 2010.

[2] 都亨, 张文祥, 庞宝军, 等. 空间碎片[M]. 北京: 中国宇航出版社, 2007: 1-128.DU Heng, ZHANG Wenxiang, PANG Baojun, et al. Space Debris[M]. Beijing: China Astronautic Publishing House, 2007: 1-128. (in Chinese)

[3] BOUSLOG S A, ROSS B P, MADDEN C B. Space Debris Reentry Risk Analysis[C]//Proceedings of 32nd Aerospace Sciences Meeting and Exhibit. Reno, NV, USA: AIAA, 1994.

[4] MILLARD S, ACONCHEN F. Risk Considerations for the Random Reentry of Space Debris[R]. AIAA 2010-1544, AIAA, 2010.

[5] PATERA R P. Hazard Analysis for Uncontrolled Space Vehicle Reentry[J]. Journal of Spacecraft and Rockets, 2008, 45(5): 1031-1041.

[6] CROWTHER R. Space Debris—Orbit Decay and Re-entry Prediction in Theory and Practice[C]//Proceedings of the 2nd AAS/AIAA Meeting. Colorado Springs, CO: AIAA, 1992: 967-981.

[7] WU Ziniu, HU Ruifeng, QU Xi, et al. Space Debris Reentry Analysis Methods and Tools[J]. Chinese Journal of Aeronautics, 2011, 24(4): 387-395.

[8] 胡锐锋, 龚自正, 吴子牛. 无控航天器与空间碎片再入的工程预测方法研究现状[J]. 航天器环境工程, 2014, 31(5): 548-557. HU Ruifeng, GONG Zizheng, WU Ziniu. Engineering Methods for Reentry Prediction of Uncontrolled Spacecraft and Space Debris: the State of the Art[J]. Spacecraft Environment Engineering, 2014, 31(5): 548-557. (in Chinese)

[9] LEE D J, CHOI E J, CHO S, et al. Effective Computational Approach for Prediction and Estimation of Space Object Breakup Dispersion during Uncontrolled Reentry[J]. International Journal of Aerospace Engineering, 2018, 2018:1-16.

[10] MITCHELTREE R A, WILMOTH, R G, CHEATWOOD F M, et al. Aerodynamics of Stardust Sample Return Capsule[J]. Journal of Spacecraft & Rockets, 1999, 36(3): 429-435.

[11] 方方, 周璐, 李志辉. 航天器返回地球的气动特性综述[J]. 航空学报, 2015, 36(1): 24-38.FANG Fang, ZHOU Lu, LI Zhihui. Review of Aerodynamic Characteristics of Spacecraft during Re-entry to Earth[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(1): 24-38. (in Chinese)

[12] FRITSCHE B, KLINKRAD H, KASHKOVSKY A, et al. Spacecraft Disintegration during Uncontrolled Atmospheric Re-entry[J]. Acta Astronautica, 2000, 47(2): 513-522.

[13] TANG W, ORLOWSKI M, LONGO J, et al. Aerodynamic Optimization of Re-entry Capsules[J]. Aerospace Science & Technology, 2001, 5(1): 15-25.

[14] JOHNSON J E, STARKEY R P, LEWIS M J. Aerodynamic Stability of Reentry Heat Shield Shapes for a Crew Exploration Vehicle[J]. Journal of Spacecraft & Rockets, 2006, 43(4): 721-730.

[15] 袁先旭, 张涵信, 谢昱飞. 飞船返回舱再入俯仰动稳定吸引子数值仿真[J]. 空气动力学学报, 2007, 25(4): 431-436.YUAN Xianxu, ZHANG Hanxin, XIE Yufei. Numerical Simulation for Dynamic Stability in Pitching of Unfinned Reentry Capsule and Bifurcation with Mach Number Prediction[J]. Acta Aerodynamica Sinica, 2007, 25(4): 431-436. (in Chinese)

[16] 梁杰, 李志辉, 杜波强. 飞船返回舱再入稀薄流域配平特性研究[J]. 航天返回与遥感, 2013, 34(3):42-48.LIANG Jie, LI Zhihui, DU Boqiang. Research on Trim Features of Reentry Capsule in Hypersonic Rarefied Flow Regime[J]. Spacecraft Recovery & Remote Sensing, 2013, 34(3): 42-48. (in Chinese)

[17] 梁杰, 李志辉, 李齐, 等. 返回舱再入跨流域气动及配平特性数值研究[J]. 空气动力学学报, 2018, 36(5): 848-855.LIANG Jie, LI Zhihui, LI Qi, et al. Research on Aerodynamic and Trim Features of Reentry Capsule Across Multiple Flow Regime[J]. Acta Aerodynamica Sinica, 2018, 36(5): 150-157. (in Chinese)

[18] 梁杰, 李志辉, 杜波强, 等. 大型航天器再入陨落时太阳翼气动力/热模拟分析[J]. 宇航学报, 2015, 36(12): 1348-1355.LIANG Jie, LI Zhihui, DU Boqiang, et al. Modeling and Analysis of Solar Array Aerothermodynamics During Large Scale Spacecraft Reentry[J]. Journal of Astronautics, 2015, 36(12): 1348-1355. (in Chinese)

[19] 赵波, 黄飞, 程晓丽. 返回器稀薄区气动特性工程计算方法的应用研究[J]. 航天返回与遥感, 2014, 35(1): 6-12.ZHAO Bo, HUANG Fei, CHENG Xiaoli. Utilization of Engineering Calculation Method for Transitional Regime Aerodynamics[J]. Spacecraft Recovery & Remote Sensing, 2014, 35(1): 6-12. (in Chinese)

[20] POTTER J L, PETERSON S W. Local Bridging to Predict Aerodynamic Coefficients in Hypersonic, Rarefied Flow[J]. Journal of Spacecraft and Rockets, 1992, 29(3): 344-351.

[21] WILMOTH R G, BLANCHARD R C, MOSS J N. Rarefied Transitional Bridging of Blunt Body Aerodynamics[C]// Proceedings of 21st International Symposium on Rarefied Gas Dynamics. Marseille, France: NASA, 1998: 26-31.

[22] VASHCHENKOV P, IVANOV M, KRYLOV A. Numerical Simulations of High-altitude Aerothermodynamics of a Promising Spacecraft Model[C]//27th International Symposium on Rarefied Gas Dynamics, 2011: 1337-1342.

[23] 徐珊姝, 吴子牛. 一般超音速过渡区气动特性的桥函数方法[J]. 计算物理, 2009, 26(3): 362-370.XU Shanshu, WU Ziniu. Transitional Bridging of Supersonic Aerodynamics[J]. Chinese Journal of Computational Physics, 2009, 26(3): 362-370. (in Chinese)

Analysis of Aerodynamic Stability During Large-scale Spacecraft Uncontrolled Re-entry

XU Yizhe WAN Qian ZUO Guang SHI Yong

（Institute of Manned Space System Engineering, CAST, Beijing 100094, China）

After the end of orbital life of large-scale spacecraft, it is generally controlled to actively deorbit and complete its destructive re-entry in the Spacecraft Cemetery in the Southern Pacific Ocean, in order to avoid the risk of accidently depositing debris in populated areas. Aerodynamic effect is severe during the process of re-entry. The aerodynamic stability of spacecraft has direct impact on the reentry attitude and attitude hold, thus affecting the re-entry orbit. In this paper, the aerodynamic torque characteristics of the spacecraft under different working conditions are obtained by using fast aerodynamic methods, to analyze the influence of the centroid position and external components on the aerodynamic stability of the spacecraft. For spacecraft with given centroid position, as the external components disintegrate, the stability varies from one single neutral point to multiple neutral points. For different centroid positions, there is only a single neutral point when the centroid position is close to the end surface of the spacecraft, but multiple neutral points may appear when the centroid position is in the middle of the spacecraft. Therefore, for large-scale spacecraft, the centroid position and external components should be considered in the design stage in order to always maintain the aerodynamic stability at single neutral point, thus reduce the technical difficulty for re-entry control.

external components; neutral point; aerodynamic stability; controlled re-entry; uncontrolled re-entry

V411.4

A

1009-8518(2019)04-0001-09

10.3969/j.issn.1009-8518.2019.04.001

徐艺哲，男，1989年生，2016年获清华大学力学专业博士学位，工程师。研究方向为空气动力学及航天器总体设计。E-mail：davidhull@163.com。

2019-02-19

（编辑：庞冰）