基于粒子群算法优化的城市供水量预测模型研究

陈攀 杜坤 周明 毛润康 雷雨晴 丁榕艺

摘 要：鉴于BP神经网络、RBF神经网络在城市供水量预测精度上的不足，利用粒子群算法优化两者相关参数，实现更高预测精度，并通过建立BP神经网络、RBF神经网络、PSO-BP神经网络、PSO-RBF神经网络分别对城市供水量数据进行仿真预测。最终测试样本统计结果显示：RBF神经网络比BP神经网络平均相对误差（MRE）低约1%，在拟合度（R2）上高约0.014;PSO-BP神经网络比BP神经网络在MRE上降低约1.25%，在R2上提高约0.05;PSO-RBF神经网络比RBF神经网络在MRE上降低约0.3%，在R2上提高约0.072。由此说明RBF神经网络比BP神经网络在城市供水量预测方面更有优势，并且利用粒子群算法优化神经网络模型参数可有效提升神经网络预测精度。

关键词：粒子群算法;神经网络;供水量;相对误差;拟合度

DOI：10. 11907/rjdk. 191738 开放科学（资源服务）标识码（OSID）：

中图分类号：TP303文献标识码：A 文章编号：1672-7800（2019）007-0019-05

Research on the Prediction Model of Urban Water Supply

Based on Particle Swarm Optimization

CHEN Pan， DU Kun， ZHOU Ming， MAO Run-kang， LEI Yu-qing， DING Rong-yi

（Faculty of Civil Engineering and Mechanics， Kunming University of Science and Technology， Kunming 650500， China）

Abstract：In view of the shortage of BP and RBF neural networks in the prediction accuracy of urban water supply， the particle swarm optimization algorithm is used to optimize the related parameters to achieve higher prediction accuracy， and BP neural network， RBF neural network and PSO-BP are established. The neural network and PSO-RBF neural network respectively simulate and predict the urban water supply data. The final test sample statistics show that the RBF neural network is about 1% lower than the BP neural network average relative error （MRE）， and about 0.014 higher than the fitness （R2）; PSO-BP neural network ratio the BP neural network was reduced by about 1.25% on the MRE and about 0.05 on the R2; the PSO-RBF neural network was reduced by about 0.3% on the MRE than the RBF neural network， and the R2 was improved on R2 by 0.072. Therefore， it is shown that RBF neural network has more advantages than BP neural network in urban water supply forecasting， and using particle swarm optimization algorithm to optimize the parameters of neural network model can effectively improve the prediction accuracy of neural network.

Key Words： particle swarm optimization; neural network; water supply; relative error; fitting degree

基金項目：国家自然科学基金项目（51608242）;云南省应用基础研究青年项目（2017FD094）

作者简介：陈攀（1994-），男，昆明理工大学建筑工程学院硕士研究生，研究方向为市政工程;杜坤（1986-），男，博士，昆明理工大学建筑工程学院讲师，研究方向为智能优化算法、供水管网数值仿真等。本文通讯作者：杜坤。

0 引言

城市供水量预测在水厂水泵运行与优化调度中起着举足轻重的作用。准确可靠的供水量预测可提高市政供水管网稳定性与可靠性，并降低运行时产生的能耗，同时也是城市供水基础设施规划设计的关键[1]。

神经网络模型是近年研究热门，也是预测城市供水量的有效模型，但由于其中参数设置直接影响模型性能和预测精准度等，往往需要反复调试各个参数寻找最优参数设置，而粒子群算法（PSO）能够利用自身算法特点将神经网络中的某些参数进行优化，因此可以得到更优越的神经网络模型用于供水量预测。

班懿根[2]利用RBF神经网络对阿克苏市需水量进行预测，预测结果与实际需求吻合度较高，但当原数据不充分时，预测精度较低;温家鸣等[3]利用BP神经网络对桂林市需水量进行预测，精确度较高，但该神经网络易陷入局部最优解。

针对以上神经网络的缺点，许多学者利用粒子群算法进行参数优化：张志宇等[4]利用粒子群算法优化RBF神经网络参数，再对需水量进行预测，模型运行速度及预测精度得到了提升;徐瑾等[5]为了解决BP易陷入局部最优解的问题，利用粒子群算法优化BP网络连接权值及阈值，结果显示优化后的模型预测精度更高、更稳定;陈伟楠等[6]将主成分分析法、粒子群算法及BP神经网络相结合对泰州市供水量进行预测，结果显示该组合运行速度快、预测精度更高;商志根等[7]利用粒子群算法确定LS-SVM模型相关参数，相比于原模型，优化后的模型预测精度更高。

本文利用粒子群算法优化BP神经网络与RBF神经网络相关参数，并对某市供水量数据进行仿真预测，对比分析预测结果可知，该算法不仅可比较两者性能差异，还可对神经网络进行优化，克服神经网络应用的部分难点。

1 神经网络模型

1.1 RBF神经网络

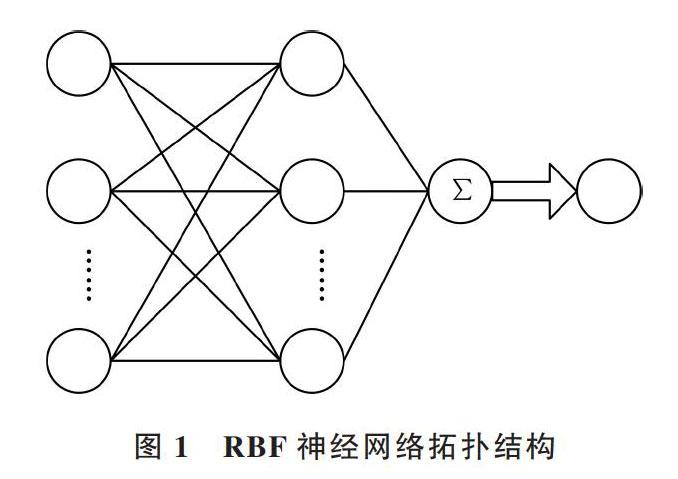
径向基（RBF）神经网络[8]是一个三层前向神经网络，具有一个单独隐层。如图1所示，第一层为输入层，输入层由信号源节点组成，仅用于传输信号;第二层是隐含层，利用非线性优化方法对输入向量进行变换，并将低维输入数据转换为高维空间，使低维空间非线性问题成为高维空间线性问题;第三层是输出层，使用线性优化策略调整线性权重。

图1 RBF神经网络拓扑结构

激活函数（径向基函数）[9]可表示为：

[R（Xi-Zi）=exp（-12σ2Xi-Zi2）]        （1）

网络输出[10]可表示为：

[Yi=i=1hWijexp（-12σ2Xi-Zi2）]        （2）

其中，[Xi]指第i个输入样本，[Zi]指隐藏层单元中心，[σ]指宽度，h指隐含层节点数，n指输出的样本数，W指隐含神经元至输出神经元的连接权值。

RBF应用难点在于网络训练，网络训练应正确选择和估计输入参数，包括基本功能的中心和宽度以及神经元连接权重。RBF神经网络隐含层至输出层的映射关系是线性的，而将向量由低维度映射至高维度就是隐含层的作用，由此在高维度中就变成线性可分。RBF网络在非线性与线性之间变化，使网络加快学习速度且避免陷入局部极小解的情况;预测模型中的特征预处理技术对预测精度也有显著影响，尤其是将神经网络与预处理的输入特征数据相结合，可以获得更好的预测精度。

本文利用MATLAB中的newrb函数进行建模。建模前需要预先设定训练参数，包括径向基函数扩展速度和均方误差目标。速度越大，函数逼近误差越大，但低速会导致网络性能下降。目标用于控制训练过程的终止。在训练过程中，中间层神经元数量不断增加，直至模型均方误差达到设定值（目标）。由于很难确定这两个参数的最佳值，本文利用PSO优化网络中的最佳训练参数（W，Z，σ 3个参数）使神经网络性能大幅提升。

1.2 BP神经网络

反向传播神经网络[11]（BP神经网络）是一种多层前馈人工神经网络，由Rumelhart & McCelland于1986年提出的误差反向传播算法训练而成。BP神经网络能够在数据输入前后学习和存储大量功能关系，若没有事先确定功能关系，只能通过数据训练。BP神经网络算法是一种监督学习算法，即若输出层的实际输出值与期望的输出值不匹配，将立即进行误差反向传播。该算法基于最小二乘法（LMS），采用逐层向前移动的方法，使输出值与期望值之间的误差平方在阈值范围内。换言之，BP神经网络通过反向传播修正网络权值和阈值，减小输出值和期望值之间的误差。BP神经网络结构包括输入层、隐含层以及输出层。

图2 BP神经网络拓扑结构

隐含层节点输出[12]为：

[Oj=f（∑Wij×Xi-qj）]        （3）

输出节点输出模型[13]为：

[Ym=f（∑Wjk×Oj-qk）]        （4）

其中，[Oj]指隐含层节点输出，f指非线性作用函数，[Wij]及[Wjk]指隐含层连接权值，[Xi]指输入值，[Ym]指输出值，[qj]及[qk]指神经单元阈值。

其中，PSO算法优化对象是BP神经网络中的W和q两个参数。

考虑到将数据归一化后可大幅提高神经网络性能，因此本文利用式（5）对原数据进行线性函数转换，再进行归一化处理。

[y=x-xminxmax-xmin]          （5）

其中，y指神经网络输出值;x指原始数据输入值;[xmin]指原始数据中的最小值;[xmax]指原始数据中的最大值。

BP神经网络具有网络结构简单、可操作性强、输入输出任意非线性拟合等优点，可用于图像识别、信息预测和模式识别等。

由式（6）可以大致确定BP神经网络的隐含层神经元个数最佳值范围[14]。

[h=（m+n）+a]          （6）

其中，h指隐含层神经元个数，m指输入层节点数，n指输出层节点数，a指1～10的常数。

2 粒子群算法

粒子群优化（PSO）算法是Eberhart & Kennedy[15]于1995年提出的一种基于种群的随机优化技术。PSO的发展灵感来自于动物群体的社会行为，如鸟群和鱼群。PSO与其它一些进化计算技术有许多相似之处：系统由随机解的总体初始化，并通过更新代数搜索最优解。在粒子群優化算法中，每个个体都被称为一个粒子，其行为就像鸟群（鱼群）中的一只鸟（或鱼）在寻找食物或躲避捕食者。每个粒子都有一个位置和一个速度，用来探索问题的搜索空间。一个位置代表一个潜在的问题解决办法。一个粒子从它自己的经验中学习（认知成分），也从群体中学习（社会成分）。通常，个人和社会成分分别称为Pbest（个体极值）和gbest（全局最优）。为了评估一个解，PSO迭代地计算每个粒子的适应度[16]。

这些粒子在超大型搜索空间中“飞行”。搜索空间中粒子位置变化是基于个体的社会心理激励原理。每个粒子的位置根据其经验和相邻粒子的经验变化。粒子群算法中的粒子作为候选解被引入。粒子执行迭代目的是找到具有目标函数最佳值的解。每个粒子都有一个由矢量[Xi]（其中，i是粒子的下标）表示的位置，速度则表示为[Vi]矢量。迭代过程中的每一个粒子均会记住自身在Pbest矢量中的最佳位置。粒子群中的最佳位置矢量存储在gbest中。每次迭代时速度矢量的更新根据公式（11）进行;然后，利用前一位置获得新的速度，根据公式（12）形成新的位置。

具体过程为：设在一个Z维空间里面，存在随机粒子N个，则第i个粒子的位置函数可表示为[17]：

[Xi=（Xi1，Xi2，？，XiZ）]            （7）

其中i=1，2，……N（下同）。

第i个粒子速度为：

[Vi=（Vi1，Vi2，？，ViZ）]          （8）

第i个粒子目前寻找到的个体极值为[18]：

[Pbest=（Pi1，Pi2，？，PiZ）]         （9）

则该Z维空间中的整个群落（粒子群）寻找到的最优位置即为全局极值，因此可由式（6）表示为：

[gbest=（Pg1，Pg2，？，PgZ）]        （10）

其中，粒子依据公式（11）、（12）更新自己的速度及所在位置[19]：

[ViZ=wViZ+c1r1（PiZ-XiZ）+c2r2（PgZ-XiZ）]   （11）

[XiZ=XiZ+ViZ]          （12）

其中，[c1、2]为学习因子[20]（加速常数），[w]为惯性因子，[r1、2]指0～1的均匀随机数。

算法具体步骤[21]如下：

Step1：设置好粒子群各项参数并且需要将各个粒子的位置及速度进行初始化。

Step2：计算各个粒子适应度值。

Step3：如果个体极值小于由Step2计算得到的适应度值，则使用适应度值替换掉个体极值。

Step4：如果全局极值小于Step2计算得到的适应度值，则会使用适应度值替换掉全局极值。

Step5：各个粒子根据式（11）及式（12）更新自己的速度以及位置。

Step6：粒子群算法会在达到停止条件时，停止继续寻找最优值，否则算法将会返回Step2。

当达到程序设置的最大迭代次数或找到整个群落（粒子群）寻找到的最佳位置，即全局极值[gbest]时停止粒子群算法。

3 数据准备

本文采用收集到的某城市日供水量数据（不考虑其它影响因素），数据范围由2004年1月1日-2005年2月3日，共计400个数值，并利用前5天的供水量值预测第6天的供水量值，若输入矩阵记为P，输出矩阵记为Y，第i天的供水量记为[Xi]，则可得：

P=[X1X2X3X4X5X2X3X4X5X6？？？？？X395X396X397X398X399]，Y=[X6X7？X399X400]

其中，本文将输入矩阵前365行数据作为网络训练数据，第366行-第395行数据共30行数据作为测试数据，输出矩阵前365行数据作为网络训练数据，第371行-第400行数据共30行数据作为网络测试数据。

4 模型构建

本文通过建立BP、RBF以及由PSO分别优化的两个神经网络进行模型训练及仿真测试。其中粒子群算法参数设置如下：C1=C2=2，迭代次数设为200次，种群规模设置为30，粒子最大速度取1，最小速度取-1，最大权值取0.9，最小权值取0.2，训练误差设为1e-9。算法达到设置最大迭代次数或达到设置训练误差时即停止寻找最优值。

4.1 仿真结果

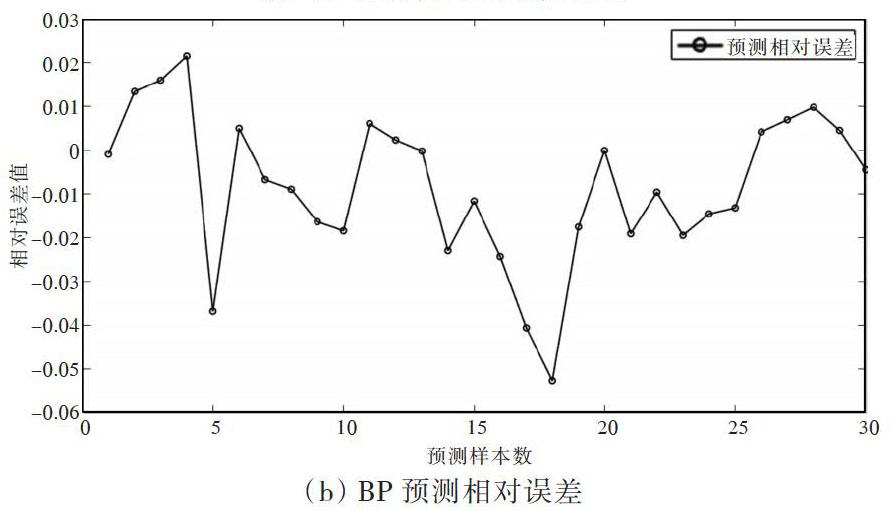
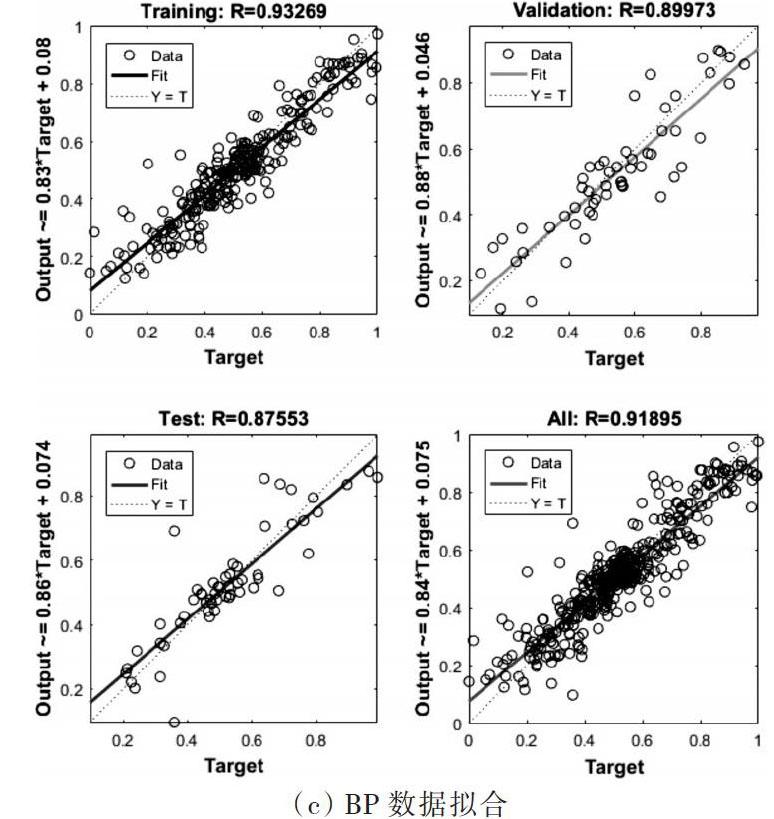
本文使用Matlab2016b软件进行模型训练以及仿真预测，分别建立BP、RBF、PSO-BP、PSO-RBF4种神经网络模型，预测得到的各项指标情况如图3及表1所示。

图3 各神经网络各项指标

图3中的数据拟合图为训练数据、验证数据、测试数据及所有数据拟合度，从中可以反映模型训练程度是否充分、模型是否可靠、有无过拟合等异常情况。由图3可知，本文建立的4个神经网络模型均为可靠有效的模型。

表1 相关指标统计结果

5 结语

本文使用粒子群算法对RBF与BP神经网络的相关参数进行优化，再利用MATLAB软件进行仿真模拟，最后对比优化前后神经网络的预测精度、预测误差、拟合度等指标。实验证明，粒子群算法能够提升神经网络的预测精度与拟合度，减小预测误差。但通过粒子群算法优化后的神经网络在预测精度方面仍有提高空间，这是下一步研究重点。

参考文献：

[1] 郭冠呈，刘书明，李俊禹，等. 基于双向长短时神经网络的水量预测方法研究[J]. 给水排水，2018，44（3）：123-126.

[2] 班懿根. 基于RBF神经网络的城市需水量预测[J]. 地下水，2012，34（1）：114-116.

[3] 溫家鸣，郭纯青，李新建， 等. 基于BP神经网络的桂林生态城市建设需水量预测[J]. 水资源保护，2012，28（3）：47-50.

[4] 张志宇，赵丹国，侯晓宇. PSO-RBF神经网络在城市需水量预测中的应用[J]. 水电能源科学，2013，31（6）：55-57.