机器学习的五大类别及其主要算法综述

李旭然 丁晓红

摘 要：机器学习作为一门源于人工智能和统计学的学科，是当前数据分析领域重点研究方向之一。首先通过追溯机器学习起源和介绍不同算法在求解策略上的启发性思路，讨论五类机器学习的发展及其主要算法在评价方法和优化方式上的实现，进一步总结归纳各算法适用领域和算法优劣，最后指出各算法克服自身缺陷的最新进展和未来实现多算法融合的研究方向。

关键词：机器学习;学习算法;集成方法;增强理论;元学习

DOI：10. 11907/rjdk. 182932 开放科学（资源服务）标识码（OSID）：

中图分类号：TP3-0文献标识码：A 文章编号：1672-7800（2019）007-0004-06

Survey on Five Tribes of Machine Learning and the Main Algorithms

LI Xu-ran，DING Xiao-hong

（School of Mechanical Engineering， University of Shanghai for Science and Technology， Shanghai 200093， China）

Abstract： Machine learning is a discipline derived from artificial intelligence and statistics， and it has been one of the key research directions in the field of data analysis. This paper introduces the inspiring ideas of different machine learning algorithms in the strategy through their origins， and the realization of five tribes of machine learning and the main algorithms including evaluation function and optimization method. Then applicable fields of each algorithm and both advantages and disadvantages of the algorithm are summarized. Finally this paper points out the latest progresses of each algorithm to overcome its own defects and the future research direction of multi-algorithm fusion.

Key Words： machine learning; learning algorithm; ensemble method; reinforcement learning; meta learning

作者简介：李旭然（1994-），男，上海理工大学机械工程学院硕士研究生，研究方向为智能设计;丁晓红（1965-），女，博士，上海理工大学机械工程学院教授、博士生导师，研究方向为机械结构多學科综合优化设计、智能化创新设计方法。

0 引言

机器学习源于人工智能和统计学[1]，在依次经历了两个10年的活跃与平静期后，1980年举办的首届机器学习国际论坛，标志着机器学习全面复苏。机器学习开始影响文明社会的各行各业，如消费领域自动驾驶、制造业异常检测、金融业统计分析和零售业在线推荐等。

定义学习机理作为机器学习的关键[2-4]，在发展史上先后出现了3种类型的论述方式。第一类论述的代表人物为Simon[5]，他指出学习是外部行为的变化，即系统通过学习作出自我改变，并在随后处理相近任务时变得高效;第二类论述的代表人物为Michalski[6]，他强调学习的内部过程，即学习是对经验事物表征的重构;而最后一类论述来自专家系统开发领域，其主要观点为获取知识即是学习[7]。

1 机器学习类别

按照学习态度和不同的灵感来源，可将机器学习大致分为5个具有不同思想的类别[8]，包括符号主义（Symbolists）、联结主义（Connectionists）、进化主义（Evolutionaries）、贝叶斯主义（Bayesians）和类推主义（Analogizer）。每个类别围绕各自的基本思想，有重点研究领域及相应算法。

符号主义认为，所有信息均可简化为操作符号，符号学者使用符号、规则和逻辑表征知识与进化逻辑进行推理，其主算法是逆向演绎，包括规则学习和决策树等;联结主义认为学习是大脑所做的事情，因此联结学者使用概率矩阵和加权神经元动态地识别和归纳模式，从而对大脑进行逆向演绎，其主算法是反向传播学习算法，如神经网络;进化主义从对自然选择的解释中发现了学习本质，它通过生成变化，再根据特定目标获取最优者，在计算机中实现对自然的模仿，其主算法是基因编程，如遗传算法;不确定性是贝叶斯主义关注的中心，其认为从知识获取过程到一切既定知识均具备不确定性。贝叶斯学者利用事件发生的概率大小进行计算，其主算法是贝叶斯定理，如朴素贝叶斯和马尔可夫链;类推主义从关系间的相似性着手，推导出其它关系。类推学者根据约束条件优化函数，通过找出需被记忆的经历并弄清之间的结合关系，实现新场景预测，其主算法是支持向量机。

表1 机器学习类别

在探寻新问题解的过程中，是否可让计算机记忆足够大量数据，然后从中寻找出解？答案是否定的。假设将被解答的新问题存储于数据库中，而现有数据库又非常庞大，则该问题出现的概率极低。记忆不能被当作学习算法。符号主义代表人物之一Tom Mitchell[6]察觉到必须在机器学习中预设观念，即引入附加假设，才可归纳出能力范围内最具普遍性的规则。另一个质问是如何在概括已知甚至未知的知识时，合理且准确？各类机器学习算法都在设法解答这一归纳性难点。符号主义创始人之一Ryszard Michalski[9]借鉴心理学中的“合取概念”对任意影响结果的因素进行组合，他设想在机器学习到任意一个规则后，用下一个规则尽可能多地包含剩余解，直到得到解对应的规则全集。但多数算法开始掌握的知识有限，这种“分而治之”的归纳算法很容易引起过拟合问题。对此，Stephen Muggleton等[10]借鉴“归纳是逆向演绎”的思路，于1988年设计出第一个归纳逻辑的程序。在面对海量数据时，符号学者提出决策树归纳，通过对规则的排序或让其选择解决多概念规则对应一个实例的问题，保证实例和规则一一对应，使决策树精度高且易于理解，Ross Quinlan[11]的研究使其成为分类问题的佼佼者。符号主义在1980年代迅速占据了机器学习的主导地位，并在专家系统的应用中大获成功，但又因为复杂的规则编码逐渐消失。随着人工智能技术的提升，上述先驱人物工作之间产生了新的联系，符号主义机器学习重新活跃起来[12-13]。

联结主义认为，符号主义仅通过逻辑规则定义概念的方式不足以掌握全部实例。联结主义信奉“同时被激活的神经元会被联系在一起”的赫布理论，反过来分析人类大脑的运转方式[14-15]。1960年前后Frank Rosenblatt[16]通过给McCulloch-Pitts神经元之间的连接赋予不同的权重设计感知器。感知器结构简单，仅借助例子训练即可区分图像声音。但如果遇到正负实例之间不能被超平面分离的情况，即典型的排斥-或功能（exclusive-OR function， XOR），感知机则不能进行学习。直到1985年同时具有感官和隐藏神经元的玻尔兹曼机器的诞生，将联结主义的复兴带到顶峰。虽然玻尔兹曼机器有效解决了贊誉分布问题，但在实践过程中学习行为开展得异常缓慢和艰难。此后不久，Yann LeCun[17]发现了一个既能学习XOR，又能高效处理赞誉分布问题的反向传播算法，并与Yoshua Bengio等[17-18]对其不断优化。深度学习算法诸如叠加自动编码器、卷积神经网络的诞生让联结主义一度成为机器学习的主导思想。

进化主义和联结主义一样，都试图效仿自然进行学习的方法。John Holland[19-20]最早研究的是神经网络，但随着关于进化的数学理论体系逐渐成熟，其关注点转变为一种从达尔文自然选择理论转化的算法。遗传算法类似选择育种，它通过模拟点突变和染色体交叉过程生成变化，然后引入适应度函数给程序和目标的契合度打分。在解决垃圾邮件过滤的应用过程中，他提出分类器系统的规则集，并利用桶队算法处理其面临的赞誉分布问题。尽管如此，与分层感知器相比，分类器系统可适用的领域十分有限。1987年John Koza[21]发现了基因编程方法，即对成熟的计算机程序自身进行进化。这种对程序树而非字符串进行交叉的方法，使学习活动变得更为灵活。目前联结主义最引人关注的应用是具有自我意识和创造力进化的机器人研发。反观进化主义和联结主义主算法的不同侧重点，前者注重结构学习，而后者则通过权值学习解决大部分工作。借助遗传算法寻找神经网络最优结构将成为两种思想的融合点。

与效仿自然的方法截然不同，贝叶斯主义和符号主义都试图从基本原理中探寻算法学习方式。贝叶斯主义基于贝叶斯定理，发明了朴素贝叶斯分类器，由于它可以获取输入输出间的两两相关关系而被广泛应用，最成功的案例之一是David Heckerman[22]的垃圾邮件过滤器。不论是朴素贝叶斯法还是马尔可夫链，均为贝叶斯网络特例，后者是由Judea Pearl[23-24]在20世纪80年代创建的一个关系图谱，包含任意的结构特征，且特征之间允许出现干涉。随之而来的是使变量呈指数性增大的推理问题，Pearl & Jordan[24-26]分别提出了“环路信念传播”思想和优化易于处理的分配内参数的方法进行近似推理。

上述4个类别的一个共同缺点在于，它们学习研究的显式模型在数据不充足的情况下无法继续有效。但类推主义却可以仅从小数据中进行学习，包括高效的最近邻算法和准确的支持向量机。Peter Hart等[27]创建的最近邻算法也被算作懒惰学习算法之一，它将每个数据点变成微型分类器，每次仅构建局部模型，其优点为学习过程简单、快速，但是也使其受“维数灾难”的影响比所有其它学习算法大。直到20世纪90年代，Vladimir Vapnik等[28-29]开发出的支持向量机成为类推主义新代表，支持向量机与加权k最近邻算法很像，但前者能够提供平缓的边界且不产生过拟合。Douglas Hofstadter[30]对类比推理学习评价颇高。

2 机器学习主算法

2.1 决策树

符号主义的主算法是决策树（Decision Tree）。作为一类模仿人脑在日常生活中处理决策问题的方法，决策树具有如面对“是否”、“好坏”等二分类任务的二叉树结构[30-32]。在得到问题结论即最终决策的过程中，所有对数据[（x，y）]中各特征[a]子决策判断的累积，使求解范围不断缩小。通常而言，一棵完整的决策树由一个包含数据和特征全集的根节点、若干代表特征判定的过程节点以及相应代表决策结果的叶节点组成。从根节点到叶节点的过程参照“分而治之”的机制展开，如图1所示。

图1 决策树学习策略

其中，决策树学习的核心问题之一是特征划分。3种经典划分方法形成了决策树的3种代表性算法：ID3、C4.5和CART（见表2）。

表2 决策树算法

剪枝是决策树学习的第二个核心问题，按照决策树生成与否分为先、后两种剪枝方式，以解决数据过拟合带来的后果，见表3。

表3 避免过拟合策略

2.2 人工神经网络

联结主义主算法是人工神经网络（Artificial Neural Networks，ANN）。以神经网络中的最小单元，即经典M-P神经元模型为例[33-34]，当前神经元收到来自前方神经元输出信号[X]加上权值[ω]后的信号，借助响应函数[f]如Sigmoid函数产生最终输出信号[Y]，与阈值[θ]对比的结果如图2所示。

图2 经典神经元模型

在神经网络发展过程中出现了前馈神经网络和递归神经网络[8]两种结构。后者打破了前者关于输入和输出相互独立的假设，通过网络建立的环形结构使某些输出信号反馈成为输入信息，见表4。

表4 神经网络类别

同时，误差反向传播（Error Back Propagation，BP）算法[9]既可以用在前馈神经网络，又可以用于递归神经网络训练，并得到最广泛的使用。以BP算法训练的m输入n并输出单隐层前馈神经网络为例，其拓扑结构见图3。

图3 单隐层BP神经网络拓扑结构

其中，[ωij]为输入层节点[i]和隐含层节点[j]之间的权值，[ωjk]为节点[j]和输出层节点[k]之间的权值。记[Oi]为节点[i]的输出（数值上等于[Xi]），[Netj]为节点[j]的输入，[h]为隐含层节点数，得到神经网络输出为：

记网络输出[Yk]与期望输出[Yk]的均方误差为[Ek]，学习率[η]，基于梯度下降法，有隐藏层节点[j]和输出层节点[k]之间的权值增量计算公式为：

其中[δk=（Yk-Yk）f（Netk）]，同理得到输入层节点[i]和隐含层节点[j]的权值增量[△ωij]和[δj]，从而BP神经网络建模流程如图4所示。

图4 神经网络建模流程

2.3 遗传算法

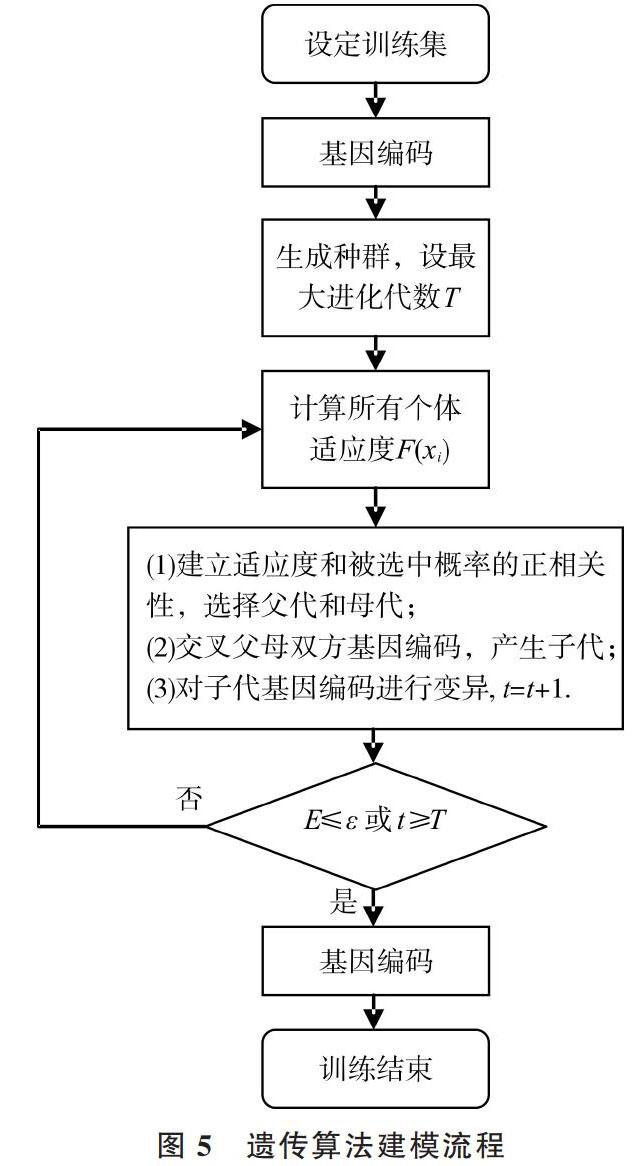
进化主义主算法是遗传算法。遗传算法努力避开问题的局部解，并尝试获得全局最优解，其基本思想来自达尔文物竞天择观和遗传学三大定律[35]。具体做法包括设计对问题解的编码规则，利用适应度函数和选择函数剔除次优解，再借助“交叉重组”及“变异”方法生成新的解，直到群体适应度不再上升，见图5。

图5 遗传算法建模流程

其中，迭代终止条件是群体适应度最大值与平均值相差E小于容差[ε]或迭代次数[t]超过最大进化代数[T]，表达个体适应度[F]和其被选中概率[P]的常用公式为：

值得注意的是，基因编码方式的合理选择对遗传算法效果影响显著，常见编码方式及特点见表5。

表5 遗传算法编码方式及特点

2.4 朴素贝叶斯

贝叶斯主义主算法是朴素贝叶斯算法[36-37]。源于统计学的贝叶斯定理可以表示为：

P（原因|结果）=P（原因）×P（结果|原因）/P（结果）

面对多分类问题，用训练数据[X]代替上式“结果”，用离散的数据特征种类[C]代替“原因”。为方便得到条件概率[Pxc]，忽略各特征间对分类作用的关联，此时有：

[Pcx=PcPxcPx=PcPxi=1dPxic] （4）

使样本按最低风险选择特征种类的最优分类判定准则有：

[H（x）=argmaxc∈CP（c）i=1dPxic]           （5）

其中[C]为特征种类[c]的取值集合，数量为[d]个。

但由于实际应用中各特征很可能相互干涉，且训练数据有缺失，于是又从中演化出其它算法，以增强泛化能力，见表6。

表6 贝叶斯算法及改进

2.5 支持向量机

类推主义的主算法是支持向量机。找到合理划分数据的超平面是该算法基本思想[38]（见图6）。

图6 超平面和间距

其中法向量[ω]和常量[b]通过分别定义超平面的方向与其到原点的距离，使该超平面被唯一确定。此时问题核心为两“支持向量”的间距[γ]最大化。经处理后得到数学优化模型为：

其中训练集[D]内[yi]的取值为[±1]。为了更高效地计算，通过例如Sequential Minimal Optimization （SMO）算法，求解由拉格朗日乘子法和Karush-Kuhn-Tucker （KKT）条件转化得来的式（6）之对偶问题。

若去除上述讨论中数据是线性可分的假设，则需引入核函数[κ（xi，xj）]将问题简化。该技术采用升维思想，通过非线性映射[φ（？）]，将原始数据如二维空间转化成更高维的三维空间，即可在高维特征空间中使数据线性可分，并按相似步骤求解。值得注意的是，核函数的函数选取对能否接近问题的最优解有很大影响。依据经验首先试用高斯核函数。

支持向量机的功能包括处理分类（Support Vector Classify，SVC）问题和回归（Support Vector Regression， SVR）问题两种。本文着重讨论其分类功能，而两者主要差异在于数学模型。对于回归问题，此时训练集[D]内[yi]属于实数域。若训练数据与回归函数之间的偏差不超过[ε]即被算法采纳，见图7。

图7 支持向量回归原理

此时，回归问题的数学模型可转化为：

其中[C]为正则化因子，[ξi]和[ξi]为函数两侧松弛因子。

3 结语

机器学习各类别代表方法、评价及优化部分总结如表7所示。

符号主义主算法决策树可以处理机器学习的分类任务和回归任务，优点包括学习效率高、解释性强，适用于具有不相关特征或特征缺失的场合，缺点包括无法考虑数据间的关联，易受数据在某特征内数量多少的影响发生过拟合。对此，现在多采用集成方法，如隨机森林（Random Forest，RF）克服决策树的缺点，提升学习准确度。

表7 各类别机器学习算法

联结主义的主算法为人工神经网络，可以处理机器学习回归任务，优点包括学习能力强，鲁棒性好;缺点包括需要做大量前期参数优化工作，学习效率低，学习过程不可知。但伴随着深层神经网络等深度学习算法的诞生，该方法在工程上得到了广泛应用。

进化主义的主算法是遗传算法，适用于解决最优化问题，相比传统方法如爬山法，可更有效地与其它机器学习算法结合，在神经网络中实现参数优化。其缺点是数学基础薄弱，缺乏完整的收敛理论。

贝叶斯主义的主算法朴素贝叶斯模型，可处理机器学习分类任务，优点包括数学基础坚实，学习能力强，适用于数据缺失的学习情景;缺点是要求数据量大，计算效率低。

类推主义主算法的支持向量机，可以处理机器学习分类任务和回归任务，优点包括数据需求量小，计算精度高，适用于高维特征空间和多输入多输出问题。但核函数选取和具体问题相关，缺乏明确规则，导致对缺失的数据处理效果差。

综上所述，各种类别的机器学习算法均有擅长的领域和难以克服的缺陷，其未来趋势是进一步融合，如完善集成方法[39-40]和增强理论[41-42]，或利用元学习（Meta Learning，ML）算法解决更深层次的学习“如何学习”的问题。

參考文献：

[1] 王珏，周志华，周傲英. 机器学习及其应用[M]. 北京：清华大学出版社，2006.

[2] 闫友彪，陈元琰. 机器学习的主要策略综述[J]. 计算机应用研究， 2004， 21（7）：4-10.

[3] 李世军. 非概率可靠性理论及相关算法研究[D]. 武汉：华中科技大学， 2013.

[4] 王光宏，蒋平. 数据挖掘综述[J]. 同济大学学报：自然科学版， 2004，32（2）：246-252.

[5] KOTSIANTIS S B， ZAHARAKIS I D， PINTELAS P E. Machine learning： a review of classification and combining techniques[J]. Artificial Intelligence Review， 2006， 26（3）：159-190.

[6] MITCHELL T M. Machine learning. [M]. 北京：中国机械出版社， 2003.

[7] ROBERT C. Machine learning， a probabilistic perspective[M]. Cambridge：MIT Press， 2012.

[8] DOMINGOS P. The master algorithm： how the quest for the ultimate learning machine will remake our world[M]. England：Reed Business Information Ltd.， 2015.

[9] ANDERSON J R，MICHALSKI R S，MITCHELL T M. Machine learning， an artificial intelligence approach[M]. Berlin：Springer，1984.

[10] MUGGLETON S，BUNTINE W. Machine invention of first-order predicates by inverting resolution[M]. Machine Learning Proceedings， 1988：339-352.

[11] QUINLAN J R. C4.5： programs for machine learning[M]. NewYork：Morgan Kaufmann Publishers Inc. 1992.

[12] DOMINGOS. Toward knowledge-rich data mining[J]. Data Mining & Knowledge Discovery， 2007， 15（1）：21-28.

[13] SILVER N. The signal and the noise[M]. New York：Penguin Press， 2012.

[14] SEUNG S. Connectome： how the brain's wiring makes us who we are[M]. Boston：Houghton Mifflin Harcourt Trade， 2012.

[15] MCCLELLAND，JAMES L. Parallel distributed processing[M]. Cambridge：The MIT Press， 1986.

[16] ANDERSON J A，ROSENFELD E. Neurocomputing： foundations of research[J]. Artificial Intelligence， 1992， 53（2-3）：355-359.

[17] LECUN Y， BOTTOU L， BENGIO Y， et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE， 1998， 86（11）：2278-2324.

[18] BENGIO， Y. Learning deep architectures for AI[J]. Foundations and Trends in Machine Learning， 2009， 2（1）：1-127.

[19] WALDROP，MITCHELL M. Complexity： the emerging science at the edge of order and chaos[M]. New York：Simon & Schuster， 1992.

[20] HARIK G R. The compact genetic algorithm[J].  IEEE Transactions on Evolutionary Computation， 1999， 3（4）：287-297.

[21] KOZA J R. Genetic programming： on the programming of computers by means of natural selection[M]. Cambridge：MIT Press，1992.

[22] HECKERMAN D. Bayesian networks for data mining[J]. Data Mining & Knowledge Discovery， 1997， 1（1）：79-119.

[23] DUDA R O，HART P E. Pattern classification and scene analysis[M]. New Jersey： Wiley， 1973.

[24] DARWICHE A. Modeling and reasoning with bayesian networks[M]. Cambridge：Cambridge University Press，2009.

[25] HOFF P D. A first course in bayesian statistical methods[M]. New York：Springer， 2009.

[26] MCGRAYNE S B. The theory that would not die：how bayes' rule cracked the Enigma code， hunted down russian submarines， and emerged triumphant from two centuries of controversy[M]. New Haven：Yale University Press， 2011.

[27] COVER T，HART P. Nearest neighbor pattern classification[M]. NewYork：IEEE Press，1967.

[28] QUINLAN J R. Induction on decision tree[J]. Machine Learning， 1986， 1（1）：81-106.

[29] CRISTIANINI N， SHAWE-TAYLOR J. An introduction to support vector machines[M]. Cambridge：Cambridge University Press，2000.

[30] HOFSTADTER D. The man who would teach machines to think[M]. Washington：The Atlantic， 2013.

[31] SURHONE L M， TENNOE M T， HENSSONOW S F， et al. Random forest[J]. Machine Learning， 2010， 45（1）：5-32.

[32] HUANG L，CHEN H，WANG X，et al. A fast algorithm for mining association rules[J]. Journal of Computer Science and Technology， 2000， 15（6）：619-624.

[33] DEMUTH H B，BEALE M H，JESS O D，et al. Neural network design[M]. 戴葵，李伯民，譯. 北京：中国机械出版社，2007.

[34] 李彦冬，郝宗波，雷航. 卷积神经网络研究综述[J]. 计算机应用，2016，36（9）：2508-2515.

[35] 吉根林. 遗传算法研究综述[J]. 计算机应用与软件，2004，21（2）：69-73.

[36] HOFF P D. A first course in Bayesian statistical methods[J]. Journal of the Royal Statistical Society，2010，173（3）：694-695.

[37] 王爱平，张功营，刘方. EM算法研究与应用[J]. 计算机技术与发展，2009，19（9）：108-110.

[38] 娄钰. 支持向量机算法研究[D]. 大连：大连理工大学， 2007.

[39] 董乐红，耿国华，高原. Boosting算法综述[J]. 计算机应用与软件，2006，23（8）：27-29.

[40] 于玲，吴铁军. 集成学习：Boosting算法综述[J]. 模式识别与人工智能，2004，17（1）：52-59.

[41] 孙志军，薛磊，许阳明，等. 深度学习研究综述[J]. 计算机应用研究，2012，29（8）：2806-2810.

[42] LECUN Y，BENGIO Y，HINTON G. Deep learning.[J]. Nature， 2015， 521（7553）：436-444.

（责任编辑：江 艳）