螺旋输送机设计与螺旋体有限元分析

王云先

（中铝山东工程技术有限公司，山东 淄博 255052）

1 设计参数

螺旋输送机结构如图1所示，根据实际工况，设计要求的基本参数包括：最大转动扭矩40kn·m，输送能力20m3/h，根据文献1，采用实体右旋单头螺旋，螺旋有效输送距离7.7m，卸料口525×525㎜。

图1 螺旋输送机结构示意图

1.1 螺旋直径及螺距

若已知输送机的生产率及被输送物料的特性，则可按下式计算螺旋的直径D（m）：

Q——输送机的生产率（t/h），设计为80t/h；

y——物料的充填系数，由文献表10-31（324页）选取为0.25；

b0——倾斜向上输送时对输送量的影响系数，水平取为1；

k2——螺旋螺距P与直径D之比例系数，螺距P的大小与螺旋直径及输送机的布置、物料的特性有关。该螺旋水平布置，输送的物料流动性好，具有一定的磨磋性，取为0.7；

r——被输送物料的堆积密度（kg/m3），氧化铝为4.0×103kg/m3；

n——螺旋转速（r/min），根据经验取为44.5 r/min；

g——重力加速度，g＝9.8m/s2;

计算得螺旋直径D=0.375m，圆整为400㎜。螺距P=0.9×400＝360㎜，取350mm。

1.2 螺旋转速

试验研究表明，当输送机的螺旋超过一定的转速时，输送物料颗粒便开始产生在垂直于输送方向（沿径向）的跳跃，输送能力降低，磨损增加，从而对输送过程产生不利的影响。螺旋转速太低，单位时间输送能力降低。但是，由于至今尚缺乏这方面的具体资料，因此在实际计算中，往往采用下列经验公式来确定螺旋的最大许用转速（r/min）：

A——经验系数，由表10-31得A=50。

计算得nmax=79.05r/min

1.3 螺旋轴直径

为了减轻自重，螺旋轴一般采用管轴，壁厚一般取为4～12㎜。管轴外径的大小与螺距有关，根据资料推荐的轴径计算公式：

1.4 充填系数的验算

根据文献有关公式可以计算出物料填充系数：

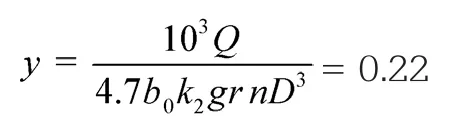
符合螺旋输送机设计有关要求。

综上，此螺旋输送机可确定其参数：D=400mm，n＝55r/min，d＝219mm。

2 基于PRO/Mechanica的螺旋体弯曲变形及模态分析

Pro/MECHANICA可以实现与Pro/ENGINEER的完全无缝集成，该软件可以直接利用Pro/ENGINEER生成的几何模型进行有限元分析。由于Pro/ENGINEER具有强大的参数化功能，那么在Pro/MECHANICA中就可以利用该优点进行模型的灵敏度分析和优化设计。具体说，当模型的一个或多个参数在一定范围内变化时，求解出满足一定设计指标（如质量最小、应力最小等）的最佳几何模型。因此，本文选用Pro/ENGINEER进行三维实体建模。

图2 加上约束及载荷的螺旋力学模型

图3 螺旋体有限元网格模型及网格划分信息

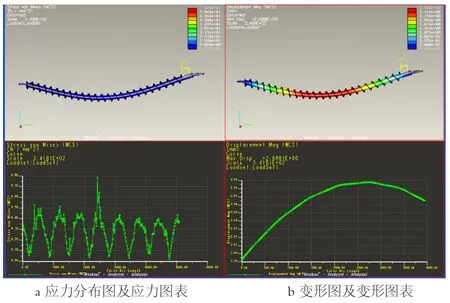
图4 螺旋体应力分布、变形图及图表（螺旋轴直径为219㎜）

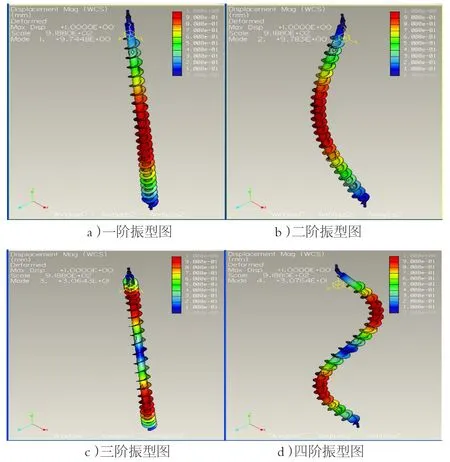
图5 螺旋体各阶振型图

根据经验公式计算得到的螺旋体的有关参数，虽有其合理性的一面，但与实际工况也存在着一定的差别。螺旋轴直径过粗，降低有效输送面积，过细则会降低其强度。本文将利用PRO/Mechanica有限元分析软件对螺旋体从整体上进行分析。

2.1 建立螺旋体力学模型

首先根据上述确定的参数进行分析。

在自重和物料的作用下，两支座（为简支梁）之间的螺旋将发生弯曲变形。螺旋主要承受扭矩M，切向力P切，法向力P法及螺旋本身自重的作用，即处于剪应力和压应力的作用下。P切和P法可通过电机传动功率求得，将P切和P法等效到y和z坐标轴上，加上约束，在Pro/E环境中建立如图所示的力学模型：

2.2 划分网格

在AutoGEM中选择实体选项，然后点击创建，即可对模型进行自动网格划分。螺旋体的有限元网格模型如图3所示。

2.3 螺旋体弯曲变形分析

按照设计要求，工作时螺旋最大弯曲挠度不得超过5㎜（螺旋外径与槽体内壁间距），图3为有限元计算得到的应力分布图、变形图及图表。结果表明螺旋体的最大变形量为2.688㎜，小于5㎜。

从上面的分析可知，设计参数存在一定的设计裕量，能满足强度、挠度设计要求。

2.4 螺旋体有限元模态分析

螺旋体在工作时处于旋转状态，如果其固有频率与其工作频率接近或相等时，会发生共振破坏，因此，设计时应该进行模态分析，避开各阶固有频率。

对螺旋体有限元模型的求解，一般不需要求出振动系统的全部固有频率和振型，由于低阶模态对振动系统的影响较大，因此本文仅计算前四阶模态。

螺旋体工作频率为0.9Hz，根据计算结果，该螺旋体的固有频率避开了正常工作频率，可知螺旋体的刚性较好。

3 结论

（1）本文通过传统的串行设计，确立关键参数，建立三维模型，对螺旋体进行有限元静、动力学分析，计算出螺旋体的应力及位移，并求出其前四阶固有频率和振型。通过应力、变形、振型和动画显示可以很直观地分析螺旋体的动静态性能，并且找到零件的薄弱环节，为螺旋体的结构设计提供理论依据。

（2）本文采用Pro/MECHANICA有限元分析软件对螺旋体进行分析，并通过它实现了实体建模和有限元分析计算的无缝集成，提高了有限元分析工作的效率。这为其他的零部件的结构设计提供了新的方法。