数形结合 避繁就简——借助函数的凸凹性巧解一类不等式的参数问题

☉云南省开远市第一中学 龚敬辉

导数综合题型中有一类含有一次式的不等式问题.其题型新颖，结构简单，但入口隐蔽，只有通过细心观察之后，才会发现这些题都披着一层伪装——切线，只要拨掉这层伪装就会变成熟悉的形式.整个过程蕴含着化归与转化的思维，再借助函数的凸凹性（数形结合的方法）就可轻松解决.

一、问题提出

题1（2017年全国卷Ⅲ理科21题）已知函数f（x）=x-1-alnx，若f（x）≥0，求a的值.

题2（2017年全国卷Ⅱ文科21题）设函数f（x）=（1-x2）·ex，当x≥0时，f（x）≤ax+1，求a的取值范围.

通过观察分析可以发现，这两道试题属于同一类型问题：变形后都会含有一个一次式的不等式的参数问题.其题型新颖，结构简单.如果用平时的常规方法解决，情况较多，运算量大，不易做对.但如果把问题进行转化，再借助函数图像的凸凹性形状特点与它的切线相对位置关系（数形结合的方法）就可轻松解决.本文就探讨一下这种题型的解题方法和规律.

下面先熟悉一下函数的凸凹性的有关知识.

二、预备知识

判定：设函数y=f（x）在区间（a，b）内有二阶导数f″（x），如果对所有点x∈（a，b），有f″（x）>0（<0），称函数y=f（x）的图像在区间（a，b）上为下凸（上凸）（如图1）.

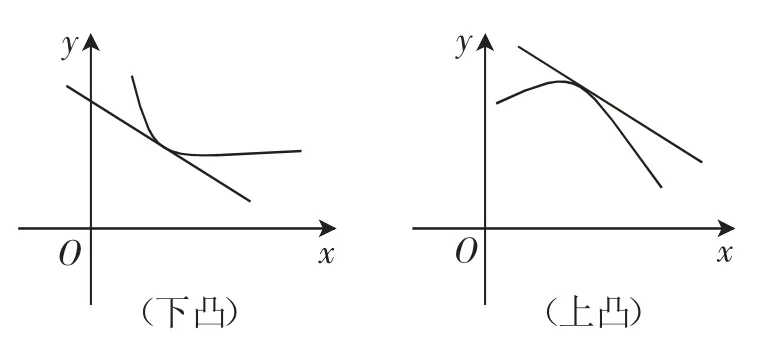
图1

性质：（1）如果函数y=f（x）的图像在区间（a，b）内下凸，则在区间（a，b）内任意一点的切线，都在曲线的下方（切点除外），即f（x）≥f′（x0）（x-x0）+f（x0）（x0∈（a，b））.

（2）如果函数y=f（x）的图像在区间（a，b）内上凸，则在区间（a，b）内任意一点的切线，都在曲线的上方（切点除外），即f（x）≤f′（x0）（x-x0）+f（x0）（x0∈（a，b））.

三、探究过程

题1的解答：问题转化为：当x＞0时，x-1≥alnx恰好成立.

令g（x）=x-1，h（x）=alnx.

通过观察发现（1，0）为g（x）=x-1与h（x）=alnx的公共点.

因此要想使，当x＞0时，x-1≥alnx恰好成立，g（x）=x-1必须是上凸函数h（x）=alnx（h″（x）＜0，a＞0）的切线，其中（1，0）为切点.

图2

即h（x）=alnx的图像在切线g（x）=x-1的下方（除切点）.

所以h′（1）=1，则a=1（如图2所示）.

题2的解答：先讨论若x≥0，f（x）≤ax+1恰好成立时的情况.

由于f（x）=（1-x2）·ex，所以f′（x）=ex·（1-2x-x2），f″（x）=ex·（-1-4x-x2）.

当x≥0时，f″（x）≤0，所以f（x）在［0，+∞）上为上凸函数.

通过观察发现f（x）=（1-x2）·ex与h（x）=ax+1的公共点为（0，1）.

因此要想使，当x≥0时，f（x）≤ax+1恰好成立，h（x）=ax+1必须是上凸函数f（x）=（1-x2）·ex的切线，其中（0，1）为切点.

f（x）=（1-x2）·ex在［0，+∞）上的图像在切线h（x）=ax+1的下方（除切点）.

所以a=f′（0）=1.

因此结合图形可知，当x≥0时，要想使f（x）≤ax+1恒成立，只需a≥1即可.（如图3所示）

图3

从以上可看出：借助函数的凸凹性与它的切线相对位置关系，特别通过变形后找到曲线函数与直线函数的公共点，以其为切点，问题就可解决.

下面我们来探讨在近几年各种考试中出现的这类型题的解题方法，总结规律.

例1（2016年全国卷Ⅱ文科20）已知函数f（x）=（x+1）lnx-a（x-1），若当x∈（1，+∞）时，f（x）＞0，求a的取值范围.

解析：问题化为：当x∈（1，+∞）时，不等式（x+1）·lnx＞a（x-1）恒成立.

令h（x）=（x+1）lnx，g（x）=a（x-1）.

曲线h（x）=（x+1）lnx与直线g（x）=a（x-1）有一个公共点P（1，0）.

要使（x+1）lnx＞a（x-1）在（1，+∞）上恰好成立，那么直线g（x）=a（x-1）必须是h（x）=（x+1）lnx在（1，0）处的切线.

所以a=h′（1）=2.

而当x∈（1，+∞）时，不等式（x+1）lnx＞a（x-1）恒成立，即x∈（1，+∞）时，h（x）的图像必须在直线g（x）的图像上方，此时a≤h′（1）=2（如图4）.

例2是否存在常数a，b使得x2≥ax+b≥2elnx对任意的正实数x恒成立？若存在，求出a，b的值；若不存在，请说明理由.

解析：通过分析可知，两曲线y=x2，y=2elnx有公共点

图4

易知曲线y=x2是下凸，曲线y=2elnx是上凸.

所以若存在常数a，b使得x2≥ax+b≥2elnx成立，那么直线y=ax+b是曲线y=x2，y=2elnx的公共切线，切点为.（如图5）

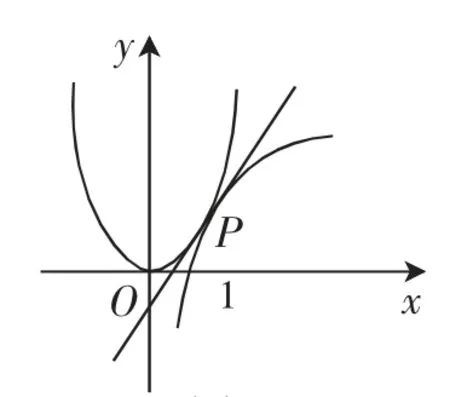
图5

由于（x2）′=2x，得直线y=ax+b的斜率为

四、拓展探究

最后我们再来研究一下与此相关的综合问题.

例3（2012年高考全国卷理科21改编）若ex-x≥ax+b对x∈R恒成立，求（a+1）b的最大值.

解析：令g（x）=ex-x，h（x）=ax+b，即g（x）≥h（x）.

由于g′（x）=ex-1，g″（x）=ex＞0，所以g（x）在R上是下凸函数.

要想使g（x）≥h（x）成立，则h（x）必须是g（x）的切线.

（转化的关键）如图6，设P（x0，y0）是函数g（x）图像上一点.

以P为切点的切线m：y-（ex0-x0）=（ex0-1）（x-x0），

所以a=ex0-1，b=（1-x0）ex0.

所以（a+1）b=（1-x0）e2x0.

设F（x）=（1-x）e2x，x∈R，则F′（x）=（1-2x）e2x.

图6

评析：本题的关键就是要从图形的角度去理解此不等式ex-x≥ax+b成立的意义——h（x）=ax+b是下凸函数g（x）=ex-x的切线，接下来一切就迎刃而解了.

五、规律总结

相信通过以上例题解析，大家已经掌握了解决此类问题的规律：（1）找出问题中的曲线与直线；（2）发现公共点；（3）曲线必须为下凸（上凸）形状，直线是以公共点为切点的切线.再结合曲线与切线之间的相对位置，就可以解决问题.

总之，从这些题目中可以看出，结构上只要是涉及含一次式的不等式恒成立问题，都可以考虑这种方法，利用几何图形的形状特点进行思考分析，当然使用该方法必须将图像形状（凸凹性）和位置分析得比较准确才行，特别是以公共点（切点）为突破口.那么问题就可转化为我们熟悉的形式，解决起来就有法可依，事半功倍了.