一堂异面直线距离的代数求法探究课
2019-10-11江苏省仪征中学张顺军
☉江苏省仪征中学 张顺军
求异面直线的距离一直是立体几何教学的一个难点.在以往的教学中,往往只注重立体几何本身的方法,而忽视了代数在解决此类问题中的作用,其结果必然导致学生思维狭窄,思路单一,无法把握“异面直线的距离”本质.为了解决这个问题,笔者上了一堂“异面直线距离的代数求法”探究课,摘录如下,供大家参考.
一、给出问题——探究几何通法
教师先提问学生:一个正方体的12条棱中有多少对异面直线,每对异面直线的距离是多少?然后给出下面例题,要求学生探究解法.
例1如图1,已知正方体ABCD-A1B1C1D1的棱长为1,求对角线A1B与B1D1两异面直线的距离.
本例极其普通,数见不鲜.从立体几何方法的角度去探究并不难.笔者要求学生分组探讨,5分钟后,他们找到了两种基本的解法.
思路1(平面射影距离法):设O、O1分别为面ABCD和面A1B1C1D1的中心,则A1B与B1D1两异面直线的距离等于B1D1与面A1OB的距离,也等于O1到面A1OB的距离,经过推证O1到面A1OB的距离为Rt△OA1O1的斜边上的高,然后求这条高.
思路2(利用转化思想):将两条异面直线的距离转化为两个平面之间的距离.因为A1B位于平面A1BD内,而B1D1位于平面CB1D1内,而这两个平面都与对角线AC1垂直,且把这条对角线三等分,不难计算,因而平面A1BD与平面CB1D1的距离为,这个距离也就是对角线A1B与B1D1两异面直线间的距离
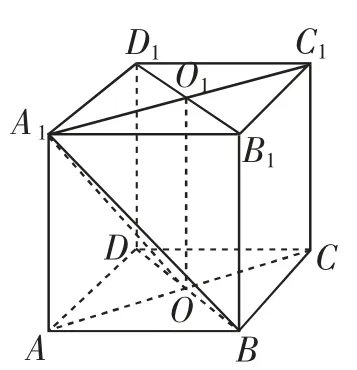
图1
二、变换图式——探究代数新法
数学所研究的往往是最本质的东西.笔者把例1的图形简化,便得到了下面的例2.
例2如图2所示,把一张由正方形ABCD和正方形ABEF组成的纸片折叠成一个直二面角,AB=1,你能求异面直线AC和BF的距离吗?
学生眼尖,一眼就看出这张图与图1的关系,于是建议补形,回到例1中不就解决了吗?笔者说,好马不吃回头草,能否想想用别的方法呢?方法总比困难多.学生思维顷刻陷入了困境,教室内鸦雀无声.于是,笔者出示例3:
例3如图3所示,接例2,P在线段BF上,PH⊥AC,垂足为这时线段PH的长能用x表示吗?能求出线段PH的长的最小值吗?
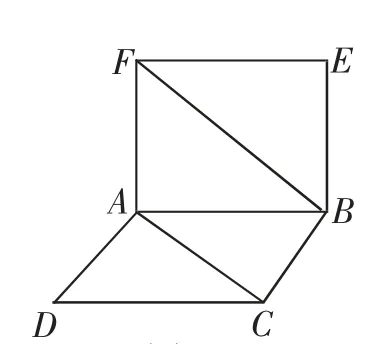
图2
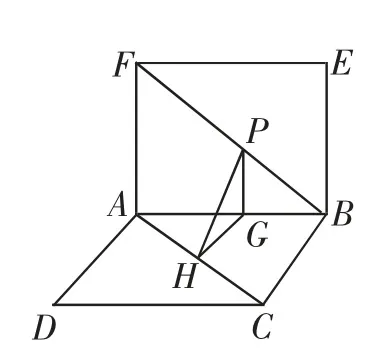
图3
由于给学生铺设了台阶,学生回答此例并不困难,他们先过P作PG⊥AB,垂足为G,并连接GH,并证明了△PGB,△GHA,△PGH都是直角三角形.于是在Rt△PGH中很快得出如下结论2),故
再利用二次函数的最值方法来求这个立体几何最值问题就不难了,他们很快得到,当时,PH的最小值为的最终结果.
笔者追问:为什么例2的计算结果与例1相同.难道例2计算的就是两条异面直线间的距离吗?学生会心一笑,他们参照两条异面直线距离的定义,参透了其中的奥秘和问题的本质,同时也感受到了几何问题代数化的神奇.
三、再变图式——辨别是非真假
学生解完了一类题,往往会造成一定的思维定式.为了及时消除这种思维定式,教师又提出了下列问题:
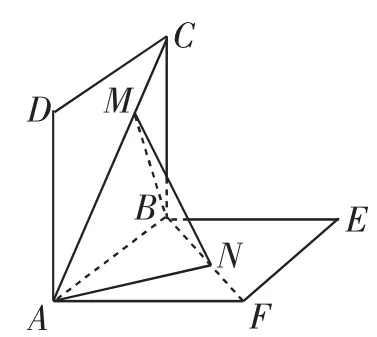
图4
例4如图4所示,接例3,M是线段AC上的动点,N是线段BF上的动点,且满足CM=,这时,你能用字母a来表示线段MN的长吗?如何求出它的最小值?这个最小值就是异面直线AC、BF之间的距离吗?
对于本例,笔者要求学生独立完成,不可交流.巡视时笔者发现学生有多种解法,由于受篇幅所限,这里只展示一种既简洁又明了的解法:
把原图视为由矩形CDEF(CD=1,DA=AF=CB=BE=1)沿AB把它折成直二面角(图5(1)),设MN交AB于P,根据题设有,折成直二面角后的平面角是∠MPN(图5(2)).
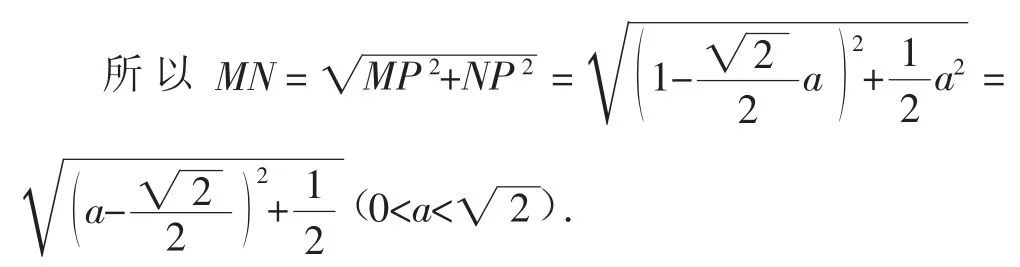
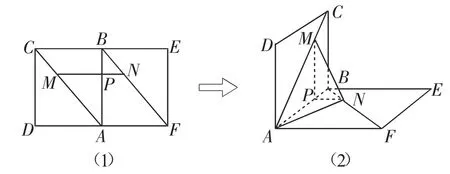
图5
那么,最小值就是异面直线AC、BF之间的距离吗?有些学生顺口而出:是的,但转念一想不对,上面两个例子算出的结果是,而这里是,怎么会出现两个数值呢?于是他们恍然大悟,本例中的两点M、N虽然也是动点,但他们互相制约,因而不是异面直线间的距离,那究竟该如何证明它不是异面直线的公垂线呢?这时非要动用反证法不可了.
接下来笔者引导学生用反证法加以证明,并提醒学生解题时一定要“具体问题具体分析”.
四、学生改题——尽显个人才华
教师:刚才我们从例1出发引出了一串问题,探究了两条异面直线距离的解法,那么,你能围绕“两条异面直线距离”这个主题,把例4改编成新的题目吗?允许互相探讨.
数分钟后,请两位学生上讲台交流.
生1:把条件“点M是线段AC上的动点”与“CM=BN=a(0<”分别改成“AM=CM”与”(如图6).
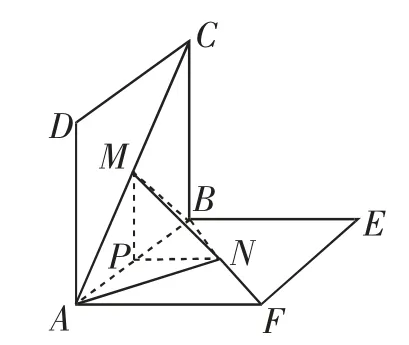
图6
要求的结论不变,还是用x的表达式f(x)表示线段MN的长度,并求出它的最小值,并考察这个最小值是否是异面直线AC、BF之间的距离.
解:(1)在平面ABCD内作MP⊥AB,垂足为P,连接PN,由题意不难得出MP⊥平面ABEF,所以MP⊥PN.因为M是AC的中点,所以
在△PBN中,∠PBN=45°,由余弦定理得:
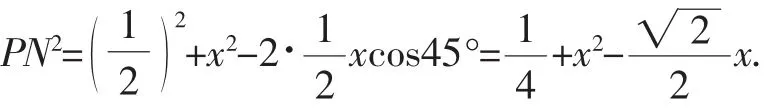
容易推出,MN与AC并不垂直,因而这个最小值不是异面直线AC、BF之间的距离.
我把要求解答的问题变为“用x,y表示线段MN的长度,并求其最小值,判断这个最小值否是异面直线AC、BF之间的距离.”
解:(1)在平面ABCD内作MP⊥AB,垂足为P,连接PN,不难得出MP⊥平面ABEF,故有MP⊥PN.由于CM=x,所以,所以
在△PBN中,∠PBN=45°,由余弦定理得:
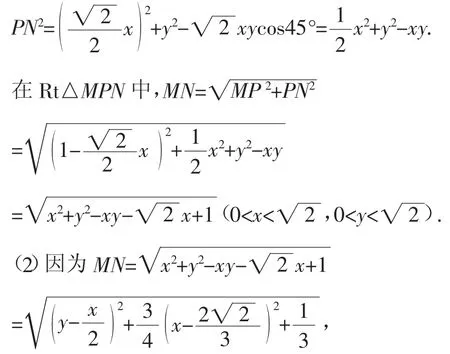
由于M,N相互独立,且M∈AC,N∈BF,所以MN的这个最小值就是异面直线AC、BF之间的距离.
教师点评:两位同学改题都很成功,解答也十分完整.两种不同改法,得到两个不同的结论,让大家再次看清了两条异面直线距离的“真面目”,同时也再次感受到了代数知识与几何知识“联合作战”的威力,请大家为这两位同学的精彩发言鼓掌(学生鼓掌雷动).
至此,学生对两条异面直线距离的代数求法有了一个清晰的认识,同时也对“异面直线的距离”这个概念有了更深层次的理解.
