解析构造函数在高中数学解题中的应用

☉山东省青岛第二中学 孙云涛

构造函数对学生的综合能力要求较高，不仅要牢固掌握并深入理解基础知识，而且需要具备灵活应用所学知识的能力.教学实践发现，多数学生不知道如何构造函数，面对数学试题要么走不少弯路，要么不知如何下手，因此，教师应围绕教学内容，讲解构造函数在不同试题中的应用，传授构造函数的解题技巧.

一、构造函数在不等式中的应用

不等式是高中数学的重要知识点，其较为抽象，相关题型复杂多变，部分试题采用常规思路便可求解，部分试题则需要学生构造函数，故难度较大.为使学生掌握不等式试题的解题技巧，教师一方面要做好不等式的基础知识的讲解，尤其在应用基本不等式求解时，应引导学生找到等号成立的条件，切实夯实基础.另一方面，在教学实践中应多积累优秀试题，引导学生深入分析不等式试题，传授构造函数在解题中的应用方法，帮助学生迅速找到解题的关键点.

例1设f（x）是定义在R上的奇函数，在（-∞，0）上有2xf′（2x）+f（2x）＜0，且f（-2）=0，则不等式xf（2x）＜0的解集为______.

该题目题干简洁，较为抽象，显然运用常规解法无从下手，此时应考虑采用构造函数法来求解.认真观察题干中给出的不等式，满足“xf′（x）+nf（x）”的形式，教师可引导学生尝试着构造函数F（x）=xf（2x），而后借助函数的奇偶性、单调性，以及数形结合等知识来解答.构造函数时，应注意题干中“f（-2）=0”这一条件的应用.

由题干可知，构造函数F（x）=xf（2x），则F′（x）=2xf′（2x）+f（2x），当x＜0时，F′（x）=2xf′（2x）+f（2x）＜0，即在（-∞，0）上F（x）单调递减.因为f（x）为奇函数，而y=x也为奇函数，由奇偶函数的知识可知F（x）是偶函数.显然在（0，+∞）上F（x）单调递增.因为f（-2）=0，则F（-1）=0，由上可大致画出函数图像，由图像易知其解集为（-1，0）∪（0，1）.故填答案为（-1，0）∪（0，1）.

二、构造函数在数列中的应用

数列是高中数学的重点与难点内容，包括等差数列、等比数列等知识点.数列可与其他数学知识综合命题，难度较大.在教学实践中，教师一方面要为学生深入讲解等差、等比数列的概念、通项公式的求解方法，使学生牢固记忆与灵活应用数列的相关性质；另一方面，优选具有代表性的试题，引导学生应用构造函数的方法进行求解，体会构造函数在解答数列试题中的应用过程，总结构造函数在解答数列试题中的技巧.

例2已知{an}为等比数列，且满足a1=2，a8=4，函数f（x）=x（x-a1）（x-a2）…（x-a8），则f′（0）的值为（ ）.

A.26B.29C.212D.215

该题目是数列与函数的综合题，难度中等，关键在于能够找到解题的突破口.认真分析给出的函数表达式及所要求解的内容，可考虑采用构造函数法，即构造函数f（x）=xg（x），而后应用数列性质进行求解.

令g（x）=（x-a1）（x-a2）…（x-a8），则f（x）=xg（x），对其进行求导得f′（x）=g（x）+xg′（x）.显然f′（0）=g（0）=a1·a2·…·a8，又因为a1=2，a8=4，则g（0）=a1·a2·…·a8=（2×4）4=212.故正确答案为C.

三、构造函数在解析几何中的应用

解析几何是高中数学的难点，是高考的必考知识，试题难度或难或易.解题中只有结合题干条件，灵活应用多种解法，才能提高解题效率，因此，在教学实践中，教师一方面应灵活应用多种教学方法，以帮助学生记忆与理解解析几何中的计算公式，如可以引导学生通过绘制思维导图，直观记忆各个知识点，构建系统的解析几何知识网络体系；另一方面，为学生创设新颖的试题情境，鼓励并引导学生应用构造函数法进行求解，帮助学生树立解题自信，不断提高有关解析几何试题的解题水平.

例3已知实数a、b、c、d满足，其中e为自然对数的底数，那么（a-c）2+（b-d）2的最小值为（ ）.

A.8 B.10 C.12 D.18

很多学生面对该题不知如何下手，只有极少部分学生能看出“（a-c）2+（b-d）2”表示的是两点间距离的平方，但究竟该如何解答仍是一头雾水.在教学实践中，教师应引导学生认真观察题目中给出的等式，然后进行化简并构造函数，便不难求解.

四、构造函数在三角函数中的应用

三角函数是高中数学的基础知识，围绕三角函数既可以单独命题，也可以与向量、函数结合起来命题.若和其他知识点结合起来命题，则难度一般较大，因此，在教学实践中，教师应注重解题方法的传授.一方面，三角函数与定义域密切相关，解答相关试题时，教师应引导学生在给定的定义域内分析问题；另一方面，围绕具体例题，为学生讲解应用构造函数解答三角函数试题的方法，使学生掌握这一重要的解题方法.

例4已知在时，不等式f（x）tanx＜f′（x）恒成立，则下列不等式错误的是（ ）.

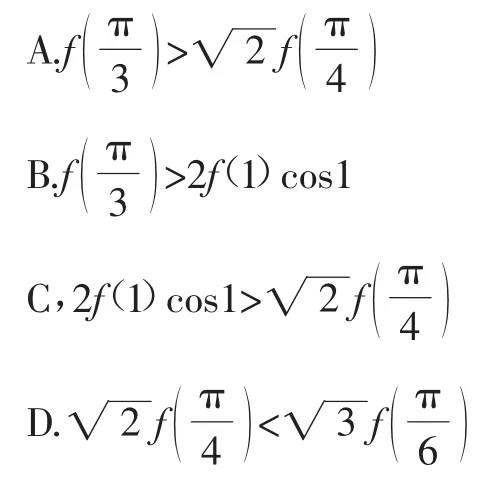
该题目以三角函数为背景进行命题，难度较大.认真分析题目中给出的不等式关系及定义域可知，当x∈时，sinx＞0，cosx＞0，结合所给的选项，可考虑通过构造函数F（x）=f（x）cosx来进行求解.

构造函数F（x）=f（x）cosx，则F′（x）=-f（x）sinx+f′（x）cosx.因为对任意的，不等式f（x）tanx＜f′（x）恒成立，即f（x）sinx＜f′（x）cosx恒成立，f′（x）cosxf（x）sinx＞0恒成立，即F′（x）＞0，故F（x）在上单调递增.易知，由此可知，所以，结合四个选项可知，只有D选项是错误的.故答案选D.

五、结论

构造函数是一种重要的解题方法，其能帮助学生迅速找到解题思路，并快速解题.但构造函数的专业性较强，很多学生不易掌握，因此，在教学实践中，教师应做好构造函数的教学研究.本文通过研究可得出以下结论：

（1）构造函数解题主要根据函数的单调性、奇偶性、周期性等知识点来进行求解，因此，在教学实践中，教师应做好函数基础知识的教学，使学生牢固掌握高中阶段各种函数的基础知识，为学生能够灵活构造各类函数奠定基础.

（2）为使学生加深对构造函数的认识，教师应围绕高中数学教学内容，讲解相关的例题.同时，优选经典题目，并不断地进行专题训练，鼓励学生总结与积累构造函数的技巧，提高学生构造函数的应用水平，促进其解题能力的进一步提升.