走近参数范围，探析方法视角

☉江苏省扬中高级中学 耿 燕

讨论参数的取值范围是近几年高考的热点问题，也是高中数学需要学生掌握的核心内容，考虑到该类问题的题型多变，所涉及的知识点较多，题型结构较为复杂，学生在实际求解时很难准确把握其中的切入点，从而造成突破困难，下面对其方法视角加以探析.

一、分离视角——分离参数，化归最值

在求解一些含有参数的不等式问题时，可以基于分离视角采用参数分离的方法，使不等式问题中的变量和参数分别置于不等号的两侧，从而将问题化归为不等式的最值问题，通过求解其值域或最值来实现对原问题的求解.即对于a≥f（x）恒成立问题，只需要求解f（x）max即可；而对于a≤f（x）恒成立问题，只需要求出f（x）min即可.

例1已知函数f（x），若对于任意的x∈［2，+∞）都有f（x）＞0，试求参数a的取值范围.

分析：题干中给出了函数f（x）的解析式，求当f（x）＞0时参数a的取值范围，实际上构建的是不等式问题，其中不等式中含有两个变量，即a和x，并对x的范围进行了设定，求另一变量a的取值范围，可以采用参数分离的方法，分别将a和x置于不等号的两侧，通过求最值来确定参数的取值范围.

解：根据题意可知，对于在x∈［2，+∞）上恒成立，进一步变形有a＞-x2+3x在x∈［2，+∞）上恒成立.可设h（x）=-x2+3x，则只需求出h（x）的最大值即可，即，则当x=2时，h（x）取得最大值，且最大值为2，则a＞h（x）max=2.所以参数a的取值范围为（2，+∞）.

评析与总结：参数分离后的一侧应为函数原式，需要对其取值范围加以讨论，进而确定其最值，而求解函数的最值也是一个难点，必要时可以引入导函数，通过求导的方式来加以确定.另外，还需要掌握一些不等式问题中常见的变量分离情形，例如：①f（x）≥h（k）恒成立⇒f（x）min≥h（k）；②f（x）＞h（k）恒成立⇒h（k）＜f（x）min.

二、构造视角——构造函数，借用性质

在求解不等式、方程等参数范围问题时，利用分离参数有时会存在一定的困难，而且无法分离出独立的函数，此时就可以考虑采用构造函数的方法，在不等式问题中构造出新的函数，利用函数分析的方式来讨论参数的取值范围.

例2若不等式对于任何大于1的自然数n均成立，试求参数a的取值范围.

分析：题干中给出了对应的不等式，且表明不等式成立的情形，求其中参数a的取值范围，考虑到不等式较为特殊，可以考虑在其中构造对应的函数，研究函数的单调性，通过求新函数的取值来确定参数a的取值范围.

解：设f（n）=2），分析可知f（n+1）-f（n）＞0，则函数f（n）是关于n（n∈N，n≥2）的单调递增函数因此要确保不等式始终成立，只需要保证即可，从而可解得，即参数a的取值范围为.

评析与总结：在上述求不等式中参数的取值范围时，所采用的是构造函数的方法，并基于函数的性质来分析参数的取值范围.而研究函数的取值范围需要考虑两点：一是函数的定义域，二是函数的单调性.前者是函数取值合理性的保证，后者则是利用函数变化规律来推导取值的关键.

三、数形视角——分离函数，图像分析

相对而言，不等式参数求值问题较为抽象，计算过程较为烦琐，如果不能准确分析不等式的特征，则很容易造成解题停滞，而数形结合是解决该类问题较为有效的策略.利用数形结合方法来求解不等式参数问题时，可以基于题干中的不等式分离出相应的函数，然后绘制出相应的函数图像，通过几何意义转化及图像分析的方式来直观求解.

例3已知不等式关于x∈［-4，0］恒成立，试求参数a的取值范围.

分析：题干中给出了不等式恒成立的情形，并求解相应参数的取值范围，由于不等式涉及根号，若采用参数分离的方式则计算过程较为烦琐，因此可以考虑采用数形结合的方式，以不等号为分割点，分别在两侧构建相应的函数，则问题转化为比较两函数值域的大小问题，然后分别绘制出两函数的图像，通过分析图像的特征来求参数的取值范围.

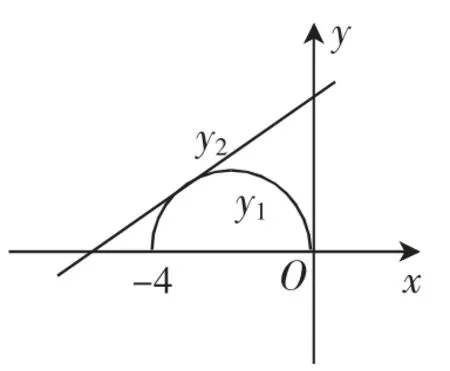
图1

解：分别设，对函数y1进行变形，可得（x+2）2+y12=4（y1≥0），则其图像是以（-2，0）为圆心，2为半径的上半圆，而函数y2为单调递增的直线.将两图像绘制在同一直角坐标系中，如图1所示，若要使不等式成立，则需要满足y1＜y2在区间x∈［-4，0］上恒成立，其几何意义就为在对应区间上函数y1的图像均位于y2的下方.结合图像分析可知，只要圆心（-2，0）到直线的距离大于2，且1-a＞0即可，即d=，解得a＜-5，所以参数a的取值范围为（-∞，-5）.

评析与总结：数形结合求解参数取值实际上利用了不等式的几何意义，同时也体现了函数、方程、不等式之间的紧密联系.在进行不等式变形构建函数的过程中，除了需要考虑两者自变量的有效性，还需要掌握一定的技巧，如一般分离函数时需要确保其中之一为已知的简单函数，这样才更容易讨论参数的取值范围.

四、变换视角——主元变换，提炼构式

在求解不等式问题中的参数取值时，一般其中含有两个变量，在解题时我们习惯上将其中的x视为主元，而将另一变量a视为参数，如若按照常规的思路进行变形分析，则过程较为烦琐复杂，因此可以考虑采用变换主元的策略，将参数a视为主元，而将x视为要求取值范围的参数.

例4若实数p满足|p|≤2，试求不等式x2+px+1＞2x+p恒成立时x的取值范围.

分析：在上述不等式中出现了两个变量x和p，解题时需要将其中的一个变量视为主元，将另一个变量视为是已知的常数.如若将x视为主元，但由于其取值未知，而p的取值范围在题目中已经进行了限定，则用常规方法求解则存在一定的困难，因此可以考虑将p视为主元，则问题转化为分析定义域［-2，2］上关于p的函数恒成立问题.

解：对不等式进行变形，则有（x-1）p+x2-2x+1＞0.设f（p）=（x-1）p+x2-2x+1，则需要使f（p）在［-2，2］上始终大于0，分析可知函数f（p）为单调函数，则需要满足从而可解得综上可知，x＜-1或x＞3.所以x的取值范围为（-∞，-1）∪（3，+∞）.

评析与总结：从上述的变换主元可知，主元变换前后并不会改变不等式的性质，只是问题分析过程中一种思维变换的方法.同时该种方法同样是建立在函数思想之上的，需要充分利用函数性质和图像特征等知识.一般适用变换主元法求解参数取值的问题具有以下特点：一是含有两个及两个以上的变量，二是其中一个变量具有明确的取值范围.

总之，虽然参数取值范围问题受题干不等式、题设条件、构建方式的影响题型较为多样，但实际上其求解方法也较为固定，上述所探究的只是其中几种常见的解题视角和方法，在实际解题时需要全方位、多视角地对问题进行审视，从而灵活地选取方法，以求高效求解.而在实际教学中需要教师多加引导并拓展学生的解题思维，提升学生的解题能力.