基于马尔科夫链的三峡枢纽船型结构预测

卢文昌，张培林

（武汉理工大学 交通学院，湖北 武汉 430063）

1 引言

三峡枢纽是连接长江上游和中游的关键节点，极大地促进了长江上游和中游的航运发展，对黄金水道起到至关重要的作用。但随着货运需求的不断增长，船舶过闸供需矛盾日益突出[1]。三峡船闸设施设备已连续多年处于高负荷运行状态，已进入检修高峰期，船舶待闸成为常态。自2011 年首超设计能力以来，三峡船闸停航检修次数持续增多，待闸时间也不断增加。2017 年南线船闸停航33 天检修，三峡南线船闸单线运行通过能力仅为正常时期的40%，此期间船舶只能通过水深较浅的三江航道，船舶平均待闸时间由2011 年的17h 增加到106h，每天待闸成本超过千万。预计十四五期“645工程”建设完工，宜昌-武汉段航道水深提升至4.5m，万吨级船舶将全年通航。过闸船舶进一步大型化，5 000吨级以上船舶约占41%，平均吨位达4 337t，2010-2017年年均大型化率约11%，给船闸工作人员增加了工作负担和难度。未来船闸通航船舶如何发展，是解决三峡枢纽运输瓶颈问题必须考虑的重要因素。

关于三峡枢纽的船型结构目前没有人研究过，但从结构演化角度看，一般使用马尔科夫链模型和解释结构模型来研究。裴彧[2]为了弥补灰色马尔科夫预测模型自身的不足，首次将新陈代谢模型与残差优化的灰色马尔科夫模型结合，从而达到修正灰色模型的目的，并应用到桥梁健康状态的预测当中。朱会霞[3]等采用马尔科夫模型和区间自适应遗传算法建模，进而预测出东北三省产业结构。潘杰[4]等采用滑动无偏灰色GM（1，1）和马尔科夫链建模，对灰色模型的残差相对值用马尔科夫链进行修正，进而预测出2017 年西安地铁二号线客流量。刘宗明[5]等采用灰色GM（1，1）和马尔科夫链模型建模，对灰色模型的残差绝对值序列用马尔科夫链模型进行调整，最终得出太原市漪汾桥断面的交通量。马彩雯[6]等采用灰色GM（1,1）和马尔科夫链模型建模，利用积分思想对灰色模型背景值进行优化，修正灰色模型残差，从而预测出2016 年我国铁路客流量。刘晓琴[7]等采用马尔科夫链模型和统计估计法建模，预测出2007 年北京西站铁路春运客流量。彭舰[8]等提出了基于马尔科夫链的轻轨乘客轨迹预测新算法，结合贝叶斯分类器、最近一次出行轨迹与常住地的关系，预测出下次出行轨迹。贾云蒲[9]根据单线地铁客流增长的规律与特征，采用灰色Verhulst模型预测西安市地铁2号线客流量，通过对原始数据进行对数变换，再利用马尔科夫模型进行修正，最终得到误差更小的预测结果。Antoni Wilinski[10]在函数值的字段中创建具有固定长度和固定划分为间隔的时间窗序列，优化目的在于找到最佳窗口长度、窗口数量和间隔数量，以提高转换矩阵的预测效率，一阶马尔可夫链和二阶马尔可夫模型的测试取得了良好的结果。Zhenxiang Xing,Han Zhang,Yi Ji,Gong Xinglong,et al[11]基于自适应Metropolis 算法（AM-MCMC）来解决CM中单个模型的权重，并获得权重的概率分布和所有权重的联合概率密度，最后获得最佳重量组合。Pangun Park[12]综合考虑感测链路、致动链路和恢复机制，通过马尔可夫链建模，对模拟结果进行评估。受上述成果的启发，本文通过数据采集处理，构建马尔科夫链模型，预测出2020、2030、2040 年和稳定年的三峡枢纽船型结构。

2 三峡枢纽过闸船舶结构分析

三峡枢纽过闸船舶多种多样，代表船型有3 000吨级油船、300TEU集装箱船、5 000吨级普通货船等，具体见表1。

表1 三峡枢纽过闸代表船型

按船舶类型、船舶吨级和船舶尺度三个方面对过闸船舶进行分析，主要如下：

（1）船舶类型结构。2008-2017年三峡船闸过闸船舶类型比例变化如图1 所示。船舶运力以单船为主，船队被淘汰的格局基本不变。目前客船占比虽年均递减7%，但随着普通客船和客货船的基本淘汰，旅游市场的开放及旅游客船的快速增长，未来客船占比将有上升的趋势；随着国家经济发展和产业结构的调整，危险品船、商品车船、多用途船和集装箱船的占比有上升态势，普通货船占比总体上有下降趋势；非运输船舶占比仍有持续减少趋势。

图1 2008-2017年三峡船闸过闸船舶类型比例图（单位：%）

（2）船舶吨级结构。2008-2017年三峡枢纽过闸船舶吨级结构如图2所示。过闸船舶以3 000t为界，3 000t以下的船舶持续下降，3 000t以上的船舶稳步上升。3 000t 以下的船舶由2008 年的90.8%减少到2017年的32.5%，年均递减率10.8%；3 000t及以上的船舶由2008 年的9.2%增加到2017 年的67.5%，上升了6.3 倍，年均递增24.6%。5 001t 及以上的船舶增长尤为显著，增长了约32倍，已成为目前占比最大的船型。

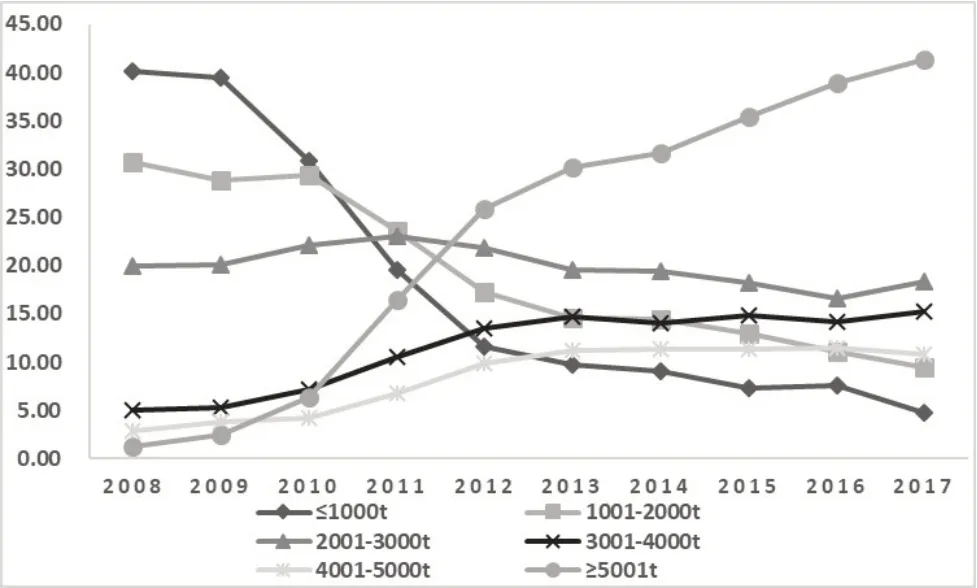
图2 2008-2017年三峡枢纽过闸船舶吨级结构（单位：%）

（3）船舶尺度结构。2014-2016年三峡枢纽过闸船舶尺度比例如图3 所示。2014-2016 年，三峡枢纽过闸船舶低于30m 长的比例由2.4%增加到6.0%，上升了1.5 倍，年均递增57.7%；30-50m 的比例由0.1%增加到1.7%，年均递增3.1 倍；50-90m 的比例由33.8%减少到33.34%，年均递减0.6%；90-180m 的比例由63.7%减少到58.9%，年均递减3.8%。

图3 2014-2016年三峡枢纽过闸船舶尺度结构（单位：%）

3 马尔科夫链模型

3.1 模型简介

马尔科夫链是一组具有马尔科夫性质的离散随机变量的集合。它描述了一种状态序列，序列中每个状态值只与前面的有限个状态有关，与其他因素无关；随机变量的所有可能取值，都在“状态空间”这个集合内。马尔科夫性质可用一个恒等式表示，即P（Xn+1=x|X1=x1，X2=x2，...，Xn=xn）=P（Xn+1=x|Xn=xn），这里x 为随机过程中的某个状态，也被称为“无记忆性”。

马尔科夫链中随机变量的状态随时间的变化被称为“演化”或“转移”。随机变量间的条件概率被称为“转移概率”，有单步转移概率和n步转移概率两种形式，分别如下：

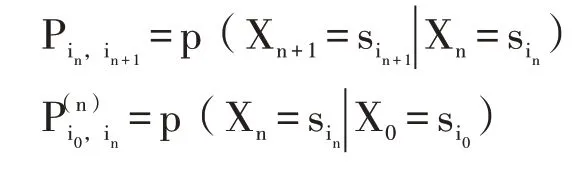
若一个马尔科夫链的状态空间是有限的，则可在单步演变中将所有转移概率按矩阵排列，得到转移矩阵：

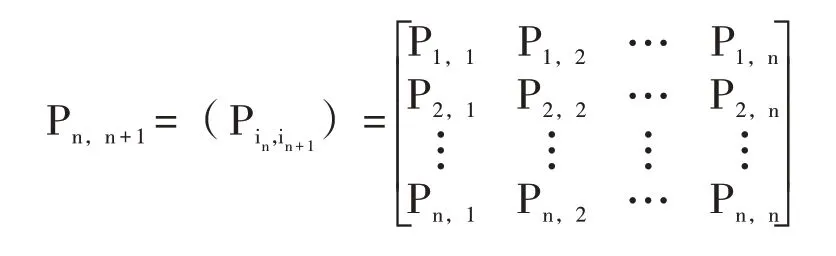
一些马氏链经过长时间的演变，会到达一种平稳的状态，称之为平稳分布，这种马氏链称为正则链，且正则链存在唯一的平稳分布。若状态空间内的某个概率分布π 满足π=πP，且0＜π（si）＜1,‖π‖ =1，则π 是该马氏链的平稳分布。式中P=（Pi，j）是转移矩阵和转移概率，该方程也被称为平衡方程。若某个概率分布π 满足π（si），则该分布是马氏链的极限分布。极限分布与初始分布无关，且一定是平稳分布，反之不成立。

3.2 模型构建

求解马氏链的关键在于求解转移概率矩阵，求解方法一般有统计估计法、线性方程组法、多元回归法等方法。统计估计法要求采集大量样本，样本数过少或不具备代表性都会影响模型精度，同时采集大量样本耗时耗力，估计状态转移概率也相当繁琐，统计误差较大。线性方程组法必须对每个方程进行显著性检验，若不显著，则必须采用其他方法计算，使计算过程更加繁琐。多元回归法需要考虑很多影响因素，计算量大且复杂。总之，这几种方法都存在着些许不足。

与上述研究方法不同，笔者利用简单有效的最小二乘法求解转移矩阵，以误差平方和最小为目标函数，转移概率的非负性和归一性为约束条件，建立非线性规划模型，如下：

利用n 步转移矩阵的性质即可预测出任意时刻的状态，即：

求出概率转移矩阵P0后，再用平衡方程即可求出平稳分布πk。

式中，δ 表示误差平方和，矩阵A 表示船舶结构样本数据，A 中的某一行表示某一年的船舶结构数据，aij表示船舶结构数据中第i 行的第j 种状态，P0表示单步转移矩阵，Pij表示第i 种状态向第j 种状态的单步转移概率，s.t.表示约束条件，πk表示船舶结构样本数据的平稳分布。

4 三峡枢纽船型结构预测

4.1 模型求解

将图1 中某一时刻三峡枢纽通航船舶的种类设为状态，则状态空间E1={客船，普通货船，集装箱船，危险品船，船队，非运输船}，它们之间的单步转移矩阵为Pi（6×6）。把2008-2017年的船舶类型比例数据代入式（1）-（3），得出单步转移矩阵P1、S2020（1）、S2030（1）、S2040（1）；根据正则链的判定条件，马氏链M1是正则链，故而存在唯一的平稳分布，代入式（4）计算出平稳分布π1，结果如下：

将图2 中某一时刻三峡枢纽过闸船舶吨级设为状态，则状态空间E2={1 000t 及以下，1 000-2 000t，2 000-3 000t，3 000-4 000t，4 000-5 000t，5 000t 及以上}，它们之间的单步转移矩阵为Pj（6×6）。把2008-2017 年的三峡枢纽船舶吨级比例数据代入式（1）-（3），得出概率转移矩阵P2、S2020（2）、S2030（2）、S2040（2）；同样的，马氏链M2也是正则链，代入式（4）计算出平稳分布π2，结果如下：

汇总以上结果，见表2。

表2 三峡枢纽船型结构预测（单位：%）

4.2 模型检验

以2008 年的三峡枢纽船舶结构作为基准，对2009-2017年的船舶结构预测数据进行矫正，不断优化概率转移矩阵，直至误差达到最小值，误差统计见表3。由表3可知，每年误差平方和总体呈下降趋势，偶有反弹，类型结构和吨级结构总误差分别约为1%和2%，模型精度已相当高，完全满足使用要求。

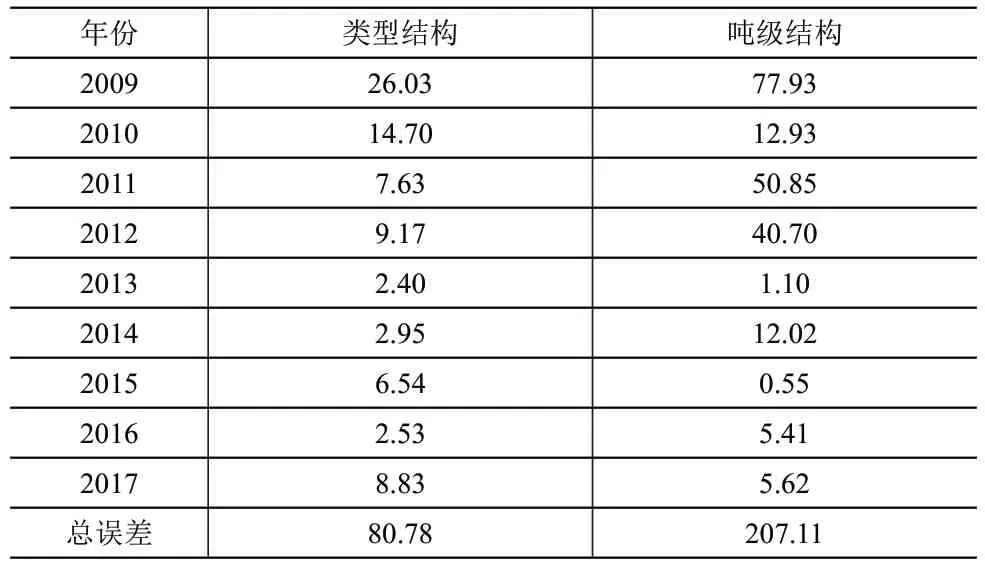
表3 2009-2017年三峡枢纽船舶结构预测误差统计（单位：‱）

4.3 结果分析

三峡船闸过闸船舶从类型上看，主要是普通货船、集装箱船和危险品船，客船和非运输船仍保持较低的份额，船队运输基本销声匿迹。平稳分布π1表明普通货船、集装箱船和危险品船的比例分别是54.8%、17.3%和21.9%，合计94%，符合现有船舶的专业化趋势。由于旅游市场的逐步开放和普通货船、客货船的淘汰，旅游客船将占有一席之地，最终稳定在4.2%。非运输船比例逐年下降，由于航道整治工程和公务船的存在不会完全消失，最终稳定在1.5%。船队比例持续下降，最终完全消失。

过闸船舶从吨级上看，主要是5 000t 以上，尤其是10 000t 以上。随着“645 工程”的建设完工，万吨级船舶通航成为常态，船舶大型化趋势显著。平稳分布π2表明2 000-3 000t、3 000-4 000t 和5 000t 以上的船舶比例分别是13.1%、11.5%和63.0%，合计87.6%。1 000-2 000t 和4 000-5 000t 船舶比例持续下降，最终保持稳定，原因是重庆及以上河段受到水深限制，仍继续使用这些吨位的船舶，无法持续加大或减小吨级。1 000t以下船舶已退出市场，原因是该船舶经济性差，逐渐被大吨位船舶替代。

过闸船舶从尺度上看，主要是50m以上，尤其是90m以上，预计50m以下的船舶均会被淘汰。总之，未来过闸船舶主要是普通货船、集装箱船和危险品船，首先是10 000t 以上、船长90m 以上，其次是5 000-10 000t、船长50-90m。

尤其需要指出的是，任何模型都有其适用条件和适用领域，马尔科夫链模型也不例外。马尔科夫链仅研究某个时间序列的数据变化趋势，没有考虑其影响因素，建模有待进一步优化。同样地，用于建模的样本也在很大程度上决定了模型性能。本文以2008-2017 年的三峡枢纽船舶结构样本数据作为计算基础，样本数量和代表性方面不一定是最优的，还需进一步寻优。采用非线性规划模型求解转移矩阵是一种行之有效的方法，但不一定是最优算法，遗传算法、神经网络、模式搜索等智能算法的预测结果可能更优。

5 结论

综合以上分析，得出如下研究结论：

（1）本文构建基于马尔科夫链的三峡枢纽船型结构预测模型，由该模型预计2020 年、2030 年和2040 年的长江三峡枢纽船舶类型结构（客船：普通货船：集装箱船：危险品船：船队：非运输船）和吨级结构（1 000t 及以下：1 000-2 000t：2 000-3 000t：3 000-4 000t：4 000-5 000t：5 000t 及以上），最终保持稳定，分别为4.2:54.8:17.3:21.9:0.3:1.5和0:3.3:13.1:11.5:9.0:63.0。经过模型检验，本文预测结果具有较高的可信度，为研究解决长江三峡枢纽船舶拥堵和未来发展提供一定的参考价值。同时，与现有研究方法相比，具有计算简单的优点。

（2）研究发现三峡枢纽未来过闸船舶主要是普通货船、集装箱船和危险品船，首先是10 000t 以上、船长90m以上，其次是5 000-10 000t、船长50-90m。客船和非运输船仍保持较低的份额，船队运输基本销声匿迹。船舶吨级日益增大，年均增长率约11%，1 000t以下船舶退出市场。那么，长江三峡船舶结构是否一定存在稳定值？在何种条件下出现稳定值？本文得到的结果是否巧合？有待进一步探讨。