基于单向频繁模式树的频繁项集挖掘算法
2019-10-11蒋东洁李玲娟
蒋东洁,李玲娟
(南京邮电大学 计算机学院,江苏 南京 210023)
0 引 言
关联规则挖掘[1-2]是数据挖掘中一个非常重要的研究领域,其要解决的问题是快速找到满足最小支持度的频繁项集。频繁项集挖掘方法可以分为产生候选项集的方法和不产生候选项集的方法。前一种方法以Apriori[3]算法为代表,该算法需要多次扫描数据库,并生成大量候选集,效率较低;后一种方法以FP-Growth[4-5]算法为代表,不需要产生候选项集,只需扫描两次数据库,节省了大量的I/O时间,因此总的效率有很大提高。
FP-Growth算法在挖掘过程中要创建复杂的数据结构,绝大部分时间主要消耗在构造和遍历FP-tree及条件FP-tree上。如果能够提高这方面的效率,将有助于提高算法的总体效率。FP-Growth*[6-7]算法在创建条件FP-tree时创建一个二维数组,使用该数组存储FP-tree中任意二个项目的出现次数,减少了FP-tree的遍历时间;文献[8]对FP-tree的构造过程进行改进,同时用hash结构存储频繁项头表,有效减少了项搜索时间;文献[9]提出了一种不用构造条件FP-tree,直接利用最初FP-tree生成的被约束子树进行挖掘的算法,因为该算法不用递归地构建条件FP-tree,可以节省大量的存储空间,同时该算法缩减了每一个节点的域的个数,只保留指向父节点的指针,与FP-Growth算法相比,所需的存储空间减少了一倍,效率提高了一倍。
文中在文献[9]算法(称其为改进前算法)的基础上,将被约束子树分为指向相同端点和不同端点这两种情况进行挖掘,设计了一种新的基于单向频繁模式树的频繁项集挖掘算法(unidirectional frequent itemset mining,UFIM)。
1 有关定义
设I={i1,i2,…,im}为m个不同项目(Item)的集合,D={T1,T2,…,Tn}为包含n条事务记录所构成的事务数据库,Ti(i=1,2,…,n)是其中一条记录,由I中若干项组成。设X为由项组成的一个集合,若X∈T,则称记录T包含X。
定义1 支持度[10-11](support):规则X→Y在数据库D中的支持度是D中同时包含项集X和Y的概率,记为sup(X→Y),即
sup(X→Y)=P{X∪Y}=|X∪Y|/|D|
定义2 置信度[10-11](confidence):规则X→Y在D中的置信度是指在包含项集X的条件下包含项集Y的概率,记为conf(X→Y),即
conf(X→Y)=P{Y|X}=sup(X→Y)/sup(X)
支持度和置信度这两个阈值是描述关联规则的两个重要概念,支持度反映关联规则在数据库中的重要性,置信度衡量关联规则的可信程度。给定一个数据集D,挖掘关联规则问题就是产生支持度和置信度分别等于或大于用户给定的最小支持度(minsup)和最小置信度(minconf)的关联规则。
定义3 单向FP-tree(UFP-tree):UFP-tree是一种树结构,该树[12-13]由一个标号为NULL的根节点(root)、一个项前缀子树(item prefix subtress)集合、一个频繁项头表(frequent-item header table)构成。
项前缀子树中的每个节点由4个域组成:item-order,count,node-ahead,node-next。其中:item-order指该节点所代表的项的序号,count指通过该节点的事务个数,node-ahead指向最左子女节点或父节点,node-next指向右兄弟节点或节点链中下一个节点。
频繁项头表中每个表项由3个域组成:item-order,count,node-next头。node-next头指向UFP-tree中具有相同item-order的第一个节点。
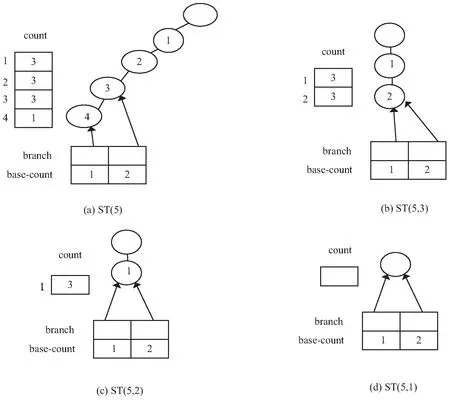
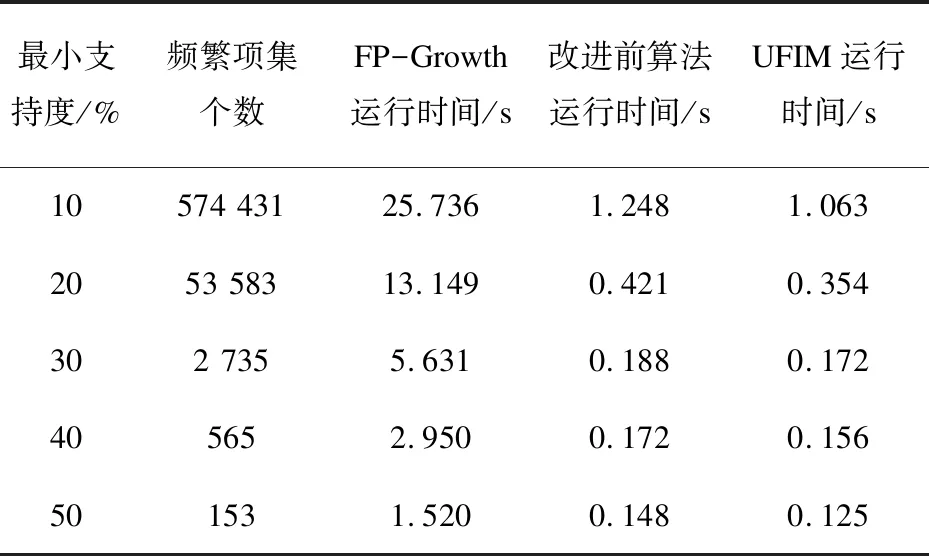
定义4 被约束子树[14]:设ki<… (1)UFIM算法总体思想。 UFIM算法采用分而治之的思想[15],通过扫描两次事务数据库,将事务数据库中的数据放在一棵高度压缩的数据结构UFP-tree中,使其可以在内存中存放,并且可以将重复的事务压缩为一条事务。然后对该数据结构进行迭代,通过模式增长的方式挖掘出所有频繁项集。 (2)UFIM算法流程。 UFIM算法包含两个阶段:UFP-tree构造阶段和UFP-tree挖掘阶段。 UFP-tree构造阶段: ①扫描事务数据库,得到频繁1-项集,并对其降序排序,生成项-序转换表和序-项转换表。 ②创建UFP-tree的根节点,对数据库中每个事务,首先将事务中的频繁项转换成对应的序号,并降序排序,然后再将排序后的每个item-order递归插入到UFP-tree中,最后先根遍历UFP-tree,将ahead指针翻转。 UFP-tree挖掘阶段: 对UFP-tree进行挖掘时,采用自底向上的递归思想,首先根据头节点列表中的元素所指向的节点生成被约束子树,然后针对这棵被约束子树端点相同和端点不同两种情况分别以组合方式和递归方式挖掘出包含该元素的所有的频繁项集。对头节点列表中的所有元素均自底向上执行该操作,最终挖掘出所有的频繁项集。 UFIM算法的流程如图1所示。 基于定义3,UFP-tree用如下过程UFPTreeC()来创建。 图1 UFIM算法流程 过程UFPTreeC() 输入:事务数据库D,最小支持度计数min-count 输出:单向FP-tree 步骤: ①扫描事务数据库D,得到每个项的支持度计数,删除支持度计数小于min-count的项 ②将项按支持度计数降序排序,得到每个项的序号,并生成项-序转换表和序-项转换表 ③创建UFP-tree的根节点 For数据库中每个事务t do { UFP-tree中的current指针初始化,指向根节点T; 删除itemset中支持度计数小于min-count的项,将剩下的项转换为序号,并降序排序得到orderlist; } For orderlist中每一项item-order do { UFP-tree_insert(item-order); } ④按先根遍历整棵UFP-tree,把每个节点c及其父节点p作为一个队列元素放入队列Q中; ⑤ For 队列Q中每一个元素q do { q.c.node-ahead=q.p;//翻转父节点指针 将节点c插入到项头表的c.item-order的项节点链中,作为该节点链中最后一个节点; } 其中函数UFP-tree_insert()的伪代码如下: 函数UFP-tree_insert(item-order) { if current指针所指向的节点没有子女节点 then 创建一个值为item-order的UFP-tree节点node,current.node-ahead=node; 修改current指针,使其指向新节点node; Else if current指针指向节点的子女节点中有值为item-order的节点 then 该子女节点的count值增加1,并修改current指针指向它; Else 创建一个值为item-order的UFP-tree节点的node; 将节点node插入到比node.item-order大的第一个节点之前,并使其count值为1; 修改current指针,使其指向新节点node; } 以表1中前两列数据构成的事务数据库D为例,若最小支持度计数min-count为3,则频繁1-项集为f,c,a,b,m,p,它们的支持度计数分别4,4,3,3,3,3;它们的序号分别为1,2,3,4,5,6,从而得到表1第3列的有序集。 表1 示例数据 根据以上给出的UFP-tree的详细构建过程,基于表1生成的UFP-tree如图2所示。 图2 基于表1数据生成的UFP-tree ST(ki,…,k2,k1)是单向FP-tree的一条包含根的特殊子树。可以用三个数组表示:指针数组branch[],指向每条被约束子路径的端点;整型数组base-count,记录每个被约束子路径的基本频度计数;整型数组count[],记录被约束子树中具有相同序号的节点的频度计数和。 对于序号k,从k的节点链中的每个节点出发,自底向上搜索单向FP-tree,就可以构造ST(k)。 在UFP-tree构建完成后,就可以利用被约束子树递归地挖掘出所有的频繁项集。改进前算法给出了基于被约束子树的挖掘方法,在此基础上,文中将被约束子树分为指向相同端点和不同端点这两种情况,并对指针数组branch[]均指向同一端点的特殊的被约束子树的频繁项集挖掘方法进行改进。假设此时指向的端点是j,检查数组count[j]是否满足最小支持度计数。若满足,则此被约束子树的频繁项集为除根节点外的节点的排列组合;若不满足,则说明此被约束子树没有频繁项集。用此方法挖掘出的频繁项集与递归挖掘产生的频繁项集相同,但可在一定程度上减少递归次数和存储空间。 文中提出的UFIM算法的频繁项集挖掘部分主要包括UFPmining过程和mine过程。UFPmining方法的主要功能是产生频繁1-项集和生成包含一个约束项的被约束子树,然后调用mine过程产生长度大于1的频繁项集。算法具体描述如下: 过程UFPmining():在UFP-tree上挖掘频繁集 输入:构建好的UFP-tree和设定的最小支持度计数min-count 输出:所有的频繁项集及支持度 procedure UFPmining(UFP-tree) { Fequent_len =0; //频繁项集长度 fori=max-order downto 1 do { 将序号i对应的项放入频繁项集数组FP[]中; 输出序号i所对应的项和支持度count[i]/allTrans; 依据UFP-tree构造被约束子树ST(i) if(ST(i)有非根节点) mine(ST(i)); Fequent_len --; } } 过程mine()可以用迭代算法实现,为简洁起见,下面给出它的递归算法 procedure mine(ST(k1,…,km)) { //指向相同端点的特殊被约束子树 if(ST(k1,…,km)端点相同并且端点计数≥最小计数) 被约束子树的元素排列组合记为list; 输出FP[]∪list的每个组合,每个组合的支持度相同且为端点的支持度count[j]/allTrans; //j为端点 Else if(ST(k1,…,km)端点相同并且端点计数<最小计数) return;//没有频繁项集 //被约束子树指向不同端点 Else { fori=km-1 downto 1 do { if(count[i]>=最小计数) { 将序号i对应的项放入频繁项集数组FP[]中; 输出FP[]和支持度count[i]/allTrans; 依据ST(k1,…,km)构造被约束子树ST(k1,…,km,i) if (ST(k1,…,km,i)中有非根节点) mine(ST(k1,…,km,i)); Fequent_len --; } } } } 以对ST(5)的挖掘为例,其过程如下: 首先将序号5对应的项m放入数组FP中,输出频繁项集{m:0.6}(冒号后面是支持度),构造ST(5),如图3(a)所示,因为其有非根节点,所以要以ST(5)为参数调用mine()。ST(5)端点不指向同一节点,要采用递归的方式求频繁项集。i的初值是4,count[4] 图3 挖掘ST(5)过程中形成的被约束子树 在改进前的算法中,没有对端点相同的情况进行优化,其在挖掘ST(5)过程中还要构建并挖掘ST(5,3,2)、ST(5,3,1)、ST(5,3,2,1)、ST(5,2,1)。可见,文中的此项改进是有效的。 为了测试UFIM算法的性能,与FP-Growth算法及改进前算法进行对比实验。 算法运行环境:CPU为Intel(R)Core(TM)i5- 6200U 2.30 GHz,内存为8G,操作系统为Windows 10。算法实现用的编程语言为Java,编程环境为eclipse。实验数据采用mushroom数据集[15],该数据集含有119项,8 124个事务,平均每个事务有23个项。 (1)相同事务数、不同支持度下运行时间对比。 表2列出了相同事务数、不同支持度下各算法的运行时间。可以看出,在mushroom数据集中,UFIM的运行时间均小于改进前算法的运行时间。随着支持度减小,UFIM算法和改进前算法在运行时间上的优势越来越明显。这是因为,随着支持度减小,特殊被约束子树数量增多,UFIM算法可以快速生成频繁项集,避免了递归构建被约束子树和对其挖掘的时间。 表2 运行时间随支持度变化 (2)相同支持度、不同事务数下运行时间对比。 表3列出了在支持度为10%、事务数分别为1千至5千条记录的情况下,各算法的运行时间。可以看出,UFIM在不同大小的数据集上的运行时间都小于改进前算法的运行时间。 表3 运行时间随事务数变化 FP-growth算法比Apriori算法效率高几个数量级,但它需要产生大量条件FP-tree,极大影响算法效率。文中设计了一种基于单向FP-tree的频繁项集挖掘算法UFIM,该算法在挖掘过程中采用了虚拟的树结构—被约束子树,并且将被约束子树分为指向相同端点和不同端点这两种情况进行挖掘,对指向相同端点的被约束子树的挖掘方法做了改进。在mushroom数据集上的实验结果表明,UFIM算法能有效减少被约束子树创建次数,提高挖掘效率。2 UFIM算法设计
2.1 UFIM算法总体思想与流程
2.2 UFP-tree的创建



2.3 被约束子树的创建
2.4 频繁项集的挖掘
3 实验与结果分析

4 结束语
