基于高斯过程回归的公交到站预测方法
2019-10-11李香云张卫钢吴娟娟
李香云,任 帅,张卫钢,吴娟娟,伍 菁
(长安大学 信息工程学院,陕西 西安 710064)
0 引 言
目前,在智能公共交通系统领域,国内外学者对公交车到站时间的精准预测做了大量研究,常用且高效的模型主要有以下几种:
第一种是基于历史数据的预测模型。文献[1-2]将要预测的路段分割成若干段,利用历史行驶数据分别计算各子路段的平均行驶时间,求得最终的预测时间;文献[3]在此基础上引入有限状态机完善模型;文献[4]创新地利用GPS数据和路段在空间和时空分布上的特点,根据历史路段平均到站总时间与当前车辆位置与速度,预测到达下站所需要的时间;文献[5]采用逆向查找法,将瞬时速度与历史平均速度进行融合,利用粒子滤波算法预测公交车到达下站的时间;文献[6]利用交通流的时间变化规律获取交通数据周期性和局部变化的特征,建立了时间序列模型,预测出公交车到站时间。这种模型的预测精度很大程度上取决于采集的历史数据的准确性。
第二种是基于人工神经网络的预测模型。文献[6-7]将行驶距离、时段等作为影响因素,使用神经网络算法进行预测;文献[8]结合调度经验,对神经网络算法进行优化,最终建立了智能调度模型;文献[9]建立了基于小波神经网络的预测模型,改进了神经网络易引起振荡效应的缺点,并采用粒子群算法进行优化,有效避免了其陷入局部最优。
第三种是基于动态的预测模型。文献[10]利用SVM从历史数据中预测的时间作为矩阵输入Kalman滤波器,利用“更新方程”将最新的观测值加入到预测向量中,有效地提高了预测精度。但由于公交车到站时间是具有长期和短期特性的时间序列数据,因此文献[11]利用具有长短记忆递归神经网络LSTM作为静态预测模型,然后利用Kalman滤波作为动态模型对预测结果进行调整。
上述研究都是对公交车到站时间的精准预测,但由于客流量、车本身性能、交通拥堵等因素的影响,增加了公交车到站时间的不确定性。面对各种突发情况,市民选择公交出行时,对公交到站时间的区间估计尤为关注,因此有必要对预测值的置信区间进行研究。高斯过程回归(Gaussian processes regression,GPR)是一种基于统计学习理论和贝叶斯理论的非参数[12]机器学习方法,文中探索性地建立了基于GPR的公交车到站时间预测模型(GPR bus arrival time prediction,GPR-BATP),在对公交车到站时间进行精准预测的同时,得到预测值的方差估计值,然后由预测值减去标准差作为下限,预测值加上标准差作为上限,来确定预测值95%置信区间,实现对到站时间概率意义上的预测。
1 高斯过程回归模型建立
1.1 高斯过程
高斯过程(Gaussian processes,GP)是一个正态的随机过程,其任意维有限变量的联合分布服从高斯分布。
对于任意有限个x,即x1,x2,…,xn∈N,其相对应的有限个随机变量(f(x1),f(x2),…,f(xn))T均服从式1所示的概率分布,那么F=(f(x1),f(x2),…,f(xn))T为GP,则可记作F~GP(m(·),k(·,·))。
(1)
其中,F为联合正态分布;m(·)=(m(x1),m(x2),…,m(xn))T表示均值向量,m(x)=E(x)表示均值函数;k(·,·)=(k(x,x'))n*n表示协方差矩阵。
1.2 GPR模型建立
将高斯过程应用于回归问题进行建模时,考虑到目标值y含有噪声[13],即定义为:
y=f(x)+ε
(2)
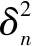
GPR的关键假设是所有输入的观测值Y以及预测值y*都服从联合正态分布,即给定训练集Train={(xi,yi)},i=1,2,…,n,Y=(y1,y2,…,yn)T服从的先验分布为:
(3)
其中,·=(x1,x2,…,xn)T;In为n×n阶单位矩阵。
如果给定测试集Test=(x*,y*),那么:
(4)
其中,k(·,·)为训练集X之间的n×n阶对称的正定协方差矩阵;K*=K(X,x*)为训练集输入X与测试集x*的n×1阶的协方差矩阵;K**=k(x*,x*)为测试点x*自身的协方差。
接下来,依据贝叶斯方法和联合正态分布理论,可求得预测值的后验分布为:
y*|X,Y,x*~N(μ(x*),var(x*))
(5)
其中
(6)
(7)
其中,μ(x*)为观测点x*的预测均值;var(x*)为对应的方差。
文中选择平方指数协方差函数(squared exponential covariance function,SE)(见式8)作为GPR的核函数。
(8)
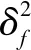
根据贝叶斯理论和最大后验概率估计原理,转化为求训练样本条件概率的对数似然函数L(θ),即:
L(θ)=log(p(Y|X,θ))=
(9)
上式对θ求偏导,可得:
(10)
则可得超参数集合θ。为了泛化,将均值设为0;γ=k(·,·)-1Y。
根据式10求得的偏导数,采用共轭梯度法或牛顿法(文献[14]中有详细论述)求得式9的最大似然函数和最优超参数θ。在进行预测时,根据得到的GPR模型,利用式6和式7式即可得到预测点的预测均值和方差估计值。
2 高斯过程回归的应用
2.1 数据描述
数据来源于2017年10月1日至10月24日天津市公交车的GPS记录。每条记录包含线路ID、车辆ID等。数据示例如表1所示。

表1 GPS数据示例
文中选择从10月9日至10月20日之间工作日的902线路公交车的26 377条GPS记录为训练集,选择10月24日的999条GPS记录作为测试集。仅对工作日进行讨论。
2.2 数据处理
2.2.1 轨迹数据预处理
GPS设备在采集数据过程中易受建筑物遮挡、设备故障等因素的影响,使得采集设备在部分时段缺乏位置信息,导致采集的数据存在丢失、异常等问题[15]。此时,若利用有异常的轨迹数据进行预测,会对预测的精度造成重大影响。为了降低噪声数据对预测模型性能的影响,首先使用阈值过滤法清洗数据;再判断数据是否存在缺失或异常;最后利用前后相邻轨迹点经纬度的平均值对缺失或异常数据进行修正。
2.2.2 数据整合
整合过程为:根据某条记录的下站编号与前一条记录的下站编号不同,与下一条记录的下站编号相同,判断此记录是否为停靠站,是则标记为1,否则,标记为0。然后根据某条记录的下站编号和是否为停靠站点来填充此条记录的下站站点的经纬度以及下站站点的时间戳。
整合之后,原始数据增加四列:是否为停靠站点、下站站点的经纬度以及下站站点的时间戳。
2.3 特征工程
2.3.1 路段距离
构造路段距离特征,计算方法为:
(11)
其中,lon1,lat1,lon2,lat2分别为当前记录和下一站站点的经纬度弧度数据;6 371表示地球半径(单位km)。
2.3.2 路段行程时间
根据整合后的数据,由当前时间戳和下一站站点的时间戳,求得当前位置到达下一站点的行程时间。
2.4 数据分析
以行车路段的距离、路口数两个影响因素为例进行讨论。
2.4.1 路段距离
将两个相邻的站点定义为一个行程区间,902线路的24个区间的各区间距离以及各区间行程时间如图1所示。
可以看出,行程区间距离的长短与行程时间的大小大致成正比关系,因此,根据行车距离预测行车时间具有实用价值。
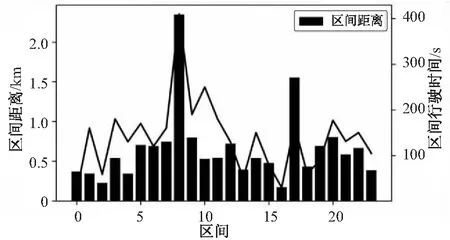
图1 区间距离与区间行驶时间对比
2.4.2 交通路口数
统计经过不同路口数时所需的行驶时间,如图2所示。
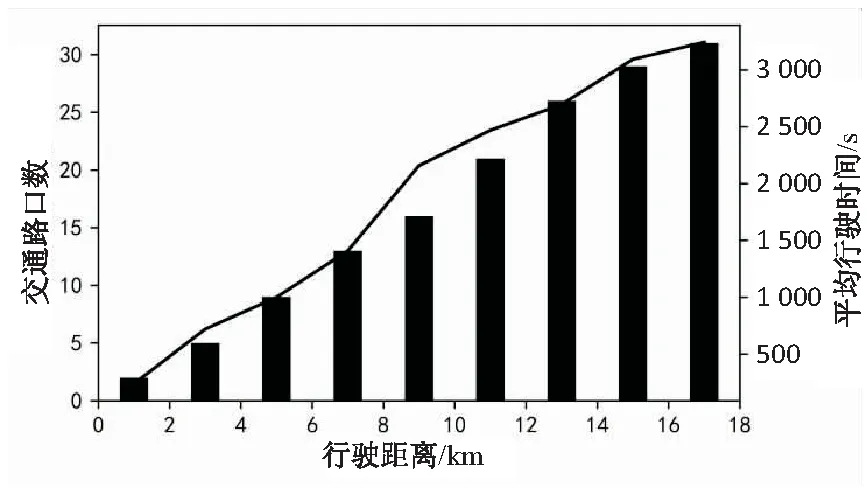
图2 不同距离不同交通路口数的行驶时间
结果显示公交车的平均行驶时间会随路口数及行驶距离的增加而增加。
2.5 GPR-BATP模型
GPR-BATP如下:
Yi+1=f(Xi)+ε
(12)
其中,Yi+1表示公交车到站时间的预测值;Xi表示与Yi+1相关的影响因子,f(·)为预测模型;ε为车本身性能、交通事故等未统计噪声。
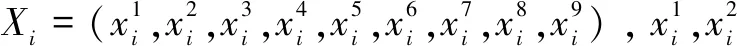
按照上述方法,通过原始数据集训练基于GPR的路段行程时间预测方法如下所述:
输入:原始数据集;
输出:GPR预测模型。
Step1:对原始数据集按照2.2和2.3小节的方法进行处理,得到训练集Train。
Step2:
Step2.2:基于训练集根据1.2小节的方法,按照式9、式10计算协方差函数的最佳超参数集合θ。
Step3:确定协方差函数k(x,x')。
Step4:得到GPR-BATP。
对于预测的数据集,处理方法同原始数据集,得到测试集Test。然后根据得到的GPR模型,对Test特征向量X进行预测。预测过程如下所述:
输入:待预测的数据集;
输出:公交车到达待预测站点的精准时刻T,预测值95%的置信区间[T-std,T+std],MAPE,RMSE,MAE。
Step1:对待预测的数据集按照2.2、2.3小节的方法进行处理,得到训练集Test。
Step2:
while:
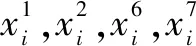
计算预测值μ(x*),var(x*)
end while
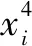
Step3:根据ypre和y计算得到MAPE,RMSE,MAE。
3 仿真实验
3.1 实验结果对比
分别采用GPR-BATP和SVM对902线路公交车24个运行区间的行程时间进行预测,结果如图3所示。
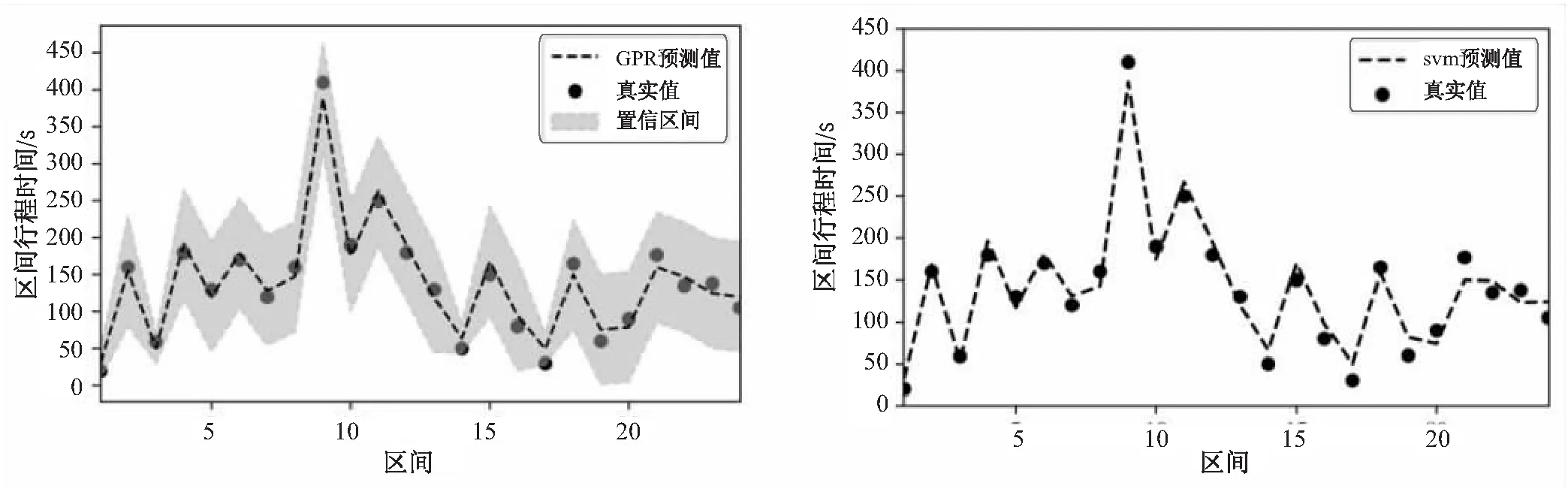
图3 GPR、SVM到站时间预测结果
3.2 预测方法性能对比
算法质量的衡量标准采用平均绝对百分比误差(mean absolute percentage error,MAPE)、标准误差(root mean square error,RMSE)、平均绝对误差(mean absolute error,MAE):
(13)
(14)
(15)
其中,m为数据样本集的样本数量;y_pre为预测值;y_true为真实值。
分别采用GPR和SVM公交车到站时间预测方法获得的预测性能指标如表2所示。
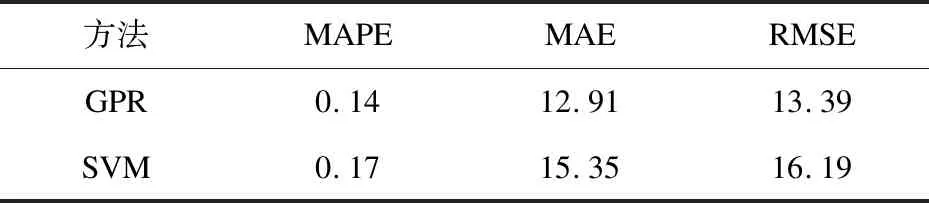
表2 两种方法的预测性能指标
可见,无论是MAPE、RMSE还是MAE,GPR模型可以获得与SVM相近的预测性能。相对于SVM,GPR-BATP具有如下优势[16]:
(1)最优超参数求取过程的系统化。SVM中参数求取只能通过交叉验证进行,而GPR预测模型利用贝叶斯理论通过最大后验似然估计方法来求取最优超参数集合。
(2)可以得到预测结果的误差带。在实现精准预测的同时,能够确定预测结果的置信区间,因此可以有效地对预测值的可信度进行把握。
4 结束语
文中提出一种基于GPR的公交车到站时间预测方法。实验结果表明,该方法不仅与SVM方法具有相近的预测精度,还能确定预测结果的95%置信区间,从而可以从概率意义上对到站时间实现准确预测,具有较高的实用价值和理论参考意义。
相对于SVM方法,该方法需要对实验数据进行归一化处理,这会影响实际预测过程的实时性。因此,如何提高GPR法的计算效率将是下一步的研究重点。另外,市民的出行规律(分为高峰期、平峰期、低峰期),也是影响到站时间的要素,也需要进一步研究。
