基于GRU-SVR的短时交通流量预测研究

潘伟靖，陈德旺

(1.福州大学 数学与计算机科学学院，福建 福州 350108;2.福州大学-星云股份智慧新能源研究中心，福建 福州 350108)

0 引 言

短时交通流量预测研究，为智能交通系统中的一个重要研究方向。该类研究可以为相关部门提供较为准确的城市道路流量信息，进而为相关部门对于路面车流的引导以及预警信息的发布提供相关决策依据，为市民的出行等提供了更为可靠的建议。因此，该类研究也具有一定的现实意义。

在短时交通流量预测的问题上，很多学者做了相关研究，如宫晓燕等使用的基于非参数回归的方法[1]以及张一基于卡尔曼滤波算法的研究[2]等一系列基于数学模型进行的研究。杨兆升等采用支持向量机[3]等机器学习方法进行预测。有部分学者采用一些混合模型，期望多种方法的互补，使得其模型的最终预测达到更好的效果，如采用SVM与卡尔曼滤波法相结合的研究[4]、将K-means与极限学习机相结合的方法[5]以及采用小波分析法与ARMA模型相结合的方法[6]等，在短时交通流量预测方向，取得了明显的进展。

随着深度学习及硬件设备等的蓬勃发展，不少学者尝试构建深层次神经网络，希望网络模型在预测结果精确度和可靠性上更高。其中对短时交通流量预测这类时间序列预测问题而言，最常用的便是RNN。

RNN是一种区别于传统前馈神经网络的新型网络，其设计思想是使神经网络具有一定的“记忆”功能，从而使训练后的RNN模型可以根据已有的若干个状态的值来对下一时刻S的值进行估测，正是因为这种“记忆”的特性，为时间序列预测、字符序列等问题提供了一个新的解决方案。但是，在训练标准RNN试图获取数据在一段较长时间内的特征时，RNN通常会出现梯度消失或梯度爆炸的情况[7]。于是有研究人员尝试将RNN的隐藏层基本单位由一个简单神经元节点改变为一个拥有记忆性的模块[8]。这种对标准RNN的更改中，最为著名的为Hochreiter和Schmidhu-ber提出的长短时记忆网络(long short term memory，LSTM)[9]以及Cho等提出的门循环单元(gated recurrent unit，GRU)[10]。这两种改进型的RNN，使得对一段相对较长时间内的特征捕获问题有了长足的进步。目前，RNN模型广泛应用在语音识别[11]、自然语言处理[12]、机器翻译[13]、语义分析[14]等方面。

有学者将LSTM运用于短时交通流量预测[15]，也有学者对LSTM与GRU两种模型在短时交通流量预测方面的性能做了比较[16]，也有学者将LSTM与SVR进行结合，得到了相对较好的结果[8]。由于GRU相对LSTM通常收敛较快[16]，计算量也就会相对减少。在结构上只包括更新门和重置门。其中更新门会对当前时刻保存传来的状态信息多少做出决策，重置门则正好相反，是对当前时刻丢弃或忽略传来的状态信息的多少做出判定。在LSTM与SVR相结合[8]的方法的启发下，文中提出一种将GRU与SVR相结合的模型用于短时交通流量预测，以期取得更高的预测精度和更快的运算速度。该模型使用门循环单元(GRU)对数据做特征提取，再将其输入到模型顶层的支持向量机回归(SVR)模型中以得到模型最终的预测输出。

1 模型设计

1.1 模型设计

提出的模型结构如图1所示。

图1 GRU-SVR模型框图

假设在模型训练时一次输入模型的数据长度为num，数据采样时间间隔设为Δt，即一次输入模型的一组数据之间的时间间隔为num*Δt，且训练集整体表示为D=(x1,x2,…,xn)，其中xi表示每个数据采样时间间隔内的交通流量数据。将训练集数据转化为向量V，表示为V=(V1,V2,…,Vm),其中Vi=(xi,x2,…,xi+num)。之后对Vi做切片，使得其前num个数据为模型的一次输入，最后一个为其对应的结果。在这之后进行汇总，形成真正的训练数据。对测试集数据也做相同的处理，得到测试数据。

将训练数据作为图1中的Input输入模型，训练GRU网络模型使之学习到相关参数。之后将数据集输入已训练好的GRU模型，获取到由GRU模型输出的特征向量，组成新的训练集与测试集。输入到SVR模型进行训练，得到最终的预测信息。相应流程如下：

Step1:对获取到的数据进行规范化处理；

Step2:以处理后的数据训练GRU网络模型，对输入数据进行学习；

Step3:将GRU网络输出的特征向量作为SVR模型的输入，并对SVR模型进行训练；

Step4:使用SVR模型进行预测，并将模型输出做反规范化得到预测结果。

1.2 具体设计

在GRU网络设计中，首先固定输入数据的长度进行设计。这里以num为12来进行设计。经反复迭代测试，在兼顾模型的计算量与最终性能的情况下，选择使模型在测试集上MAPE值达到最小的模型，并不断调整其余超参数，使得模型的平均绝对百分比误差(mean absolute percentage error，MAPE)以及平均绝对误差(mean absolute error，MAE)等指标逐步降低。GRU网络模型如图2所示。

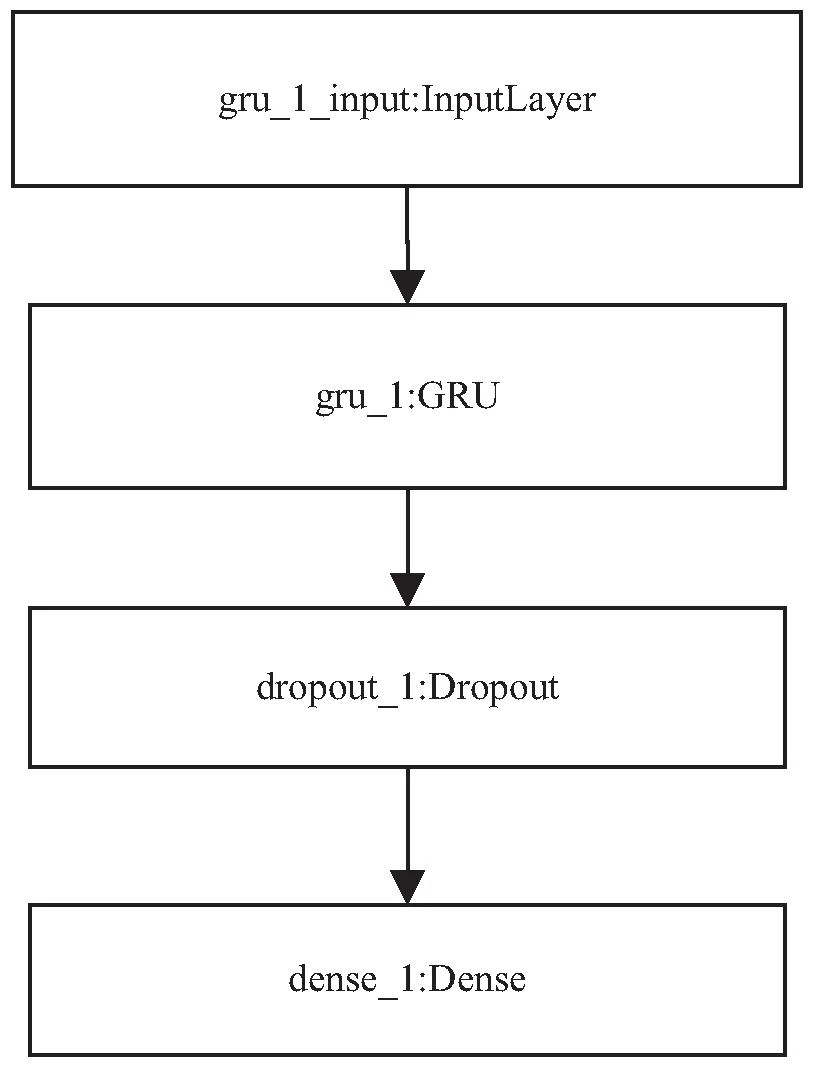
图2 GRU特征提取模型

在图2中，使用只有一层GRU网络层的网络结构，其中输入层单元数为12，隐含层的单元数为135，激活函数选择sigmoid，初始化函数选择he_uniform。之后，Dropout层随机断开50%的单元，再经过全连接层进行输出。Epochs为300。

在GRU网络结构确定之后，需要对SVR模型进行设计，在反复迭代测试之后，最终采用核函数为径向基(RBF)，惩罚因子C=1，gamma为0.3，epsilon为0.001的SVR模型。

2 实验数据及评价指标

2.1 实验数据

实验采用的数据来自加利福尼亚交通局公路绩效监控系统(Caltrans performance measurement system，PeMS)，使用的是加利福尼亚州萨克拉门托市I80-E检测到的采样间隔为5分钟的流量数据，时间为2018年4月到2018年7月，且使用的为工作日的总车流量。选择将4月的工作日数据作为训练集对模型进行训练，5月的工作日数据作为测试集。

2.2 评价指标

采取的评价标准为平均绝对误差(MAE)以及平均绝对百分比误差(MAPE):

(1)

(2)

3 实验结果及分析

3.1 实验分析

在确定网络模型及其所配置的使MAPE、MAE等评价标准最低的超参数后，设计采用不同的单次数据输入长度进行实验。实验的数据输入长度包括3，6，9，12。模型的预测结果如图3所示。

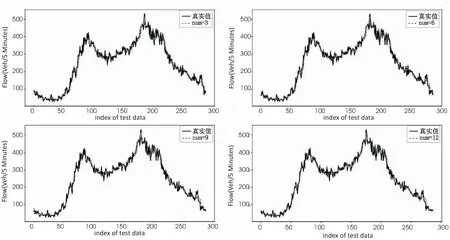
图3 不同num的模型对测试集数据的预测结果

使用上文所述指标进行评价，其结果如表1所示。

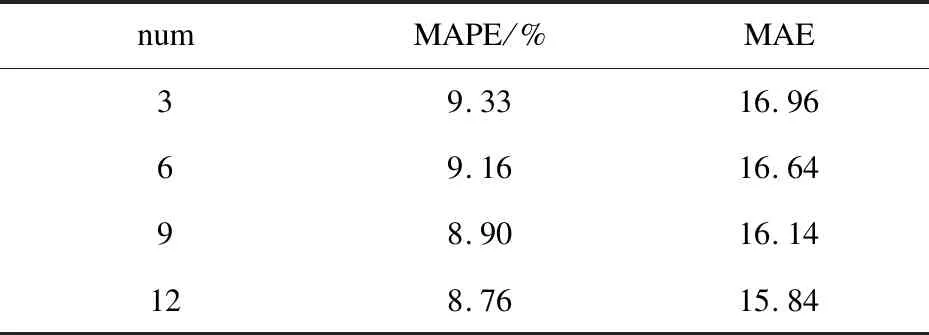
表1 不同数据输入长度模型的预测结果评价

如图3所示，在所有的实验中，单次数据输入长度为12的模型所预测出的曲线，与真实流量的曲线始终较为贴合，即误差始终在一个相对较小的范围内。同时，从表1中可以看到，在不同实验中，以num为12训练的模型，使得模型的预测误差值达到最低，在其之前的几个不同实验中，MAPE与MAE指标值均高于num为12的模型，但是都相差不大。所以仍然选择数据输入长度为12的模型进行预测，达到最佳的结果。

3.2 模型性能测试

为了测试该模型的泛化性，使用4月数据训练所得模型，分别对获取到的6、7月数据进行测试，其结果如表2所示。

表2 不同测试集上的性能比较

由表2可知，使用4月份数据作为训练集所训练得到的模型在6、7月份的数据集也有与5月份数据集上的相似表现，即使用6、7月数据作为测试集，其MAE、MAPE值与5月份数据作为测试集的对应评价指标浮动相对较小，说明该模型在非连续自然月的数据集上具有一定的泛化能力。

在这之后，对模型的抗噪能力也进行了测试。分别为5月份数据集加入三组具有不同均值、方差的高斯噪声以检测模型在不同情况下的抗噪能力。约定以“均值-标准差”的形式来表示每次测试的均值与标准差，其结果如表3所示。

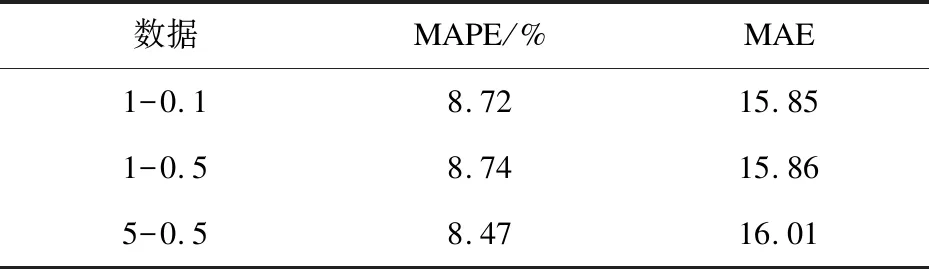
表3 加入不同高斯白噪声的性能比较

由表3可知，在加入高斯白噪声之后，模型的MAPE、MAE评价指标与原始测试集相比并没有产生过多的浮动。所以，可以说明该模型具有相对较好的抗噪性。

3.3 模型对比

为了验证该模型的性能，使用如上文所述的数据集进行训练及预测，即使用4月的数据进行训练，5月的数据进行预测，且分别与相同参数的GRU、SVR模型的性能进行对比，其具体结果如图4所示。

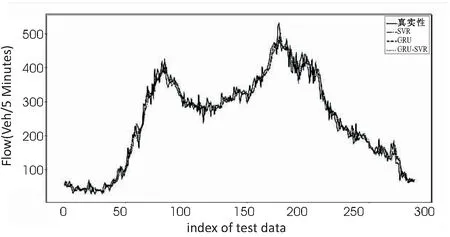
图4 不同模型的预测结果对比

其预测的误差如表4所示。

表4 不同模型的预测误差

由图4及表4可以看出，所有模型的预测曲线均可以较好地模拟出真实曲线数据，均较为贴合，相对误差均较小。但是，文中采用的模型相比于SVR、GRU，可以取得最低的MAPE以及MAE的值，说明该模型优于SVR和GRU模型，且GRU-SVR模型最终的r2值为0.97，是一种可靠的预测模型。

4 结束语

借助深度学习模型强大的特征提取能力以及支持向量机回归的预测能力，以结合门循环单元(GRU)与支持向量机回归(SVR)两种模型的混合模型对单一传感器的交通流量进行了相对较好的预测。但是，在大数据背景下，如何将机器学习与大数据相结合，仍是一个有前景的研究问题。对多个传感器在大数据背景下的短时交通流量预测问题，是下一步的研究内容。