基于辅助数据RetinaNet算法的销钉缺陷智能识别
2019-10-10王凯王健刘刚周文青何卓阳
王凯, 王健, 刘刚, 周文青, 何卓阳
(1. 华南理工大学 电力学院,广东 广州 510640;2. 广东省输变电工程有限公司,广东 广州 510160)
电力金具作为架空输电线路不可缺少的一部分,在电力系统中负责地线与杆塔、输电导线与绝缘子、杆塔与绝缘子等电力部件的连接,对系统的安全稳定运行起着重要作用[1-2]。然而由于多数电力金具除了要在环境恶劣的户外工作,还要长期承受外部机械负荷张力和电力系统内部的电力负荷的作用,使得金具上的销钉容易出现缺失或者松动等缺陷,影响电网的稳定运行。
近些年,为了提高对架空输电线路的巡检效率,无人机巡检技术得到了广泛的应用。针对电网设备的外在缺陷,无人机携带数据采集装置沿着线路走廊飞行获取大量可见光图片,人工寻找相应缺陷[3-4]。在此过程中,人工标注缺陷存在以下局限性:首先,在大数据环境下,即使是富有专业经验的人员进行标注,效率也是十分低下的;其次,销钉在图片中所占比例是十分微小的并且单张图片中可能存在多个销钉,致使人工标注经常出现漏检的情况;最后,由于无人机拍摄角度的原因,松动的销钉和正常情况下的销钉是十分相似的,这使得容易出现错标的情形。因此,针对该类缺陷,有必要研究一种准确而又高效的缺陷智能识别方法。
传统的电力元件以及缺陷识别方法主要集中于手工特征的设计,如借助图像增强、去噪等方法对图像预处理后,采用Harr特征、不变矩、彩色空间等特征并结合支持向量机、级联Adaboost等算法实现防振锤、绝缘子等电力元件以及相应缺陷的识别[5-7]。这类方法除了需要丰富的专业知识支撑外,往往只能针对某一特定类别起作用且可扩展性差。近几年,随着深度学习的迅速发展,有人提出了采用深度学习算法实现对电力部件以及相应的缺陷进行识别[8-10],然而这类研究多是集中于绝缘子、防振锤等元件的识别以及与之相关的绝缘子缺失、自爆等缺陷的识别,对于销钉级别缺陷的研究却是少之又少,甚至空白。另外,考虑到深度学习中的“单阶”检测算法RetinaNet在识别精度和实时性均要优于Faster R-CNN[11],本文提出一种基于RetinaNet的销钉缺陷智能识别方法;同时,考虑到销钉松动类样本的严重不足以及无人机收集该类样本代价高昂,本文采用人工采集的相关辅助数据对少数样本进行补充训练,并讨论了相关辅助数据量对闭口销松动类的平均准确率(average precision,AP)的影响,结果表明添加适宜的相关辅助数据量能够明显增加检测模型对少数类的重视程度。
1 用于销钉缺陷智能识别的RetinaNet算法
缺陷识别中最为棘手的问题是如何从大量的候选窗口中挑选出包含缺陷的候选区,迄今为止的目标识别算法可以分为两大类[12]:一类是以Faster R-CNN为代表的“双阶”检测器;另一类是所谓的“单阶”检测器,如YOLOv1、YOLOv2等。后者在实时性上优于前者,但是精度却没有“双阶”检测器那么高。为了提高“单阶”检测器的精度,以损失函数Focal Loss为核心、特征金字塔网络(feature pyramid network,FPN)为主要框架的RetinaNet检测器应运而生。
1.1 特征金字塔结构
RetinaNet检测器由主网络和2个具有特定功能的子网络复合而成。其中,主网络借助卷积神经网络计算输入图像的特征图,并且采用FPN结构将顶层特征和低层特征相融合,而与之相连接的2个子网络分别对FPN的输出进行分类和回归。在FPN出现之前的多数目标识别算法通常使用顶层特征进行预测,原因在于顶层特征蕴含丰富的语义信息,而低层特征的语义信息远没有高层的丰富。然而低层特征的高分辨率能够较为精确地反映待测目标的位置,因此FPN在不同的特征层采用融合后的特征进行独立地预测,其结构如图1所示[13]。
FPN综合考虑了低分辨率但语义信息丰富的高层特征和语义信息不足但分辨率高的低层特征,采用图1所示的结构使得各尺度下的特征都有丰富的语义信息。自下而上表示卷积神经网络的前向过程,在此过程中,部分层不会改变输入特征图的大小,于是将这些连续的不改变特征图大小的层视为一个阶段,每次抽取的特征正是每个阶段的最后输出,从而构成了特征金字塔结构;自顶向下的过程将分辨率较低的高层特征图进行2倍的上采样。上采样采用的是内插值方法,在像素点之间使用合适的插值算法插入新的元素,从而扩大特征图,确保上采样的特征图和下一层的特征图大小一致;随后对卷积神经网络前向过程生成的对应层的特征图进行1×1的卷积操作,将之与经过上采样的特征图融合,得到具有更加丰富信息的特征图。
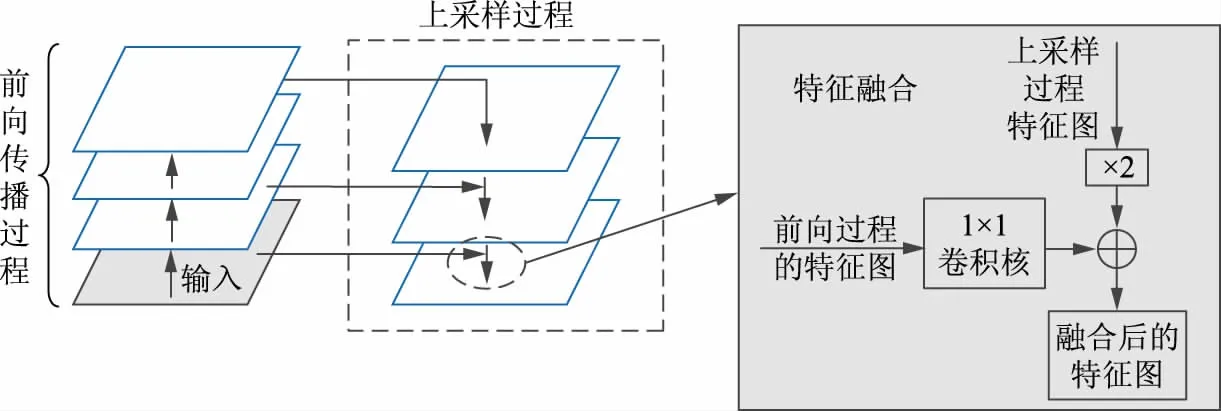
图1 特征金字塔网络架构 Fig.1 Feature pyramid network architecture
1.2 分类损失函数
“单阶”检测器的精度偏低归因于候选区域的类别不平衡,即图片中待识别目标通常只占整张图片的小部分,使得早期生成的候选窗口中绝大多数都属于负类(背景),只有极少部分包含前景物。背景类占优掩盖了包含识别对象的候选框的作用,使得训练过程无法充分学习到所需要的信息。对于Faster R-CNN,其包含的区域建议网络(region proposal network,RPN)事先对候选区域进行简单的二分类,从而属于背景的候选窗口将会大幅减少,这样在某种程度上降低了候选区域的类别不平衡所带来的影响,但其操作的复杂性却放慢了识别速度。
以二分类为例,常用的交叉熵损失函数
fCE(pt)=-log(pt).
(1)
其中pt定义为:
(2)
式中:p∈[0,1],表示模型将类别预测为y=1的概率;y为类别参变量。
为了能够从包含目标的候选区域学到更多的信息,文献[11]提出一种新的损失函数Focal Loss,在原有的交叉熵损失函数的基础上增加一个权重控制系数αt;另外,为了保证检测器能够有效区分难分样本和易分样本,增大难分样本的比重,在实际中,Focal Loss损失函数
fFL(pt)=-αt(1-pt)γlog(pt).
(3)
式中γ为调节因子。
2 销钉缺陷智能识别的难点分析及辅助数据集的构建
销钉作为电力金具不可或缺的部分,使得金具之间的连接更加稳固,销钉的松动甚至缺失往往会增加电力系统运行风险。图2给出了不同状态销钉的示例图。在外部因素(如环境因素)和内部因素(如负荷长期运行)综合作用下,有少数的正常状态下的销钉会蜕变为图2中所示的松动状态,甚至缺失状态。在没有了销钉保护的情况下,螺栓会进一步出现松动﹝如图2(b)所示﹞,这一连锁反应严重影响电力系统运行的可靠性。
2.1 无人机巡检数据的特征分析
电力系统绝大部分时间处于正常稳定运行状态,致使无人机巡检时采集到的绝大多数的数据样本都是正常样本,只有小部分样本存在缺陷;另外,销钉的松动以及缺失是外部机械张力和系统内部负荷长期作用的结果,短时间内很难获取到大量缺陷样本,从而进一步体现出销钉缺陷数据的稀缺性。实际情况中,无人机巡检采集到的数据正常样本偏多,销钉缺失类样本次之,而松动类数据量是非常少的。缺陷数据的不足使得各类别数据量失衡,而机器学习相关算法通常假定训练用的数据中各类包含样本数都是均衡的,训练数据本身的失衡导致训练出来的模型更加倾向于数据量居多的正常类,而“忽视”样本中数据量偏少的销钉松动类,这样训练出的模型在测试数据上的表现是欠佳的。

图2 无人机巡检采集到的销钉状态示例Fig.2 Examples of the status of pin collected by UAV inspection
另外,无人机本身的特性也增加了缺陷识别的难度:如无人机采集数据虽然具有较高的分辨率,但销钉在整张图片占据很小的比例[14-17];无人机航拍角度的随机性使得图片中的销钉形态发生变化;无人机本身飞行的不稳定性影响图片的清晰度等等。
2.2 辅助数据集的构建
针对销钉缺陷识别问题,提高缺陷类AP的意义远高于提高整体类的,然而缺陷数据较少出现、收集代价高昂给该类缺陷的识别带来了极大困难。倘若采用部分相关辅助数据样本弥补这一不足,对原有不平衡的数据集进行迁移学习,能够在某种程度上解决缺陷数据稀缺问题。但是,其他领域的数据与电力系统领域数据之间的差异较大,共享因素偏少,如果直接使用不相关辅助数据极易出现“负迁移”现象[18-19],并产生副作用。
针对销钉松动缺陷,参考架空输电线路实物模型的金具连接方式,在确保主要前景物(金具)一致的前提下,构建简易实物模型;随后将构建的实物模型放置在室外的任意环境中,人工模拟缺陷并采集相应缺陷样本;最后挑选出符合要求的数据构建辅助数据集,图3给出了部分试验用的相关辅助数据样本。由图3可知:前景物仅使用了瓷质绝缘子、玻璃绝缘子、U型挂环等金具,构造简单且易于实现;另外,由于可以实时模拟出销钉的各种状态,并且能保证背景的多样性,故完成了在短时间内获取大量销钉缺陷样本。

图3 人工采集的辅助数据样本Fig.3 Manually collected auxiliary data
3 缺陷智能识别的评价指标
对于一般的数据集,准确率、错误率等传统评价指标就能够对数据处理方法的性能进行衡量。然而,当面对数据不平衡的销钉缺陷识别问题时,以上评价指标可能会失效。在正常类别样本数占优的情况下,倘若将所有样本预测为正常类,这样准确率就会很高,显然训练出来的模型毫无用处。相关研究表明,查准率P与查全率R曲线(P-R曲线)可以明显地体现出不平衡数据的识别效果[20-21],针对每一类,都会有一条对应的P-R曲线,为此,本文采用对数据倾斜度十分敏感的P-R曲线作为评价指标,相关指标可根据表1数据进行定义。

表1 销钉缺陷识别的三类别混淆矩阵参变量Tab.1 Parameters of three-category confusion matrix for defect identification of pins
以松动类为例,查准率P和查全率R分别定义如下:
(4)
(5)
P-R曲线即是以R为横坐标、P为纵坐标绘制而成的曲线。对于每一条P-R曲线,其与坐标轴围成的面积即为该类别对应的AP。同时,采用AP的整体的平均准确率(mean average precision,MAP)对整体识别效果进行衡量。
4 实验与分析
实验在64位Windows操作系统上进行,所用的处理器型号为Intel(R)Xeon(R) CPU E5-2660 v4 @2.00GHz,运行内存为128 GB;显卡型号为NVIDIA Quadro M4000,显存为8GB;算法均在Keras框架中开展。
针对销钉缺陷识别问题,数据标签包括3类,分别为正常(标记为“normal”)、缺失(标记为“lost”)和松动(标记为“loose”)。实验用的数据可以划分为目标数据集和辅助数据集:前者是无人机现场巡检采集而得,具有较高的分辨率,并且单张图片可能包括多类标签,另外,待测目标在整张图片中占据很小的比例;辅助数据样本由人工采集而得。考虑到现实情况中销钉松动类样本较少出现、采集代价偏高,为了分析少数类辅助数据的量对测试结果的影响,本文分多次向训练集添加相同数量(137张)的松动类辅助数据。表2列出了实验用的数据分布状况,其中,测试集是从目标数据集中随机抽取而得,后续模型性能测试均采用这一测试集。

表2 销钉缺陷识别试验用的数据分布表Tab.2 Data distribution table for defect identification of pins
4.1 学习率对实验结果的影响以及分析
为了避免主网络初始化的权重给实验结果造成不确定性影响,FPN的主网络均采用在ImageNet预先训练过的ResNet-50,且采用随机梯度下降算法实现模型参数的更新。鉴于少数类(松动类)的正确识别的意义远超过数据占优的类别,通过观测少数类AP以及MAP完成销钉缺陷检测模型参数的优化。为了选取合适的学习率,本文以目标数据集为训练对象,采用学习率分别为1×10-2、1×10-3、1×10-4、1×10-5、1×10-6等5个不同的训练模型。其他参数设置如下:最大训练轮数为50,每一轮包含10 000次迭代,且αt=0.25、γ=2。图4为AP变化曲线。

图4 不同学习率下的AP与训练次数的关系曲线Fig.4 Relationship between AP and training times under different learning rates
根据图4可知,在销钉松动类数据样本严重缺乏的情况下,当学习率设置为合适的数值时,适当的训练次数不仅可以提高少数类的识别率,还可以有效提高总体AP。当学习率过高或者过低时,即设置为1×10-2、1×10-6时,模型在训练时越过局部最优值以及全局最优,使得测试精度趋于0;当学习率为1×10-4时,由图4可以直观地看到无论是少数类AP还是MAP,相对于学习率为1×10-3、1×10-5来说总体偏低;而当学习率设置为1×10-3时,经过前15轮训练的模型,测试精度均要高于1×10-5时的情况,但随着训练次数增加,会出现较大的波动,最终无论是少数类的AP稳定值,还是MAP稳定值均要低于1×10-5的情况。
损失函数值作为缺陷识别算法的重要部分,能够直观地反映出模型在训练过程中的收敛状况。如图5(a)所示,当学习率为1×10-2时,过大的学习率使得损失值趋于无穷大,已无法达到收敛;从图5(b)可知,当学习率设置为1×10-6时,损失函数值出现异常,经过50万次的迭代,模型仍无法收敛。学习率为1×10-3、1×10-4、1×10-5时,损失值随着模型训练的进行最终稳定在较低的值域范围内,并且在学习率为1×10-3与1×10-5这2种情况下的收敛情况十分接近,在前15轮训练中,收敛速率明显快于学习率为1×10-4的速度。

图5 不同学习率下损失值的变化曲线Fig.5 Variation curves of loss value under different learning rates
4.2 单倍辅助数据对实验结果的影响以及分析
为了验证本文的相关辅助数据样本对检测模型性能的影响,分别使用目标数据集和混合数据集训练模型,随后使用同一批测试集对经过训练的模型进行测试,得到如图6所示的P-R曲线。
根据图6可知:在添加相关辅助数据之前,正常类别数据样本占据极大优势,而缺陷类别,尤其是销钉松动类样本不足,导致检测模型在训练过程中侧重于学习正常类别样本特征,松动类的特征并没有得到有效的提取,最终松动类的AP值仅为0.64,而正常类别以及缺失类别的AP分别达到0.80、0.71。图7给出了类别失衡情况下缺陷类别的部分典型错分样本,在类别失衡的情况下,错分样本大多集中于少数类中,它们被错误地识别为数据占优的正常类别。在添加适量的人工采集的相关辅助数据后,尽管辅助数据样本与目标数据集之间存在一定程度的差异,但其在某种程度上缓解了类别不平衡所造成的“偏移”现象,即在保证正常类别AP变化不大的前提下,大幅度增加了缺陷类AP,其中松动类AP由原先的0.64上升为0.70,缺失类别AP也上升了0.3。
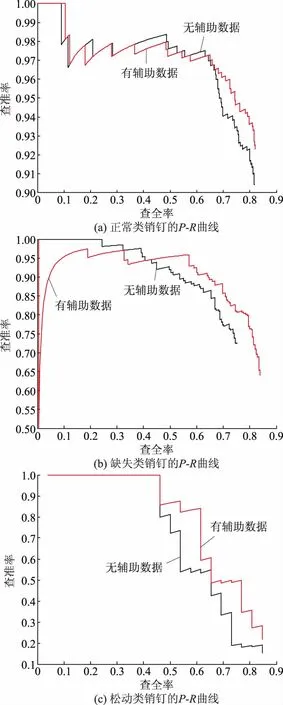
图6 对经过50轮训练的模型进行测试得到的各类别的P-R曲线Fig.6 Various P-R curves of the model tested by 50 rounds of training

图7 类别失衡情况下识别错误的缺陷样本Fig.7 Misidentified defect samples under category imbalance
4.3 辅助数据的量化实验及分析
为了进一步分析少数类的相关辅助数据的量对测试结果的影响,在原先的参数设置下,分别向原始目标数据集添加不同数量的辅助数据样本进行模型训练,最后使用同一批测试机对每一轮训练后的模型进行测试,得到图8所示的结果。

图8 AP与辅助数据样本数量的关系Fig.8 Relationship between AP and numbers of auxiliary data samples
根据图8测试结果可知:添加辅助数据后,模型在训练过程中可以学习到更多的松动类的特征,对松动类的重视程度有所提高,无论是MAP,还是少数类的AP,都有明显的提高。因此,当销钉缺陷数据样本数量不足以支持深度学习缺陷识别训练的情况下,可以通过添加相关辅助数据样本来提高模型的泛化能力。然而,当辅助数据样本数量达到原先少数类的5倍时,松动类的AP达到峰值0.80,MAP达到了最大值0.82;如果进一步增加辅助数据样本,鉴于目标数据集与辅助数据集之间存在某种程度的差异,当辅助数据样本的数量达到6倍,甚至6倍以上时,松动类的AP或MAP均有所下降。
为了分析目标数据集与辅助数据样本之间的差异性,以包含5倍辅助数据的训练集(记为A5)和不包含辅助数据集的训练集(记为A0)为研究对象,分别对前12轮训练输出的模型进行测试。对于前者,分别采用A5中只包含少数类(松动类)的辅助数据的测试集(记为T5)以及A5中只包含少数类的目标数据集(记为T6)进行测试,后者使用A0中销钉松动类作为测试集(记为T0)进行测试,输出图9所示的AP值变化曲线。
根据图9可以看出:由于辅助数据集无论是前景物还是背景,其复杂度均要低于无人机采集到的数据样本。因此,使用训练集A5经过1轮的训练后,在T5上就能够达到0.99的AP;但在T0和T6上AP要到达0.99,却需要经过多轮的训练才行。另外,通过图9中的曲线走势可以直观地发现模型在T0上的测试结果与在T5测试输出的曲线走势大致相同,并且后者曲线位于前者曲线上方,表明了辅助数据可以在某种程度上增强模型的泛化能力,但辅助数据样本与目标数据集之间的差异性对模型测试精度的影响也是不容忽视的。

图9 不同测试集下的AP值变化曲线Fig.9 AP value curves under different test sets
5 结束语
考虑到人工标注电力金具上销钉的常见缺陷时耗时耗力,并且经常出现漏检的情况,本文首先采用深度学习RetinaNet算法实现销钉缺陷的智能识别,并分析了学习率对实验结果的影响,为今后缺陷智能识别技术提供了理论依据;其次,针对销钉缺陷识别中缺陷样本不足导致的类别失衡问题,分析了类别不平衡给缺陷识别造成的影响,并得出结论:类别失衡致使大量松动类销钉被错分为数据量占优的正常类,设置合适的学习率以及迭代次数,不仅可以加快模型训练时的收敛速度,还可以在某种程度上缓解数据样本不足带来的不利影响,提高少数类的AP。另外,考虑到现实情况中销钉缺陷样本出现较少和采集代价高,本文提出了一种简单易行的相关辅助数据样本的采集方法,形成辅助数据样本库,为后续研究打下坚实基础;最后,考虑到人工采集到的辅助数据样本与无人机采集到的目标数据之间的差异,对相关辅助数据以及目标数据和辅助数据之间的差异进行了量化分析,结果表明对于少数类样本数量,添加适量的辅助数据有利于提高检测模型的泛化能力,但当辅助数据远远超过目标数据数量时,辅助数据中的冗余数据使得两者间的差异明显放大,致使检测模型的精度反而有所下降,不利于模型训练的开展。
本文虽然得出了AP与辅助数据样本数量之间的数据关系,但对造成这种结果的原因仍缺乏深入分析;同时,本文只是在数据层面展开研究,而在算法层面并未提出相应改进策略。因此,这些问题均可以作为后续的研究内容。
