基于多判据融合的用电信息采集系统异常数据甄别模型
2019-10-10祝永晋马吉科季聪
祝永晋,马吉科,季聪
(江苏方天电力技术有限公司, 江苏 南京 211102)
随着计算机、传感技术、通信技术的广泛应用,配电网运营监测业务的不断推进以及大量监测计量装置的部署,配电变压器(以下简称“配变”)台区监测获得了海量运行数据、用户用电数据及设备状态数据,对这些数据进行分析、挖掘、抽取与加工,实现配变台区安全经济运行、提升服务质量、拓展电量电费业务成为配电网面临的挑战[1-3]。需特别指出的是,用电信息采集系统配变台区监测获得的海量电网数据中存在约10%的异常数据,有必要对数据质量进行分析,甄别异常数据,为开展监测运营业务提供可靠、精确、有效的数据支撑[4-5]。
因计量装置故障、通信信号差、采集器故障、人为因素等原因,用电信息采集系统时间序列数据会出现异常值[6-10],从而影响用电信息采集系统数据质量,而数据质量的好坏很大程度上决定了模型分析结果的好坏。因此,在建立分析模型前对用电信息采集系统数据中的异常值进行检测甄别,是提高数据质量的重要途径。
目前采用数据挖掘技术进行时间序列数据异常值检测的方法较为成熟多样,文献[11]提出了通过统计学方法得到时间序列数据的概率分布函数和相应的纠偏函数来检测异常点。基于统计学的方法依赖海量样本的随机分析[12],且必须知道数据分布模型,因而该方法有很大的局限性[13]。文献[14]使用Mahalanobis距离和最小协方差矩阵对变压器油色谱检测数据进行异常值诊断。文献[15]使用基于数据集分割和距离的异常值辨识方法,该方法能较好地扩展到不同的数据集大小和维度;基于距离的检测方法对于某些全局异常点效果较好,但其距离函数和参数不易选择,不能检测出局部异常点。文献[16]使用基于聚类和核密度假设检验的方法,在样本量不多的情况下有较好的效果,但不适用样本量多、高维数据场合。文献[17]将人工神经网络(artificial neural networks,ANN)运用到异常值检测,ANN在处理小规模问题上有很好的应用效果,但对大规模数据场景效率较低,难以较好地解决参数训练问题,且训练过程易陷入局部最优,模型结构和权值设置不当还会严重影响模型精确度。文献[18]将用户历史最近24个月的用电量数据和信用评级作为分类特征,通过训练支持向量机(support vector machines,SVM)分类,获得了一定的效果;SVM具有更好的泛化能力,但在处理海量样本时有一定的难度[19-20]。
上述基于统计学原理的方法和传统的机器学习方法,在小样本、低维度的异常数据辨识任务中获取了不错的效果,但这些传统的学习方法如SVM、ANN通常难以在海量样本中进行训练,难以完成海量数据异常甄别的任务。相较于传统的机器学习,深度学习将训练集事先分成小批量数据进行计算,提高了训练效率,且深度学习在深层结构中能有效避免梯度消失或梯度爆炸的问题。因此深度学习方法更适用于学习电流、电压等海量用电信息采集系统数据的时变规律[21-22],从而进行异常值检测与甄别。采用深度学习的方法可解决传统机器学习方法在处理海量数据时所存在的占用内存高、运行处理速度慢及难以处理高维特征数据等问题。为此,本文主要以用电信息采集系统配变台区监测的电流、电压和有功功率数据为对象,研究运用深度学习技术的用电信息采集系统异常数据甄别模型;为避免单一模型在处理不同任务时的局限性,同时采用原型聚类法、密度聚类法和概率密度法等机器学习算法进行异常值甄别,以“4取2”的方法交叉验证,提升模型的异常点甄别能力,为运行监测业务提供精确的数据保障。
1 用电信息采集系统数据特性
用电信息采集系统中智能电表的电流、电压、有功功率、无功功率曲线中的异常数据直接反应了智能电表的运行状态,此类异常数据属于表计方面的测量异常点以及用户用电异常点。表计异常点较为隐蔽,一般存在较长时间,如数据持续缺失、偏大或偏小,其中,数据持续缺失问题可通过数据预处理统计发现。由于不同用户用电行为特征和用电数值大小有区别,对用电信息采集系统数据进行数据挖掘和异常甄别时,主要依赖该用户的用电行为产生的数据。若表计数据的变化规律与时序规律未发生改变,仅出现持续时间较长的数值偏大或偏小异常。在这种情况下,数据样本中包含表计发生该类异常之前的数据,通过数据挖掘的方法能寻找到异常开始发生的数据点;若此种情况下,数据样本中不包含表计发生该异常之前的数据,基于数据挖掘的方法很难从数据中甄别该异常数据,此时更加依赖基于电力系统模型的方法,如计算排查线损率等方法,但该方法需求的数据量与数据种类较多,工作量大,检测效率较低。本文运用数据挖掘领域的方法进行异常数据甄别,效率较高,但鉴于目前数据挖掘领域方法的局限性,本文主要讨论数据样本中此种表计隐蔽异常数据较少情况下的异常数据甄别。
2 基于多判据融合的用电信息采集系统数据异常值甄别方法
2.1 原型聚类模型
原型聚类法是对样本空间中具有代表性的点进行迭代更新求解的聚类方法,本文采用原型聚类模型中的k-means算法。原型聚类法异常值检测模型的输入与输出见表1,其中,i、u、P分别为电流、电压、功率的当前采样点实际值序列,Δi1、Δu1、ΔP1分别为电流、电压、功率当前采样点与前一个采样点的变化值序列,Δi2、Δu2、ΔP2分别为当前采样点与前两个采样点的变化值序列。该模型的输入是当前采样点的实际值与变化,主要检测当前实际值与当前变化趋势的关系;模型检测出的异常点距离各类聚类中心较远,这些点的当前实际值与当前变化趋势的关系异常。

表1 原型聚类法异常值检测模型的输入与输出Tab.1 Input and output of outlier detection model based on prototype clustering method
2.2 密度聚类模型
密度聚类法假定类别可以通过样本分布的紧密程度来决定,将样本分为密集样本类别和离散样本噪声点。密度聚类法异常值检测模型输入与输出见表2。该模型输入的是2个不同物理量实际值的序列,主要检测2个物理量之间的相关性;模型检测出的异常点和其他点相比密度不可达,这些点的2个物理量之间相关性异常。

表2 密度聚类法异常值检测模型的输入与输出Tab.2 Input and output of outlier detection model based on density clustering method
2.3 概率密度模型
事先难以判断现场实际测量的电压、电流及功率数据的概率分布类型,对电压、电流及功率等不同时间序列进行异常值甄别时,先采用核密度函数分别拟合其概率分布,并获得概率密度函数;由概率密度函数可获得变化值的正常范围。概率密度法异常值甄别模型的输入与输出见表3。该模型的输入是当前采样点的变化值序列,主要检测各采样点的变化程度;该模型检测出的异常点和其他点相比变化程度过大。

表3 概率密度法异常值检测模型的输入与输出Tab.3 Input and output of outlier detection model based on probabilistic density method
2.4 长短期记忆网络分位数回归模型
基于深度学习算法的异常值甄别模型中,由训练完成的深度学习分位数回归模型对未来的电流、电压和功率数据进行预测,获得多组预测值,求出时序数据的置信区间范围。若预测值偏离时序数据的置信区间范围,该点即为异常值点。本文在分析长短期记忆网络(long short-term memory,LSTM)基本原理的基础上,分别对电流、电压及功率建立LSTM分位数回归模型,实现对三者时间序列的异常值甄别[23]。深度学习异常值检测模型的输入与输出见表4,该模型的输入为历史数据序列,检测出的异常点与其他点相比不符合历史数据的时序变化规律。

表4 深度学习方法异常值检测模型输入输出Tab.4 Input and output of outlier detection model based on deep learning method
图1所示为LSTM各部分结构,计算过程分别如下[24]。
a)遗忘门计算过程如图1(a)所示,计算公式为
ft=σf(Wf·[ht-1,xt]+bf) .
(1)
式中:Wf、bf分别为遗忘门权重矩阵和遗忘门偏置;[ht-1,xt]表示将2个向量拼接;ht-1为前一时刻的LSTM输出;xt为当前时刻输入;σf为遗忘门激活函数。
b)输入门计算过程如图1(b)所示,计算公式为
it=σi(Wi·[ht-1,xt]+bi) .
(2)
式中:Wi、bi分别为输入门权重矩阵和偏置项;σi为输入门结构的激活函数。
c)当前时刻输入的单元状态c′的计算过程如图1(c)所示,计算公式为
(3)
式中:Wc、bc分别为该单元的权重矩阵和偏置项。

(4)
e)输出门的计算如图1(e)所示,即
ot=σo(Wo·[ht-1,xt]+bo) .
(5)
式中:Wo为输出门权重矩阵;bo为输出门偏置项;σo为输出门激活函数。
f)LSTM最终输出由输出门和单元状态共同决定,如图1(f)所示,即
ht=ot∘tanh(ct) .
(6)
建立LSTM模型后,分别训练对应于分位数0.01~0.99的99个LSTM分位数回归模型,预测得到99组预测曲线数据,计算得到置信区间范围。通过比较真实值与置信区间范围,确定最终的异常数据辨识结果,这样可以有效避免人为设置阈值对结果带来的不确定性。
在模型训练中,损失函数为分位数损失函数。LSTM回归模型的训练过程可看作是关于LSTM的权重参数W与网络结构偏置项参数b的优化问
题的求解,其目标函数为
(7)
式中:τ为分位数,τ∈(0,1);Y为模型训练集的输出;X为模型训练集中的输入样本;N为输入样本个数。
其中
ρτ(θ)=θ·[τ-I(θ)] .
(8)

(9)
式中θ为自变量。
在多判据融合模型中,原型聚类法检测当前采样点实际值与当前变化趋势的关系是否异常,密度聚类法检测电力系统中电压、电流、功率两两之间的相关性,概率密度法检测当前采样点与之前时刻采样点的变化值是否会过大造成突变异常,深度学习法检测当前的采样点数据是否符合历史数据的时序变化规律。4种模型的目标检测范围互补,通过“4取2”确定最终甄别结果,既能互相验证,降低误检率,又可以从不同的检测维度发现异常点,获得较高的正检率。

图1 LSTM各组成部分结构Fig.1 Structures of components of LSTM
3 基于多判据融合的用电信息采集系统异常数据甄别测试
3.1 用电信息采集系统异常数据甄别模型基本测试
测试分析的第一部分工作包括:基于正常运行计量装置采集的电流、电压、有功功率数据,在原始数据中增加不同程度的随机噪声,形成异常点;使用上述4种模型对含噪声数据进行测试,获得各个模型异常值检测结果。测试中,4种模型检测结果通过“4取2”策略确定最终的异常值检测结果,即4种模型中有2个或2个以上的模型判定待检测数据点为异常值,则该数据点的最终检测结果为异常,否则该数据点的最终检测结果为正常。
选取某一正常电表,时间范围为2017年7月1日至8月31日共计5 856点,其中有功功率均值为25.625 kW,最大值94.956 kW,最小值5.1 kW,变化平均值为2.866 kW;随机生成均值为0、标准差为13的共59个正态分布误差值,噪声点个数占时序数据长度的1%,并将这些干扰随机放入功率原始时间序列中。图2为实际功率序列及随机噪声序列。

图2 实际功率序列及随机噪声序列Fig.2 Actual power sequence and random noise sequence
采用4种模型进行异常值甄别测试分析分别如下。
a)基于原型聚类法的异常值甄别测试。由于原型分类法的分类个数k值需预先设定,经过多次模型测试,综合考虑聚类效果、噪声甄别效果以及运行时间等,选择以下参数:聚类类别为4类,异常值点判断准则阈值尝试设置为3.2,聚类最大循环次数为500,距离函数采用欧式距离。公式(10)表示聚类样本中任意第i个样本和第j个样本之间的欧式距离,每个样本有n维参数,其中Xi={xi1,xi2,…,xin} ,Xj={xj1,xj2,…,xjn}。
d(i,j)=
(10)
原型聚类功率分析结果如图3所示,其中纵坐标表示该样本与所属类别的聚类中心的相对距离。将该样本与所属类别聚类中心的实际欧式距离记为Lre,该聚类类别中所有样本与所属类别聚类中心的实际欧式距离的中位数记为Lme,则相对距离L=Lre/Lme.

图3 原型聚类功率分析结果Fig.3 Prototype clustering power analysis results
由图3可以看出,该方法的聚类效果较为明显,标为△的异常点明显与数据样本中大多数●的样本点分离;△异常数据点表示该采样点实际值与变化趋势的关系异常。
b)基于密度聚类法的异常值甄别测试。选择的参数包括:最大距离设置为0.5、样本点归一化范围为(0, 4)、1类别的最少样本个数为5、距离函数为欧式距离计算方法。密度聚类分析结果如图4所示。
由图4可以看出,该方法的聚类效果较为明显,功率、电流总体成线性关系,功率、电压平面分布在左下角。“☆”形符号表示的异常点明显处于数据样本中大多数“×”形符号样本组成的簇的边缘,“☆”异常数据点表示功率、电流相关性异常和功率、电压相关性异常。
c)基于概率密度法的异常值甄别测试。图5为采用该方法测得的功率变化值概率密度曲线。

图4 密度聚类分析结果Fig.4 Density clustering analysis results

图5 概率分布分析结果Fig.5 Probability distribution analysis results
由图5可以看出,功率变化值集中分布于0附近,结合概率密度函数,可以获得功率变化值出现某一值时的概率。假设功率变化值在0值附近某一范围内的概率为99.9%,则认为功率变化值在该范围内是正常的。此时可计算出功率变化值端点值为-10.464 6和10.462 8,即认为:正常功率变化值范围为[-10.464 6,10.462 8],不在此范围的即为异常功率变化,检测出的异常数据点的异常类型为功率数值变化率过大异常。
d)基于深度学习算法的异常值甄别测试。使用LSTM分位数回归算法对功率进行预测,获得待测时间点功率的概率预测置信区间范围,共同的网络结构参数设置为:4层循环神经网络,包括输入层(96×1序列输入),1层LSTM层(8节点),1层普通隐含层(4节点),1层输出层(1节点);输入与输出参数使用最近历史96点的数据预测下一时刻的电流值(采样间隔15 min);模型优化为RMSProp(带动量的随机梯度下降算法),迭代次数为400,训练批数512(训练样本一共5 856个,1次迭代约分为4~5批),训练样本中验证集所占比率为5%;对应不同的分位数回归模型,目标函数为对应的模型输出值与真实值的分位数损失函数。LSTM分位数回归结果及功率真实值如图6所示,横坐标为数据点序号,纵坐标为功率值大小。对应图例,实际值为实际的功率值曲线,预测值为对应于0.5分位数模型的预测值,图例中100%CI为预测的100%置信区间范围,对于不同类型的数据,可以选择不同的置信区间范围作为阈值范围。本文经多次测试实验,综合甄别检出率和误判率考虑,采用100%的置信区间范围作为阈值。

图6 LSTM分位数回归结果及功率真实值Fig.6 LSTM quantile regression results and true power values
由图6可以看出,实际值曲线基本在100%置信区间之内,且置信区间范围比较窄;说明LSTM分位数回归模型预测功率的置信区间的效果较好,并且区间范围对异常甄别有很好的参考价值。超出阈值置信区间范围的异常点为不符合历史数据样本的时序规律的采样点。
对于本文提出的异常甄别模型,采用检出率kacc和误检率kerr作为评价指标,即
(11)
式中:NT为正确检测的异常点个数;NF为错误检测的异常点个数;Nb为实际异常点个数。改变检测时间序列数据类型,添加不同大小方差的噪声,进行多次异常数据检测,异常数据检测结果见表5。
由表5可以看出,在不同聚类方法中,概率密度法的检出率最高,密度聚类法的检出率最低;同时,概率密度法对于变化值最敏感,误检率最高;LSTM分位数回归模型的性能相对于这些聚类方法,有较为明显的提升,检出率指标和误检率指标均更好;基于多判据融合的异常数据甄别模型的甄别效果相比LSTM分位数回归模型的甄别效果有所提升,平均检出率能达到本文所述方法最高的76.27%,同时具有最低的平均误检率17.23%。
3.2 实际电表的电流和功率测试结果
为了验证基于多判据融合的用电信息采集系统数据异常甄别模型在实际用电曲线序列中的效果,取3只异常电表A、B、C,对2017年3月6日至2017年5月7日共计5 952点A相功率值序列、电压值序列和电流值序列组成原始数据集进行异常甄别,对模型检测出的异常点进行曲线相关性研究分析,检验异常数据甄别模型是否有效,检测具体情况如下。
a)电流变化率过大异常。对电表A在5月7日的电流曲线数据(如图7所示)进行异常甄别,确定第37点为异常点。由图7可以看出,在第37点处电流变化值较大,判定为异常值点,异常原因为电流突变异常,异常数据甄别有效。
b)功率变化率过大异常。对电表B在5月7日的功率曲线数据(如图8所示)进行异常甄别,确定第57点为异常点。由图8可以看出,在第57点处功率变化值较大,判定为异常值点,异常原因为功率突变异常,异常数据甄别有效。
c)电流功率相关性异常。对电表C在5月7日的功率曲线及电流曲线数据(如图9所示)进行异常甄别,确定第75点为异常点。由图9可以看出,在75点处,电流和功率相关性,显著异常,判定为异常值点,异常数据甄别有效。
实际电表测试出的异常甄别结果可反馈给有关部门进行分析,若某一电表在一段时间内多次检测出异常点,则它有较高的异常嫌疑;若它在某一较长的时间段内只有1个异常点,也可比对异常点发生前后的数据,排查是否发生了数值偏大或偏小的隐蔽表计异常。该模型为主动排查异常用电计量装置提供了可靠的依据,有效缩小了排查范围,有很高的参考价值。

图7 电表A电流及电流变化值曲线Fig.7 A ammeter current and current change curve

图8 电表B功率及功率变化值曲线Fig.8 B ammeter power and its change curve

表5 异常数据检测结果Tab.5 Detection results of anomaly data
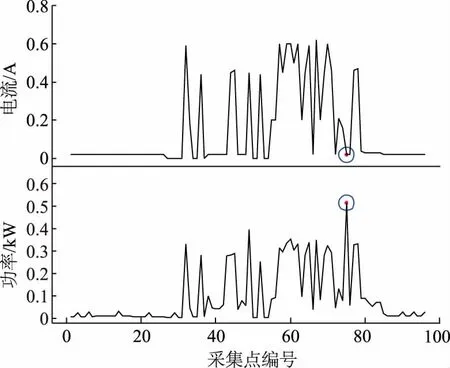
图9 电表C电流及功率曲线Fig.9 C ammeter current and power curve
通过算例分析,得出以下结论:
a)基于LSTM分位数回归算法的异常数据甄别模型具有可行性和有效性,在人工添加噪声的模拟异常曲线检测中,平均检出率达到74.58%,平均误检率为21.18%。
b)基于多判据融合的异常数据甄别模型具有有效性,且该模型检出率和误检率指标水平较基于LSTM分位数回归算法的异常数据甄别模型有进一步改善。在人工添加噪声的模拟异常曲线检测中,平均检出率达到76.27%,平均误检率为17.23%。
c)本文所提方法在人工添加的异常曲线和实际运行故障的异常曲线中,均能有效检测异常数据点,表明了该方法用于模拟检测具有可行性,本文建立的用电信息采集系统数据异常甄别模型具有实用性。
4 结论
为了验证本文提出模型对于异常数据甄别的检出率和误判率,向正常运行工况下的用电信息采集系统时序数据中添加正态分布噪声,构建并模拟用电信息采集系统系统异常数据。
本文建立的基于LSTM分位数回归的用电信息采集系统数据异常甄别模型,实现了对智能电表历史运行曲线的有效学习,运用深度学习技术挖掘历史时间序列数据特征,建立历史数据与待检测数据之间的映射关系,进而对测试时间点智能电表运行曲线进行更为精确的概率预测,获得更为准确置信区间范围;将其与实际曲线进行对比,从而寻找出异常点。人工添加噪声的时间序列数据测试证明了该算法的有效性。
本文建立了基于多判据融合的用电信息采集系统数据异常甄别模型,通过原型聚类法、密度聚类法、概率密度法和深度学习方法分别检测,运用“4取2”方法交叉验证,提高了异常点甄别检出率,降低了异常点甄别的误判率,提升了模型的异常点甄别能力,为运营检测业务提供精确数据保障,有助于供电企业进行抄核收工作,减少用户和供电企业经济损失。
