无衍射光莫尔条纹的中心定位方法

2019-10-10丁善婷翟中生李劲松黄娇洁吕清花王选择

应用光学 2019年4期

丁善婷，程壮，翟中生，李劲松，黄娇洁，吕清花，王选择

(1.湖北工业大学机械工程学院,现代制造质量工程湖北省重点实验室，湖北武汉 430068；2.湖北工业大学理学院，湖北武汉 430068)

引言

无衍射光因为其中心光斑大小、形状不随传输距离发生变化而备受关注[1-2]。随着人们对无衍射光研究的不断深入，无衍射光应用的领域也越来越广泛，如激光加工[3]、景深延拓[4]、3D形貌测量[5-6]、表面粗糙度测量[7]等。同心圆光栅莫尔条纹具有较好的计量和放大特性，在精密测量领域中应用广泛[8-10]。由于无衍射光形状与同心圆光栅相类似，利用两束无衍射光干涉生成无衍射光莫尔条纹，不仅保留了同心圆光栅莫尔条纹的优点，而且引入了无衍射光的特性。

无衍射光莫尔条纹由于兼具无衍射光和莫尔条纹的优点，引起了人们越来越多的关注及研究。赵斌、张新宝等人提出来一种利用无衍射光和环形光栅重叠产生环状莫尔条纹测量空间直线度[11-12]，并以此为基础研制了无衍射光莫尔条纹直线度测量仪[13]以及准直、跟踪、定位系统[14]。作者对无衍射光莫尔条纹也进行了大量研究，利用无衍射光莫尔条纹测量大行程工作台四自由度运动误差[15]，将直角棱镜与半透半反镜作为运动单元置于工作台，建立四自由度运动误差模型，通过CCD中光斑中心的位置变化计算运动误差。

实现无衍射光莫尔条纹的精确定位，对测量结果的精度有很大的影响。目前对单束无衍射光定位的方法已经比较成熟，常见的方法主要有光强重心法、最小二乘圆拟合、圆环滤波、混沌蚁群算法、相关因子法等[16-18]。由于无衍射光莫尔条纹相比较于单束无衍射光，形状更加复杂，实现无衍射光莫尔条纹的定位更加困难。目前对无衍射光莫尔条纹定位的方法主要是：对生成的无衍射光莫尔条纹进行计数，通过莫尔条纹数与两光斑中心的位置关系反推光斑中心位置[19-20]。此方法利用了莫尔条纹的计量性与放大性，通过对莫尔条纹进行精确计数，求出两光斑中心位置。由于莫尔条纹的质量对计数结果影响很大，定位精度不高；而且需要运用图像的全部数据进行分析，运行速度较慢。

本文提出了一种无衍射光莫尔条纹两光斑中心同时定位的方法。通过对无衍射光莫尔条纹的特征分析，提取并检测局部同心圆环区域，结合均值聚类，并进行异常点删除，求解出较为精确的两光斑中心位置，实现无衍射光莫尔条纹的中心定位。

1 理论分析

1.1 特征介绍

无衍射光莫尔条纹是由两束无衍射光干涉而成。单束无衍射光的外形具有同心圆特征，利用边缘信息，能较好地实现单束无衍射光定位；而无衍射光莫尔条纹包含椭圆莫尔条纹族和双曲线莫尔条纹族，外形比较复杂，定位比较困难。分析两者的特征相关性，如图1所示，相关特征主要体现在光斑中心附近。

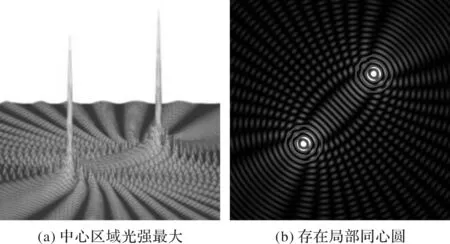
图1 无衍射光莫尔条纹特征

1) 中心区域光强最大。无衍射光莫尔条纹具有两个中心区域，单独分析其中一个中心区域，和单束无衍射光一样，也具有光强最大的特征，所以同样利用灰度值的大小可以找到两个中心区域的大致位置。

2) 存在局部同心圆环。无衍射光莫尔条纹虽然整体外形呈辐射状分布，但是两个中心区域部分都存在局部同心圆特征，所以利用这个特征可以较精确地找到两个中心区域的光斑中心，实现无衍射光莫尔条纹的中心定位。

1.2 处理方法

1.2.1 提取局部同心圆环区域

具体步骤如下：

1) 中值滤波。选取大小为S的邻域进行中值滤波。中值滤波能较好地去除椒盐噪声，对去除高斯噪声也有一定的效果。实现去噪效果的同时保留图像的边缘信息。

2) 直方图均衡化。采用直方图均衡化处理的作用是通过拉伸图像像素强度范围增强图像对比度，将不同光照强度下的灰度范围均衡到0～255，减弱外界环境对实验结果的影响。

3) 阈值分割并二值化。为了保持高定位精度的同时加快运行速度，选取靠近两个中心光斑的局部同心圆环进行分析。选取合适V值，以(255-V)作为阈值对图像进行二值化处理，得到无衍射光靠近其光斑中心局部同心圆环区域。其中局部同心圆环区域所包含的同心圆环个数以3～6为标准。

4) 形态学处理。分割后的图像会产生零散的小面积连通区域，在不影响无衍射光莫尔条纹的两光斑中心的局部同心圆环整体轮廓的前提下，删除面积小于S1的连通区域，此时得到的图像为I1。然后采用大小为P的圆盘形结构元素I2对图像I1进行先腐蚀后膨胀的开运算，开运算的计算公式为

I1·i2=(I1$I2)⊕I2

(1)

式中：$为腐蚀操作；⊕为膨胀操作。最后再次删除因开运算使图像产生的面积小于S2的新连通区域，得到图像I3。

1.2.2 局部同心圆环检测

针对图像I3，首先采用Sobel算子进行边缘检测。分别选用大小为H，水平方向的内核Gx和垂直方向的内核Gy与图像I3进行卷积运算，则在图像的每一点的灰度G大小为

(2)

然后对处理后的图像采用Hough圆变换。Hough变换是图像空间和参数空间之间的一种变换，能有效检测出直线、圆、椭圆等。为了简述其原理，令需要检测圆的参数方程如下

(3)

式中：a、b为圆心的横纵坐标；r为半径。

假设(x1,y1)为圆上一点，则过点(x1,y1)的所有圆可以表示为(a1(j)、b1(j)、r1(j))，同理过(x2,y2)、(x3,y3)、…,(xi,yi)的所有圆可以表示为(a2(j)、b2(j)、r2(j))、(a3(j)、b3(j)、r3(j))、…、(ai(j)、bi(j)、ri(j))。如果其中有n个点，当存在已知圆(am、bm、rm), 使得am、bm、rm等于n个点中所有对应的a(j)、b(j)、r(j), 则可以判断这n个点同在圆(am、bm、rm)上。

Hough变换检测圆时，需要根据图像的实际情况选取合适的半径步长R0、角度步长θ、最小圆半径R1、最大圆半径R2。其中经过多次实验可知当R0为1 pixel，θ为0.1 rad能满足绝大多数情况。由于单个局部圆环区域最多含有6个同心圆环，且同心圆环间距d0与中心光斑半径r0是确定的(只与生成无衍射光元器件参数有关)，则取R1为(d0+r0)、R2为(6d0+r0)即可。通过参数的选取，并对边缘上的点进行统计计算，确定可能存在的圆，得到初始圆心集C0(x,y)。

1.2.3 圆心集聚类分析

对初始圆心集C0(x,y)进行聚类分析。K-means聚类属于一种无监督的机器学习，将相似的对象归到同一簇。它是一种硬性算法，是典型的基于原型的目标函数聚类方法的代表，它以数据点到类别中心的某种距离之和作为优化的目标函数，利用函数求极值的方法来得到迭代运算的调整规则。

K-means聚类是使用误差平方和SSE作为聚类的目标函数，当SSE最小时，聚类效果最好。给定数据集X，其中只包含描述属性，不包含类别属性。假设X包含K个聚类子集X1、X2、…,Xk，各个聚类子集的样本数量分别为n1、n2、…、nk，各个聚类子集的聚类中心分别为m1、m2、…、mk，则误差平方和准则公式为

(4)

式中：Xi是第i个聚类子集；p是Xi中的样本点；mi是Xi中所有样本的均值。

因为无衍射光莫尔条纹是由两束无衍射光干涉而成，所以存在两个聚类子集。令K=2，此时会随机选取两个点作为初始聚类中心，通过计算每个圆心点到初始聚类中心的欧式距离，将每个圆心点分配给距离其最近的聚类中心，则聚类中心以及分配给它们的圆心点就代表一个聚类。所有的圆心点都被分配完成后，两个聚类子集会根据新的聚类计算聚类中心，当没有聚类中心发生变化时，此时误差平方和最小，为最优聚类，从而能较好地将上述步骤的圆心集C0(x,y)分为两组圆心集C1(x,y)和C2(x,y)。

1.2.4 删除异常点并迭代

对检测到的两组圆心集C1(x,y)和C2(x,y)求取其中心点O1(a,b)和O2(a,b)作为初始中心。计算每组圆心集中每个圆心点到其初始中心的距离，令最大距离为dmax，以初始中心为圆心，R为半径，半径R所形成的圆要包含各自圆心集的集中部分，以包含各自圆心集的85%像素点为标准，R取值为0.85dmax，删除在圆以外的点即异常点。对新的圆心集再次求取中心点，重复迭代w次(不超过3次)，保证每次迭代要包含当前圆心集85%像素点，得到O3(a,b)和O4(a,b)，即为较为精确的两束无衍射光中心。

2 结果分析

2.1 仿真结果

针对上述的无衍射光莫尔条纹处理方法，在Matlab中生成含有椒盐噪声和高斯噪声的无衍射光莫尔条纹，用来模拟实验中含有噪声的无衍射光莫尔条纹，其中椒盐噪声的密度为0.02；高斯噪声的均值为0，方差为0.02。选取4组中心位置确定的无衍射光莫尔条纹，利用上述方法进行处理，结果如表1所示。图2为第一组数据的莫尔条纹定位仿真图。

由表1分析可得到，4组数据的平均误差能控制在1 pixel内，所以利用上述方法实现无衍射光莫尔条纹的中心定位，具有较高的定位精度。图2中单束无衍射光的r0为8 pixel，d0为12 pixel，则参数的选取为S=3×3 pixel，V=195，S1=100 pixel，I1=1 pixel，S2=60 pixel，H=3 pixel，Gx=[-1 0 1; -2 0 2; -1 0 1]，Gy=[-1 -2 -1; 0 0 0; 1 2 1]，R1=20 pixel，R2=80 pixel，R=10 pixel，w=2。

图2 莫尔条纹定位仿真

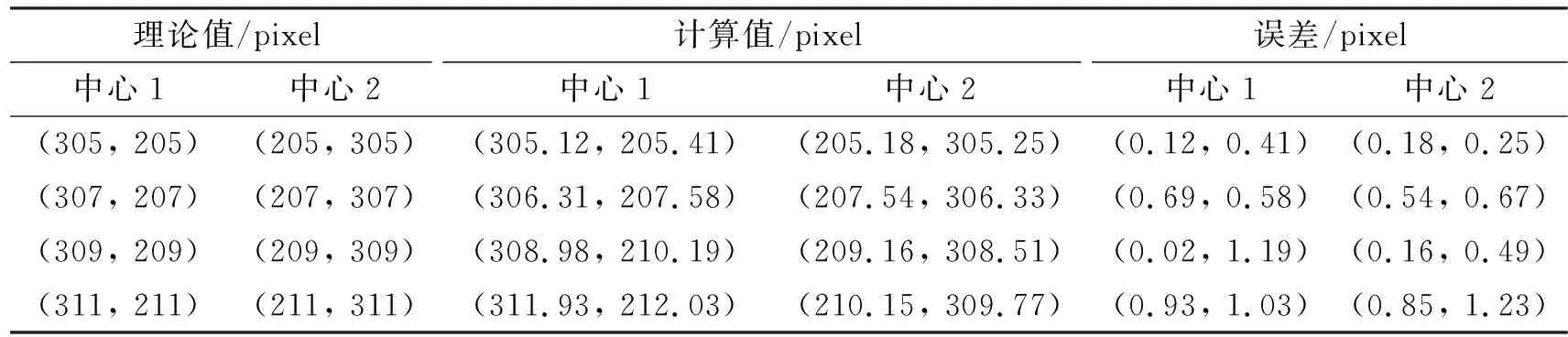
表1 理论与计算数据

2.2 实验结果

两束无衍射光干涉会产生莫尔条纹，实验中将生成的无衍射光经过分光棱镜变为两束无衍射光，令两束无衍射光发生干涉现象，从而形成无衍射光莫尔条纹。

从图3可以看出拍摄出来的莫尔条纹呈辐射状分布，明暗条纹的间隔有时不明显，会影响条纹计数的精度。由于生成的无衍射光的r0与d0与仿真相近，则参数的选取大致与仿真部分相同，不同的是V=5，S1=1 000 pixel，I1=2，S2=300 pixel，R=6 pixel。利用此方法计算的中心位置为中心1(577.12, 637.06)、中心2(632.50, 460.57)，放大中心光斑到一定程度后的初始估计中心分别为中心1(577, 637)、中心2(633, 460)。对比理论结果与实际结果，其误差控制在1 pixel内，和仿真结果一样，说明该方法具有较好的精确性。