离轴非球面零位补偿检验的非线性畸变校正

厉宏兰，袁吕军，徐节速，李 倩，康 燕

(1.中国科学院国家天文台 南京天文光学技术研究所，南京 210042;2.中国科学院天文光学技术重点实验室(南京天文光学技术研究所)，南京210042;3.中国科学院大学，北京 100049)

引言

离轴非球面具有大视场、无中心遮拦及像质接近衍射极限等优点，使其在空间光学系统的应用越来越广泛[1]。由于对离轴非球面元件在口径、波段、精度、质量以及材料等方面的应用要求越来越高，实现离轴非球面元件的高精度光学检验是制造离轴非球面光学系统的核心[2-3]。

目前，零位补偿法是大口径离轴非球面终检阶段的常规方法[4]，常用的辅助光学元件有Offner补偿器、Dall补偿器及计算全息(CGH)等，但无论是使用补偿透镜还是二元衍射元件，面形图都存在一定的面形特征位置偏移和尺寸畸变[5-6]。为了校正零位补偿器引起的畸变，一般采用图像校正法更为简便，大致分为4种[7-11]：一是使用基准蒙片标定校正畸变，但是基准蒙片的制作和安装过程比较复杂，容易破坏镜面结构；二是控制移动检测平台的移动来加入离焦项，通过离焦和球差的变化来反解检测系统中的图像畸变，该方法反解推导繁琐且移动距离不易精确控制；三是通过仿射变换推导映射函数进行畸变校正，但是推导过程中利用的镜面特征点较少，不能实现畸变校正结果与镜面的高精度对准；四是利用干涉测量中的Fiducial功能标定畸变，此法采集的样本点数量不够多,校正精度不高。本文提出了一种在被测元件旋转对称情况下适用的简单有效的畸变校正方法，通过在离轴非球面上标记等间距环带并利用matlab算法对干涉仪采集到的图像进行处理，确定图像的畸变中心，然后对光线追迹数据进行拟合，重构离轴镜的面形误差位置分布图，从而实现非线性畸变校正，并用此法指导了520 mm×250 mm离轴非球面镜的小磨盘数控抛光，数控精抛坐标准确，面形误差收敛效果明显。

1 Offner补偿检验及畸变

1.1 Offner补偿器的检验过程

通常情况下，为了简化光路结构和节约制作成本，将Offner补偿器设计为两片式，即补偿镜和场镜。其中补偿镜起补偿初级像差的作用，场镜不仅将补偿镜成像在非球面上还承担少部分的高级像差的补偿[12]。离轴非球面镜的检验光路由4D动态干涉仪、Offner补偿器及离轴非球面反射镜3部分组成，检验时由干涉仪发出的球面波光束射入Offner补偿器，变成与待检非球面匹配的非球面波前，沿法线入射的波前经待检非球面反射后再次经补偿器转变成球面波进入干涉仪，与干涉仪的参考波前形成干涉检验，测得的面形误差等高图显示了待检非球面与所需表面之间的偏差[13-15]，检验光路示意图如图1(a)所示，实物图如图1(b)所示。

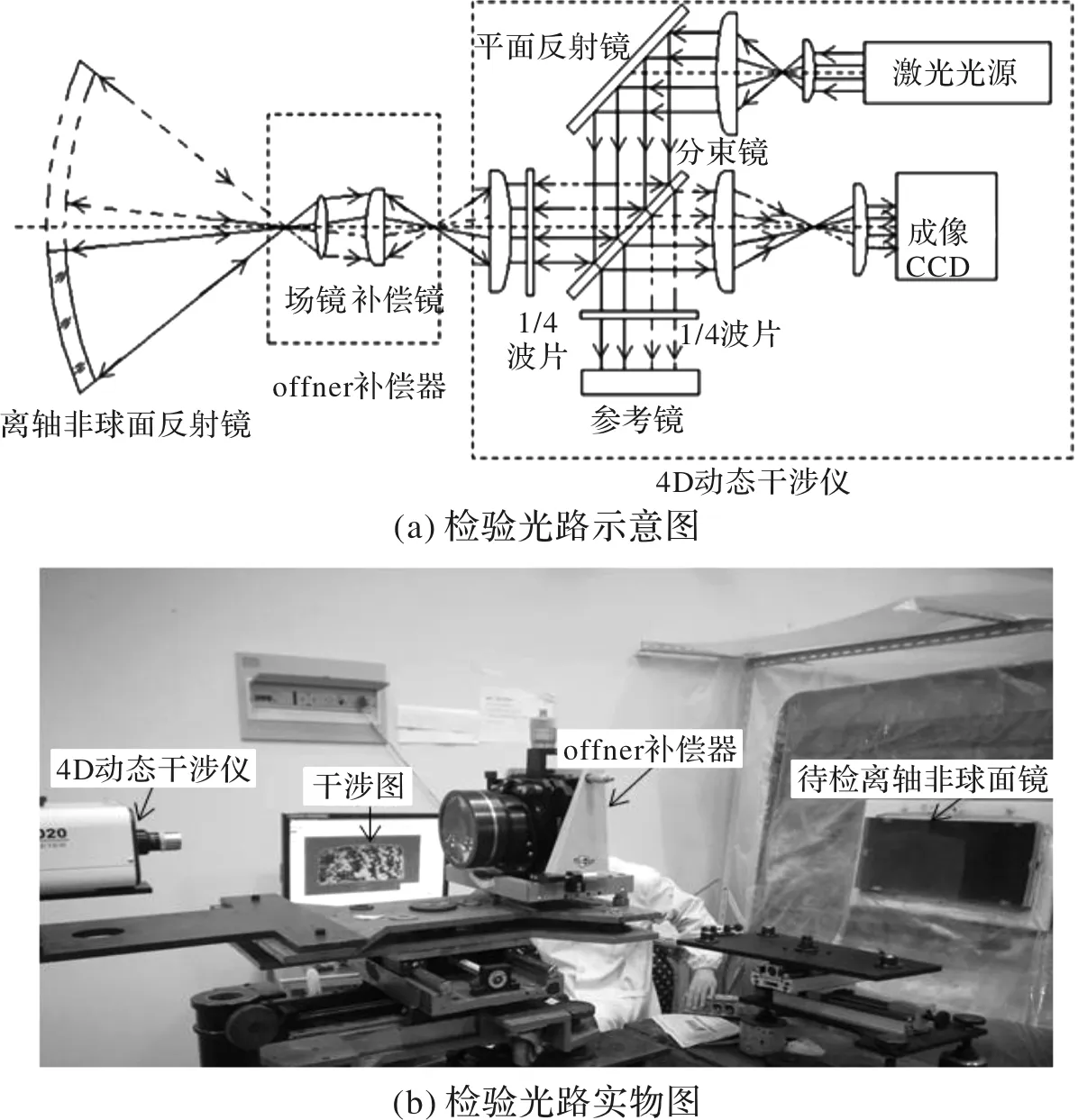
图1 离轴非球面检验光路图

1.2 畸变的产生及影响

本文中Offner补偿器系统结构参数如表1所示，由光路设计结构可知，整个检验光路较短，而被检镜口径较大，第一面到第四面的半口径缩小了2.5倍，使入射光线经Offner补偿器后急剧压缩汇聚，光线发生大角度偏转，引起各环带面型特征非线性偏移，导致小磨头抛光工作坐标点定位出现偏差，驻留时间计算不准确，收敛速度减慢等问题。

表1 补偿器系统结构参数

针对本文中520 mm×250 mm离轴非球面镜的补偿器光路进行光线追迹，光线追迹的归一化入瞳坐标范围为：PX为[-0.7,0.7],PY为[-1,1]。畸变产生的影响如图2所示，图2(a)中的A1B1C1D1为由近轴光线追迹得出的理想像面的镜面坐标，A2B2C2D2为由实际光线追迹得出的实际像面的镜面坐标。很显然，在同等坐标刻度和归一化入瞳坐标下，实际像面存在较大的畸变，并且畸变图关于光轴中心O点是完全对称的，在畸变的对称中心小范围内基本无畸变，畸变的大小与镜面坐标点离对称中心的距离有关，距离越远畸变越大[16]，因此确定畸变中心是关键。本文中离轴非球面镜补偿光路的畸变主要考虑径向畸变，相对畸变的大小可以表示为

(1)

式中：P表示相对畸变；Rreal表示实际坐标相对于畸变中心的径向位置；Rparaxial表示近轴坐标相对于畸变中心的径向位置。由于被测元件是旋转对称的，所以可以取整个像面坐标的1/4计算相对畸变的大小，即图2(a)中OHB2I所围成的部分。经计算，整个母镜实际像面的最大相对畸变约为30%，但由于离轴非球面镜(离轴量为160 mm)只取了母镜的一部分，即图2(a)中DEFG所围成的矩形，其最大近轴径向位置为385.778 4 mm，因此该离轴镜在补偿器光路中产生的最大相对畸变约为15%左右，畸变曲线图如图2(b)所示。

图2 畸变示意图和曲线图

2 非线性畸变校正

由图1的光路图可知，本文中的离轴非球面镜与系统光轴有一定的夹角，所以镜面坐标到干涉仪中的图像坐标是一个很复杂的映射函数。设实际镜面面形为fmirror(xm,ym),经补偿器光路一次折射后被检镜波前为fo(xo,yo)，干涉仪面形检验结果图像为fimg(xi,yi)，标准面形图为fstd(xs,ys)，则：

fmirror(xm,ym)=G*fo(xo,yo)

(2)

fimg(xi,yi)=β*fo(xo,yo)

(3)

式中：G为实际镜面面形到一次折射后被检镜波前的映射函数；β为一次折射后被检镜波前到干涉仪面形检验结果的放大率，因此只要确定畸变中心和映射函数就可对干涉仪面形检验结果图像进行映射变换，然后对其插值处理就可得到标准面形图fstd(xs,ys)，畸变校正流程如图3所示。

图3 畸变校正流程图

图4 环带示意图

2.1 确定检验图的畸变中心

在只考虑径向畸变的情况下，对加工坐标系下的离轴非球面以离轴镜母镜顶点为圆心标记等间距环带，含环带标记的镜面通过Offner补偿器光路后经干涉仪成像后发生旋转和畸变，利用MATLAB算法对该图像进行技术处理，提取各环带的圆心坐标，寻找各环带拟合的畸变中心的最佳位置，即该图像的畸变中心。

设各环带间隔为a，环带数量为n，则各环带的半径分别为r1，r2，r3，…，rn，其中r2=r1+a,r3=r1+2a，…,rn=r1+na。在实际操作中，环带间隔越小，环带数量越多，对径向畸变的描述越准确，镜面环带示意图如图4所示。经补偿检验后得到含环带标记的干涉图fimg(xi,yi)，利用MATLAB算法对其进行采样处理，提取各环带的圆心坐标。设畸变中心O点坐标为(x0,y0)，各环带的圆心坐标分别为(x1,y1)，(x2,y2)，…，(xn,yn),为了寻找畸变中心O点的最佳位置，设U={x1,x2,x3,…,xn}，V={y1,y2,y3,…,yn}，算法流程如图5所示，求畸变中心的最佳纵坐标y0同理。

由于离轴非球面镜检验光路的特殊性及工件摆放位置与干涉仪的CCD有相对旋转，干涉图不但存在畸变而且围绕畸变中心O点发生旋转，如图6所示。设检验时镜面绕系统光轴的夹角为θ，则干涉仪面形检验结果图像也需绕畸变中心O点旋转一个角度θ至图像关于畸变中心对称，旋转变换的矩阵为

(4)

式中：x,y,z为图像旋转前的坐标；x′,y′,z′为图像旋转后的坐标；θ为图像旋转的角度。

图5 算法流程图

图6 畸变边界图

2.2 确定映射函数

在大口径、快焦比离轴非球面镜的检验光路中，由于干涉仪采集的局部面形残差位置与被测光学元件实际位置不对应，小磨头抛光工作点定位出现偏差，影响抛光精度及效率，因此准确地描述映射函数至关重要。由于一次折射后被检镜波前fo(xo,yo)与干涉仪面形检验结果图像fimg(xi,yi)是倍数关系，因此可以用fmirror(xm,ym)与fo(xo,yo)的拟合结果来表示映射关系G。本文利用光学设计软件对其进行光线追迹，采样间隔为0.01。设实际镜面fmirror(xm,ym)的归一化径向位置为ρm，一次折射后被检镜波前fo(xo,yo)的归一化径向位置为ρo，采用多项式来拟合光线追迹结果，相应的映射关系可以表示为

(5)

归一化拟合曲线图和拟合误差曲线图分别如图7和图8所示。由图8可知，多项式拟合误差始终在1 μm以内上下波动，满足数控小磨盘抛光的精度要求。

图7 归一化拟合曲线图

图8 拟合误差曲线图

3 离轴镜校正实例

本文中520 mm×250 mm离轴非球面镜的主要参数有：顶点曲率半径R为1 200 mm，离轴量为160 mm，倒圆角半径为25 mm，圆锥曲线k为-1。利用上述校正方法对干涉仪成像产生的畸变图进行畸变校正并对其进行二维插值处理，畸变校正结果如图9所示，上方为初始面形图及初始网格图，下方为畸变校正图及校正网格图。与原始测量数据相比，经过上述方法校正后的面形图无论是在各环带面形特征位置上还是在轮廓上都更接近被检镜面的真实形状，但仍存在较小的畸变校正误差[17]。由畸变校正结果可知，位于母镜边缘处的镜面畸变最大，因此在镜面边缘处和局部面形残差处取100个样本点计算偏差大小。本文将畸变校正误差定义为样本点在畸变校正面形图上的位置坐标与实际测量的镜面位置坐标的偏差[18]，可以表示为

(6)

式中：(xD,yD)为畸变校正面形图上样本点的位置坐标；(xmirror,ymirror)为实际测得的镜面上样本点的位置坐标；Q为畸变校正误差。经计算，最大偏差为0.859 1 mm,偏差平均值为0.424 9 mm，偏差曲线图如图10所示。通过数控小磨盘抛光实验，发现抛光工作点坐标吻合率在90%以上，满足小磨盘抛光的工作要求。

图9 畸变校正结果

为了验证该校正方法指导小磨盘数控准点位置抛光的有效性，在终检阶段前半部分抛光周期中干涉仪检验结果图直接用于抛光，在后半部分抛光周期中先对畸变图进行校正和重构后再指导抛光。图11中前300 h的波动曲线呈现出一种效率低、收敛慢的趋势，而后半部分的面形误差呈现出明显单调递减趋势，抛光位置坐标准确，有良好的收敛特性。其中，抛光的工艺参数如温度、压力、抛光周期、驻留时间等在这两个抛光周期中几乎是相同的[19-20]。

图10 偏差曲线图

图11 抛光实验收敛曲线

4 结论

针对大口径、快焦比离轴非球面的零位补偿检验过程中干涉仪检验结果图像出现畸变和偏转的问题，提出了一种基于同心环带和光线追迹的畸变校正方法，首先利用同心圆标记和matlab算法确定畸变中心，再运用光学设计软件的光线追迹结果描述映射关系G，校正后图像的面形尺寸精度满足数控小磨盘抛光时工作点的定位精度，同时该方法适用于各种自由曲面的面形尺寸校正，是一种简单实用的畸变校正方法。运用此方法对某一光学系统的520 mm×250 mm离轴抛物面主镜的补偿检验结果图进行坐标畸变校正，有效解决了各环带的非线性压缩变形问题，镜面误差收敛速度快，最终离轴抛物面主镜的面形PVq值达到了0.151 28 λ，RMS值达到了0.024 3 λ。