层析法计算三维物体全息图的并行加速研究

肖 波,郑华东,2，刘柯健，李 飞，高智方

(1.上海大学 精密机械工程系,上海 200444；2.教育部先进显示与系统应用集成重点实验室，上海 200444)

引言

计算机生成全息技术(CGH)是一种利用具有光学全息数学模型通过计算机辅助生成数字全息图的技术。尽管CGH可通过计算机技术快速实现，但仍需要大量耗时的计算复核，这对计算机生成全息图的速率产生了很大的瓶颈。为了解决这些问题，已经提出了各种方法。贾甲提出通过使用压缩表法降低计算复杂度和减少内存存储空间以提高速度[1]，Yoshikawa提出使用泰勒展开近似方法降低计算复杂度，以提高计算速度[2]。H. Shimobaba利用现场可编程门阵列(FPGA)的硬件和图形处理单元(GPU)硬件进行加速处理[3-4]，蒋晓瑜教授等人利用查表法对电源法数据压缩加速[5]。2018年，国防科技大学辛诚提出利用CUDA(compute unified device architecture)实现基于GPU环境的matlab计算全息图的加速计算像息图快速计算[6]。宁苒提出采取GPU的matlab计算全息图[7]。

虽然Shimobaba提出的硬件加速算法可以大幅提高运算速度，但是该方法具有以下限制：开发FPGA板的成本很高，开发时间长且需要专业的FPGA的处理知识。而通过matlab调用库函数计算无法充分发挥GPU底层计算资源，还有进一步的优化空间。同时，由于已经有很多方法对计算全息的点源法和三角面片法进行了加速处理，本文使用层析法计算三维物体全息图的方式以CUDA C进行程序编写，通过对线程和存储架构优化，并通过流处理方式掩盖数据传输的延时时间，对菲涅尔衍射算法进行最大幅度的优化以获得最快的计算速率，对计算全息进行了数值模拟和光学再现以获得三维物体计算全息图的再现像。对GPU加速计算分析表明，使用GPU并行计算比传统CPU串行运算速度有大幅提高，并且随着处理的切片数据量的增加优势更加明显。

1 计算全息计算原理

1.1 全息的基本原理

计算全息术是一种利用光的干涉和衍射特性显示的技术。光全息显示可以用图1来说明。利用从物体反射或者透射的携带了物体信息的物光波传播到记录平面(xh,yh)，其在记录平面上与参考光波干涉叠加的复振幅分布称为物光O(xh,yh)，照射到记录平面的另一束光称为参考光R(xh,yh)，全息图就是物光和参考光干涉的条纹分布；全息再现过程也利用了光的衍射原理，当光波照射到全息记录介质时，将再现和还原之前保存的原物的记录信息。

图1 光全息记录光路原理图

1.2 基于层析法的计算全息原理

首先通过计算机软件模拟三维物体数据模型可以得到光波的数学描述。根据处理过程的不同，分为点源法[8]、三角面片法[9]和层析法[10]。然后通过对物体或者波面进行离散抽样出样点计算出物光波在全息平面上的复振幅分布。最后可以把全息平面上的光波复振幅分布编码成全息图透过率变化，在空间光调制器上进行再现[11-13]。

本文使用的是层析法进行全息图计算，该方法认为一个三维物体可以离散为一系列垂直于Z轴的多层平行的截面，如图2所示。每一个平面图形是一个二维数组，可以方便地利用快速二维傅里叶变换计算其衍射光波的分布，然后计算每个平面的衍射光波，最后将所有平面的物光波叠加并抽取其相位信息，最终平面上叠加的相位信息就是我们需要得到的全息图数据结果。

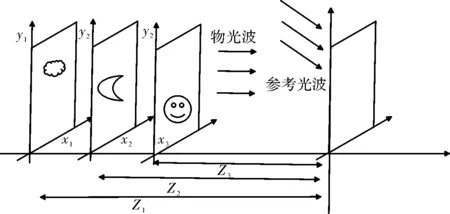
图2 层析法计算三维物体全息图的原理图

将物体沿法线方向分为N层，第n层平面图与全息图平面距离为zn，振幅透射率为fn(x,y)，则其在全息记录平面上的衍射分布菲涅尔近似为[14]

(1)

其中：k为波数，k=2π/λ；xh、yh为全息图平面坐标，On(xh,yh)表示物面第n层的复振幅。

三维物体各个层面衍射到全息面的复振幅之和为

(2)

考虑到人眼结构的分辨率[15]，为了得到连续的再生像，相邻之间的距离Δz必须小于人眼的纵向分辨距离。人眼的最小分辨距离公式为

(3)

人眼的分辨角ε=2.9×10-6z2rad，瞳距为Le=65 mm，则可以计算出相应三维物体的最小分割层数。

2 CUDA并行计算

2.1 GPU计算原理

CUDA(compute unified device architecture)是NVIDIA推出的一个基于GPU通用计算的并行计算处理平台和编程模型[16]。利用图形处理器(GPU)多处理单元的编程特性，通过大量的线程并行实现计算性能的显著提高。一个GPU具有多个流多处理器簇(streaming multiprocessors, SM)，如图3，每一个SM都分别设置有独立访问纹理内存(texture memory)、常量内存(constant memory)和全局内存(global memory)及它们的总线，并通过里面的多个流处理器(streaming processors, SP)共享控制逻辑和指令缓存[17]。全局内存具有千兆字节(GB)的数据传输带宽，但是具有较长的读取时间延时，SM能够在4个时钟周期内访问共享缓存，访问全局缓存则需要400～600个时钟周期，为了提高处理和计算速度和处理瓶颈，通常需要将GPU和CPU进行流并行处理异步计算[18]。

2.2 基于层析法快速计算

为了实际使用全息图，快速计算CGH非常重要，通常CGH需要消耗大量的计算时间[19]。对于1 024×1 024分辨率的10 000个点光源的3D物体，全息图需要大约十亿次计算，为了减少计算时间，我们使用了GPU并行处理。图4显示了中央处理单元(CPU)和GPU的结构差异。

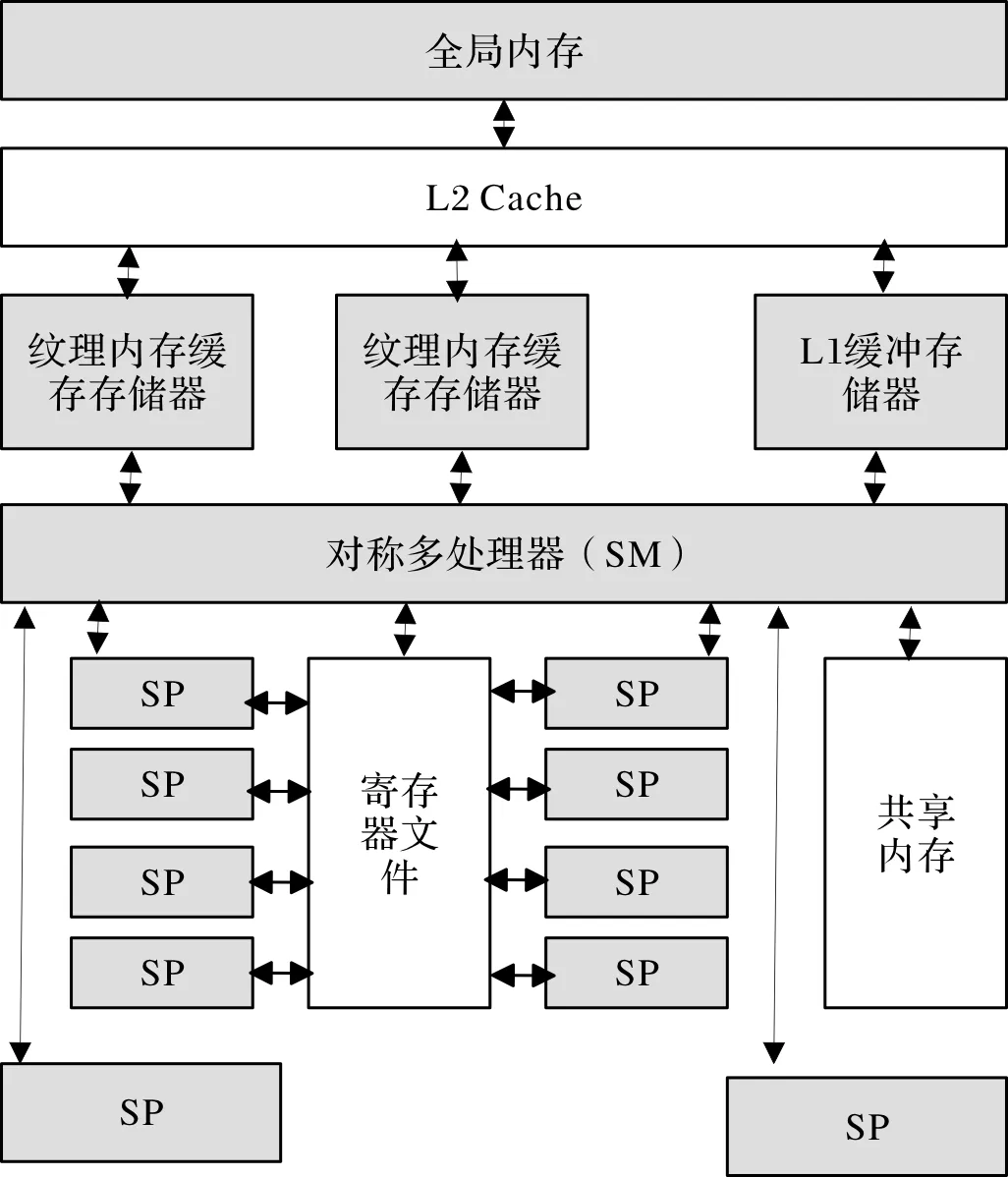
图3 SM内部组成结构图

图4 CPU架构和GPU架构示意图

如上所述，GPU的并行计算能力远超过CPU，因为GPU拥有比CPU多几个数量级的运算核心。因此许多研究已经使用了GPU快速计算复杂算法，在本文中，我们使用了CUDA是因为CUDA比OpenCL更容易实现CGH运算算法。如图5所示，先通过对三维物体计算分层，提取出每一层次的截面信息，然后分配线程块和内存，对各个截面层次的图像信息进行迭代并行计算，并同步进行各个分层的全息图的合成，最终得出三维物体的衍射全息信息。

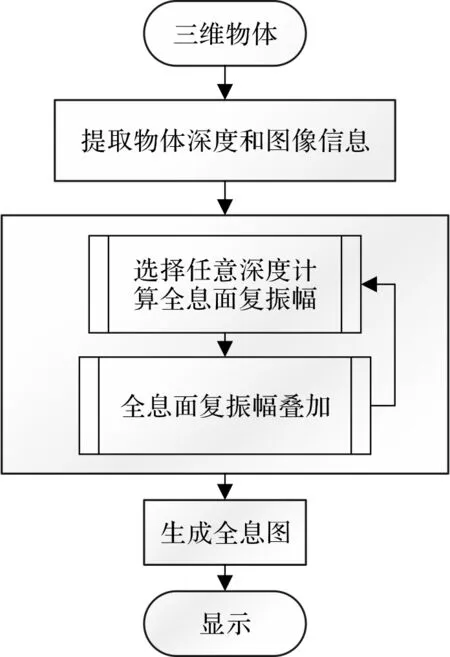
图5 GPU并行处理步骤

在一定条件下，可知菲涅尔衍射近似公式(4)可以看作为一个二维傅里叶变换的过程：

(4)

其中：F{·}表示傅里叶变换；x0、y0为衍射面的坐标；x、y为观察面的坐标。如果对公式做变形推导，可以得出只要求一次的傅里叶变换的离散求解，称为S-FFT算法(single fast Fourier transform algorithm)，如(5)式所示。其中：Δx、Δy是衍射面x方向和y方向上的抽样间隔；Δx、Δy是观察面x方向和y方向上的抽样间隔；m0、n0、m、n分别为衍射面和抽样面的抽样点数，且m0=1,2,…,M0，n0=1,2,…,N0。

(5)

通过利用GPU流多处理器优化算法执行和数据传输过程(其示意图如图6所示)，使得全息图运算时间和物点信息的传输时间达到稳定的平衡点。同时还可以使用CUDA线程优化的方法来优化硬件资源的分配，实现的关键代码如图7所示，通过CUDA流处理掩盖传输延迟，提高运算速率[20-21]，还可以优化算法的执行顺序进行异构计算等方式进一步提高其计算速度。由于GPU计算瓶颈主要有带宽、内存和浮点数运算能力，而全息图计算时，主要性能瓶颈存在于带宽。因此将菲涅尔变换算法分为2个核函数分开进行流处理，以覆盖存储传输时的延迟。将菲涅尔算法分为传输运算二维傅里叶变换和结果累加计算两个部分。

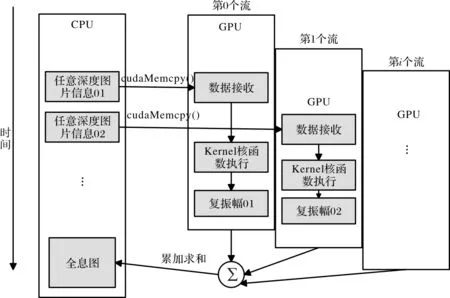
图6 GPU流处理计算示意图

GPU并行处理层析平面数据示意图如图8所示，根据二维图像像素点划分为一个个线程矩阵进行计算。

图7 GPU端部分加速代码

3 实验结果与讨论

本次实验采用的硬件平台为Intel Core i5-3470，运行内存为8 G，实验显卡为笔记本显卡，参数为NVIDIA GeForce GT1050Ti，显卡的计算能力为6.1，显存4 G。如表1所示。

实验显卡为笔记本独立显卡有768个核心，最大计算频率为1.62 GHz，内存处理频率为3 504 MHz。

图8 基于层析法的CUDA并行化示意图

表1 硬件环境

采用层析法计算三维物体全息图的算法结果如图9和图10所示，可以知道硬件并行加速计算三维模型的数据的正确性，同时通过光电全息平台进一步验证了并行计算程序的可行性。在此基础上，分别通过GPU和CPU运算采集其计算速度，结果见表2。

图9 300 mm距离下512×512分辨尺寸再现效果

图10 层析法计算三维物体计算全息图结果数值仿真及光电再现验证

表2显示了不同分辨率尺寸下的三维模型在一定分层数量时所花费的时间和加速比。可以看出，经过优化后，随着图片切片的增加，在GPU端流处理并行运行节省的时间也大幅增加，增加了1个数量级。

表2 CPU和GPU计算方式的计算时间和计算效率

4 结论

本文通过对层析法进行GPU的加速研究，在GPU并行计算方法下，对三维模型分层切片同时优化硬件资源和算法，再使用流处理的传输策略有效加快了计算全息图生成速度。分析了不同分辨率和不同分层情况下的加速计算效率，基于GPU的全息图并行加速计算方法比基于CPU串行计算方法的计算效率提高66倍左右。该方法为三维显示计算全息图的快速计算提供了有益的参考。