基于后向散射法测量蒸汽湿度反演算法的优化

胡青松，黄章俊，唐振洲，袁志超

(1.长沙理工大学 能源与动力工程学院，湖南 长沙 410114；2.湘潭大学，湖南 湘潭 411105)

引言

火电厂凝汽式汽轮机的末级大部分都是处于湿蒸汽状态下工作的，湿蒸汽的存在不仅会使汽轮机组的损失明显提高，降低整个机组的热效率，同时还会对处于湿蒸汽中高速旋转动叶片造成长期冲击侵蚀，引起叶片断裂，发生安全事故[1-2]。因此，实现对湿蒸汽各项参量实时准确的测量，对整个汽轮机组的安全经济运行具有重要的意义。

光学法是随着激光技术与计算机技术的不断发展而被开发出来的一种可以实现实时连续监测，操作方便的蒸汽湿度测量方法[3-4]。它是以Mie散射理论[5]和lambert-beert定律[6]为基础建立的理论数据，再用理论数据与CCD相机捕获的散射光强分布进行反演寻优，获取湿蒸汽的各项参数，进而求得蒸汽湿度[7]。因此，反演寻优的精度、效率以及稳定性都会对整个测量过程以及测量结果产生重要影响。

现阶段反演算法较多采用传统的均匀搜索算法和人工鱼群算法。均匀搜索算法是在各参量的取值范围内，通过设置步长，在整个解空间寻找最优解，这就导致步长设置的大小会严重影响搜索精度和搜索速度。如果步长设置过大，会导致搜索精度降低，而步长设置太小，又会导致搜索时间大大增加，搜索速度降低。人工鱼群算法适应范围广，且具有较快的收敛速度，但是其所得结果精确度不高[8-9]。粒子群优化算法是一种基于进化技术的群体智能理论的优化方法，在迭代进化的过程中，种群中的粒子之间的合作和竞争，从而使得粒子群优化方法具有收敛速度快、精度高、稳定性好等特点[10,13]。

本文提出在激光后向异轴角散射法基础上建立优化模型，采用粒子群算法对仿真数据和实验数据反演寻优，并与人工鱼群算法和传统的均匀搜索法进行比较，验证了粒子群算法在激光测量湿蒸汽参量中的有效性和可行性，弥补了人工鱼群算法和均匀搜索算法中的不足，为湿蒸汽参量的测量提供了更加可靠精准的数据和方法。

1 蒸汽湿度测量模型及理论

激光后向异轴角散射法测量湿蒸汽参量是以Mie散射理论为基础，通过CCD相机采集激光在湿蒸汽中某一角度的散射光强来实现的。测量模型横截面如图1所示。图中中间圆形横截面物体为模拟汽缸，在汽缸的左右水平方向以及右边向上倾斜30°方向上均设计有圆形孔，并由透明玻璃密封。激光由右边圆孔射入，在汽缸内遇到湿蒸汽发生光散射，在右上方圆孔处由CCD相机接收散射光强信息。

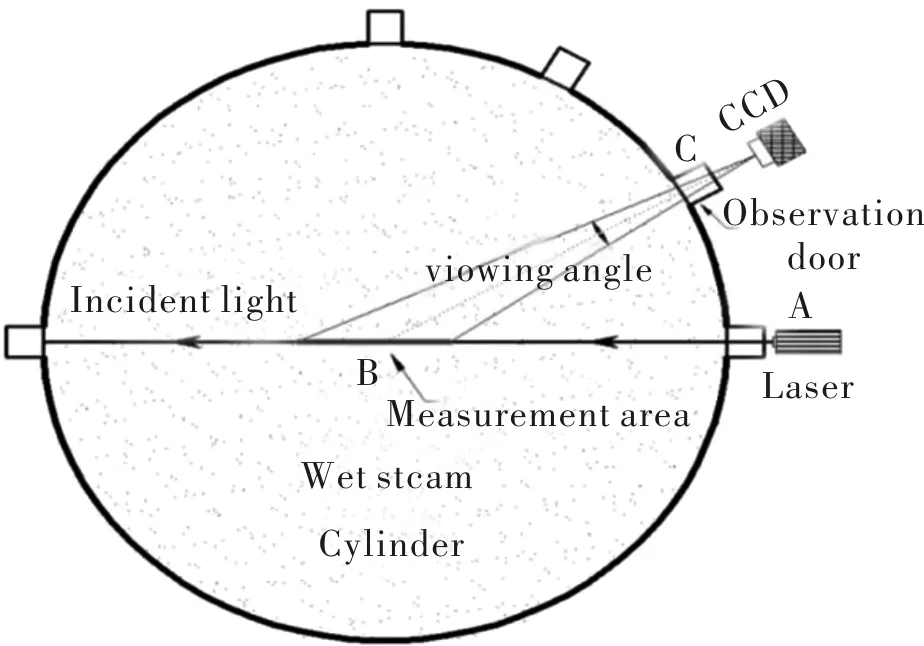
图1 湿蒸汽测量模型

CCD相机由纵横排列的多个像元组成，每个像元都对应不同散射立体角范围内的散射区域。假设汽缸内湿蒸汽水滴之间的距离足够大，各自不发生复反射，只发生单次散射，水蒸气对可见光的吸收系数为零，且均匀地分布在整个汽缸内，则可以把CCD相机接收到的散射光强当成是单个水滴散射光强的线性叠加，采用Rosin-Rammler函数(简称R-R分布函数)来描述气缸内湿蒸汽水滴微粒的分布。

当入射光为非偏振光时，激光器发出的激光到达探测器共经历衰减(A→B)、散射(B)、衰减(B→C)3个过程，发生衰减的过程遵循lambert-beer定律，发生散射的过程遵循Mie散射理论。假设入射光强为I0，l1和l2分别为为入射光线从气缸入口到散射区(A→B)及散射区到CCD相机(B→C)的距离，则散射角为θ时散射光强为

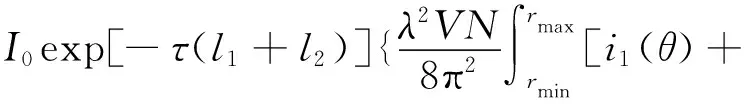
i2(θ)]sin(π-θ)Δφf(r)dθdr}

(1)

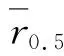
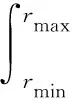
(2)

式中Qext表示消光系数，其公式为

(3)

式(2)中f(r)表示Rosin-Rammler蒸汽水滴尺寸分布概率密度分布函数，其公式为

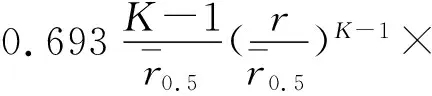
(4)

式(1)中Δφ与θ的关系式为

(5)

2 湿蒸汽参数反演优化模型

本文针对蒸汽发生器内部蒸汽湿度测量参数的反演问题，以理论光强值与实际光强值的最少二乘拟合偏差最小为优化目标，建立相应的湿蒸汽参数反演优化模型[11-12]。具体如下:

Iθi=I0exp[-τ(l1i+l2i)]×

sin(π-θi)Δφf(r)dθdr}

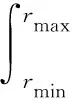
Δφ=

式中：X表示寻优参量；F(X)为目标函数；Iθi表示第i个像元接收到的理论散射光强；Ii表示第i个像元接收到的实际散射光强；θi表示第i像元散射立体角中心线与入射光之间的夹角；l1i和l2i分别表示第i个像元的入射光线从气缸入口到散射区以及散射区到CCD相机所经过的距离；i1(θi)和i2(θi)为由Mie系数求得的对应散射角θi的散射强度函数；θ1i和θ2i表示与第i个像元对应的散射立体角的起始角度和终止角度；n表示CCD相机纵向像元数；其余各参量的含义与式(1)～(4)相同。

3 粒子群算法寻优流程

在对湿蒸汽参量进行优化过程中，为了在较短的时间内搜索到满足搜索精度的结果，同时又满足搜索稳定性的要求，本文提出了利用粒子群算法[13-15]进行反演寻优，并且将反演结果与均匀算法和人工鱼群算法的结果进行对比。

粒子群算法寻优流程如图2所示。具体步骤如下：

1) 设定初始参数，包括种群数量、终止迭代次数n、惯性权重、参数量、参数取值范围。

2) 随机产生初始种群。

3) 利用实际测量值和目标函数计算公式，计算目标函数值F，找出最优个体。

4) 如果目标函数值F小于设定值T，则记录最优个体参数值，寻优终止；如果F大于T，则其他个体追逐最优个体，位置发生移动，记录寻优代数i=i+1。

5) 如果i-1大于n，则记录最优个体参数值，寻优终止；如果i-1小于n，则转到第3)步继续寻优。

终止条件是，当目标函数值满足小于设定值T=10-36时，即认为此时的反演参数已经满足反演结果精度要求。当目标函数值满足精度要求时，系统将自动结束寻优，并以此参数作为反演的最终结果。

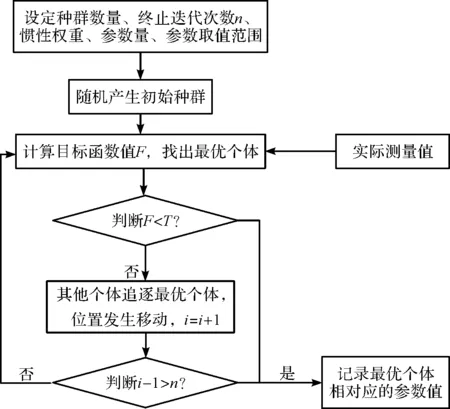
图2 粒子群算法寻优流程

4 3种算法反演结果对比

4.1 粒子群算法反演结果

在进行Mie散射理论公式运算时，公式非常复杂，且需要经过大量的循环递推过程，计算机进行运算寻优时非常耗时[16]，不利于在实际生产中实时获得测量结果。为此，利用三次样条插值函数，对寻优的参量设置合理步长，在保证数据精确性的前提下，还能大大提高系统的运行速度[17]。因此，本文将用三次样条插值函数代替复杂耗时的Mie散射理论公式。由于在实际测量过程中，环境中的各种因素都会对测量产生干扰噪声，因此在理论数据中本文将模拟环境因素加入高斯白噪声。

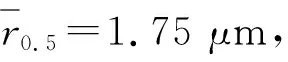
表1 粒子群算法反演结果

4.2 鱼群算法寻优结果

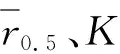
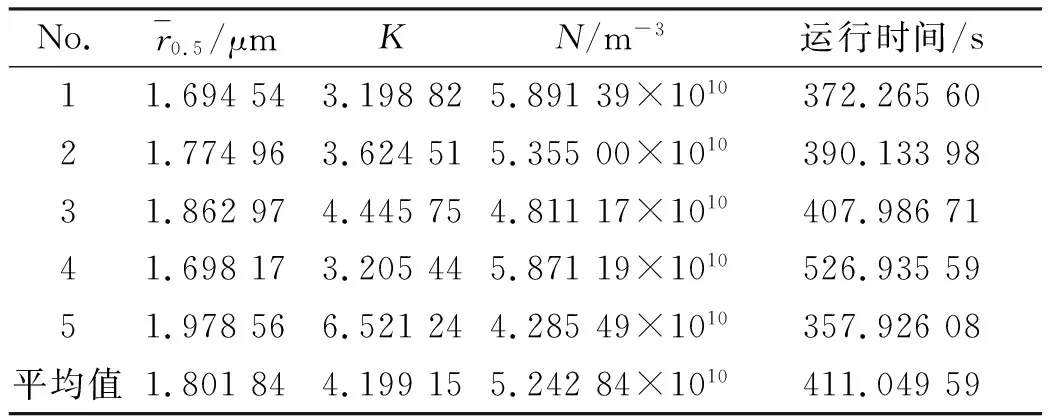
表2 鱼群算法反演结果

4.3 均匀搜索法寻优结果

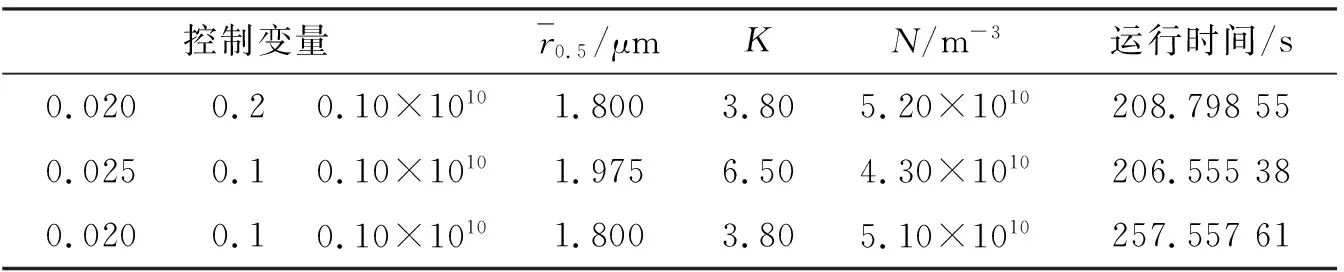
表3 均匀搜索反演结果

续表3

4.4 3种算法反演结果对比

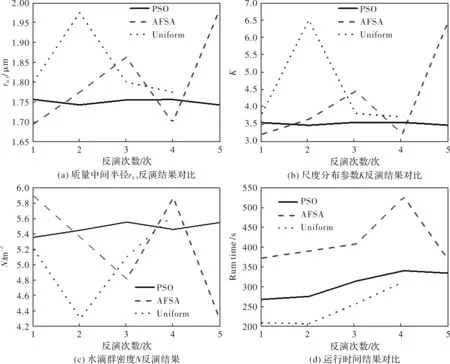
图3 反演结果对比

根据表1、表2、表3，结合图3(a)～3(d)可知，粒子群算法可以在较短的时间内反演出精度高且稳定的反演结果。人工鱼群算法和均匀搜索方法在相同设定条件下的反演结果误差比粒子群算法更大，反演时间相对更长，并且表2中的粒子群算法的第5组数据和表3均匀搜索的第2组数据的反演结果出现了较大的偏差，这说明鱼群算法和均匀搜索的反演结果精确度不高，且伴随着一定的随机性，并不总是能在整个解域范围内搜索到最优解，且均匀搜索受步长限制较为明显。通过对图3的反演数据进行分析比较发现，粒子群算法不但可以克服传统均匀搜索方法搜索步长和搜索速度的矛盾，在搜索时间相同，甚至是搜索时间大大减少的情况下，仍然能够得到比人工鱼群算法和传统均匀搜索方法更为精确的搜索结果。因此选择粒子群算法进行湿蒸汽参数反演算法可使反演精度更高，反演结果更稳定，运算时间更快。

5 粒子群算法反演寻优

按照图1后向异轴散射法建立的模型和上文的理论计算公式可计算得出图4反演数据散射光强曲线和图5反演数据尺寸概率分布密度曲线。第一次搜索得到的粒子群算法优化过程图如图6所示。

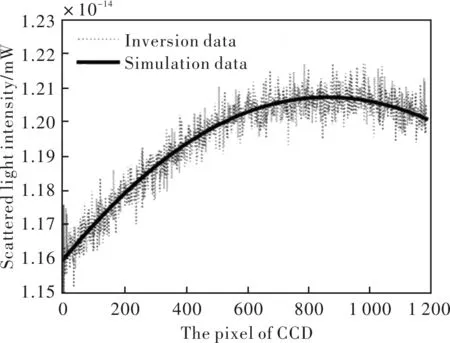
图4 散射光强曲线

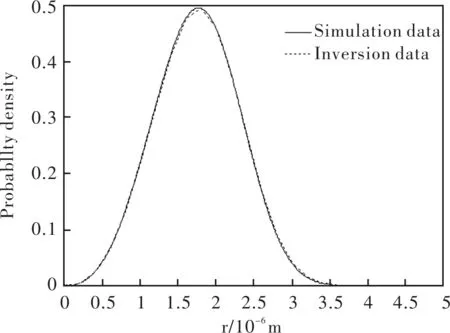
图5 水滴粒径分布曲线

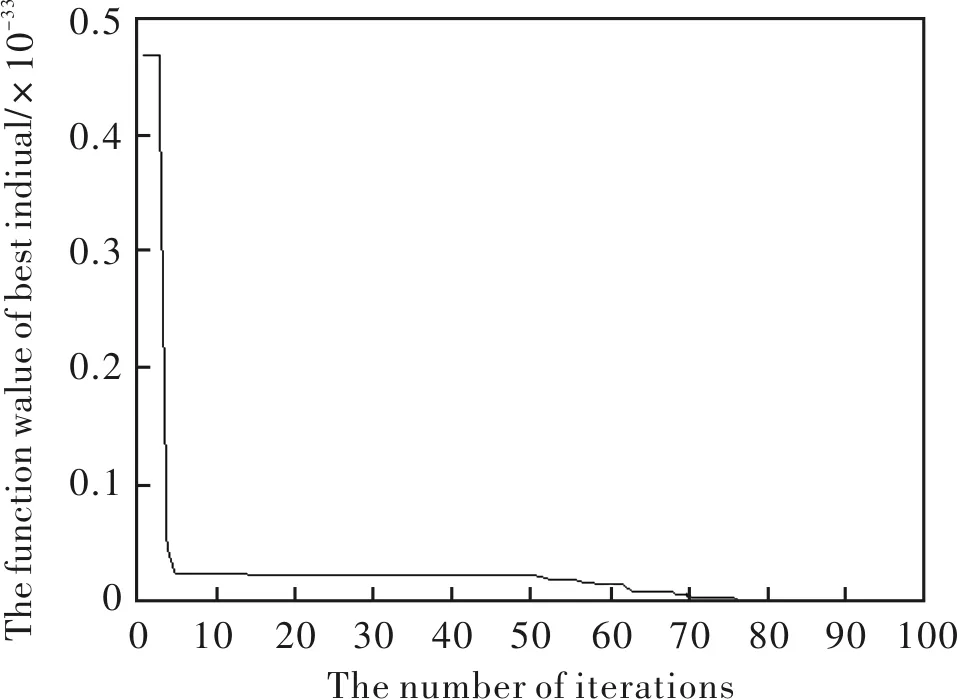
图6 粒子群算法优化过程

通过图4和图5中模拟数据曲线与反演数据曲线对比可以发现，模拟和反演过程图形变化非常吻合，进一步验证了反演结果的准确性。根据仿真数据得出的上述结果表明，利用粒子群算法能够在很短的时间内获得可靠的寻优结果，并且能够有效避免陷入局部最优解，全局寻优结果相当稳定。

为了验证粒子群算法不仅对模拟数据能进行反演，而且对实验数据也同样能进行有效且精确的反演，本文利用分辨率为1 600×1 200 pixels的CCD相机在表4所示稳定工况条件下拍摄到的实验散射光图，如图7所示。使用Matlab软件读取CCD相机纵向第800列像元(纵向中间线)接收到的散射光强，对散射光图进行滤波处理，并利用粒子群算法对其反演寻优，得到实验条件下的湿蒸汽参数。再基于湿蒸汽参数和上文所提的湿蒸汽测量模型，利用Matlab软件运算得到反演数据散射光强。实验数据与反演数据散射光强对比结果如图8所示。

图7 实验散射光

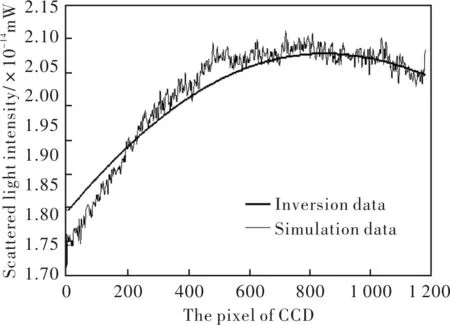
图8 反演数据与实验数据散射光强对比

表4 稳定工况湿蒸汽参数

通过图8的实验数据和反演数据散射光强对比可以发现，在实验过程中，实验所测的散射光强度曲线并不光滑，呈震荡型变化。这是因为在实验过程中，模拟汽缸中的湿蒸汽水滴颗粒粒度并不是均匀的，粒度大小变化呈多值性，再加上实验过程中存在噪声等环境因素，从而导致实验测得的散射光强呈现震荡变化。实验结果与反演数据在前半段的重合程度并不高，在接近500像素点的位置时才逐渐开始重合，并在第800列像元位置处同时达到最大值。主要由于CCD相机的响应需要一定的光强积累，所以就出现了在图像的前半段，两组散射光强数据交替上升，而在后半段吻合程度逐渐提高。综上所述，两条数据线基本吻合，验证了粒子群算法能够精确且有效地对实验数据进行反演寻优。

本文针对蒸汽发生器内部蒸汽湿度测量参数的反演，以理论光强值与实际光强值的最少二乘拟合偏差最小为优化目标，建立相应的湿蒸汽参数反演优化模型，对不同工况采集到的图像进行对比，图像灰度值变化趋势基本与稳定工况时保持一致，以均值滤波方法对图像进行处理后，用Matlab读取CCD相机纵向第800列像元(纵向中间线)上的灰度值，对CCD相机进行标定得到光强与灰度值的比例因子，以粒子群算法对不同工况条件下测得的实验数据进行反演，通过反演得到的散射光强随像元位置的变化曲线与实验测量得到的散射光强曲线比较吻合，表明在变工况条件下粒子群算法对实验数据处理同样有效。

6 结论

通过蒸汽湿度测量模型以及湿蒸汽参数设定值，获得仿真数据，再利用粒子群算法和蒸汽湿度参数反演寻优模型，对仿真数据进行多次反演寻优，结果表明：

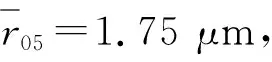
2) 利用粒子群算法对进口压力为0.58 MPa，出口压力为0.22 MPa，进口温度为158℃，出口温度123℃，汽比容为0.801 018 m3/kg，水比容为0.001 063 3 m3/kg的稳定工况下所拍摄的的实验图像进行反演计算，对比实验数据散射光强和反演数据散射光强发现，两条数据线基本吻合。对不同工况采集到的图像进行对比，灰度值变化趋势与稳定工况时基本一致，表明在变工况条件下粒子群算法对实验数据处理同样有效，验证了粒子群算法能够精确且高效地对实验数据进行反演寻优。