基于RBF神经网络与代数法的6R机器人逆运动求解
2019-10-10邓庆文胡泽启李轶峰
吴 强,邓庆文,胡泽启,李轶峰,邵 坦
(1.武汉理工大学 汽车工程学院,湖北 武汉 430070; 2.武汉理工大学 现代汽车零部件技术湖北省重点实验室,湖北 武汉 430070;3.湖北三环锻造有限公司,湖北 谷城 441700)
6R机器人是面向工业领域的多关节机械手或多自由度的机器装置,其自动执行工作,被广泛应用于各个行业。但由于作业对象的多样化,6R(六自由度且所有运动副均为转动副)机器人需迅速进行调整,以适应不同复杂形状下的轨迹规划任务。其逆运动学的求解精度和效率是决定机器人完成工作的精度和效率的重要因素。6R机器人的逆运动学求解常用的方法有代数法[1-3]、几何法[4]和数值迭代法[5]等。这些方法大多存在一些局限性,代数法需求解非线性方程组,计算量大;几何法的局限性太强,必须保证机械手的前3个节点的封闭形式解在几何上存在;数值迭代法受初始值影响,容易出现迭代不收敛。神经网络能通过已知的数据来学习并逼近任何非线性函数,收敛速度快,精度高。近年来,运用神经网络进行6R机器人逆运动学求解开辟了一条新途径[6-7]。但运用该方法求解时普遍只是分析神经网络的结构,而忽略了训练样本对于神经网络输出精度的影响。
周毅等[8]指出对于网络学习样本的选择进行解释或说明的不多,对网络样本的选择还缺少一个统一的认识,不同的人会有不同的选择方式,其结果也就会出现差异。韩兴国等[9-10]指出训练样本的选择能够影响神经网络的学习和泛化能力,从而影响最终的求解精度,其通过模糊聚类理论,将整个机器人工作范围进行划分,然后寻求每一个工作区域的聚类中心,并以此为基础进行样本优选。最终选取8 000个点作为训练网络,得到了较好的结果。在另外一些文献中则未进行样本的择优选取,文献[6]中是在一定范围内选取600个样本点,文献[7]中则采用随机法选取700个样本点。均未明确指出训练样本质量问题。
利用神经网络求解机器人逆解过程中,为了规避复杂的样本优选工作,提出一种将代数法与神经网络相结合的方法,将神经网络得到的泛化能力强的关节角度作为解析解,然后直接代入到解析方程中进行其余关节的求解。这种方法结合了神经网络求解速度快和代数法精度高的优点。可以在不过分考虑样本优良的情况下,利用神经网络快速求解机器人运动逆解,并用代数法保证其精度,弥补样本可能带来的误差。相对于纯解析法,避免了多解情况,在一定程度上简化了计算过程。
1 6R机器人运动学及代数解法
6R机器人简化模型如图1所示,其运动副均为转动副,前3个关节用来确定机器人末端的空间位置,后3关节用来确定末端姿态。一般6R机器人的其后3个相邻关节轴相交于一点,满足Pieper准则,可以通过代数法求得其封闭解。
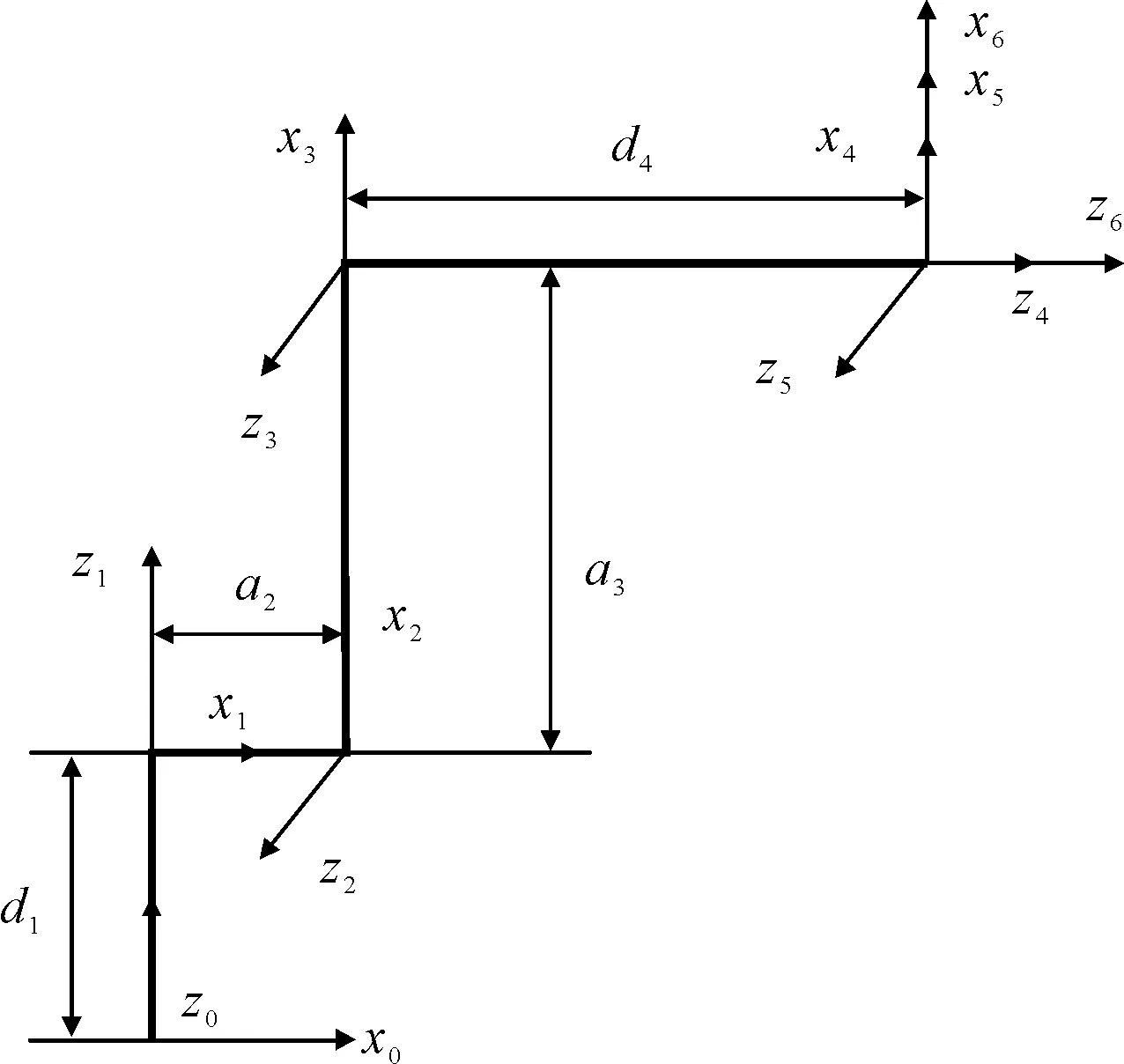
图1 6R机器人简化模型
代数解法首先要为6R机器人的每一连杆建立一个坐标系,确定D-H参数,并用齐次变换矩阵来描述这些坐标系间的相对位置和姿态,以获得末端执行器相对于基坐标系的齐次变换矩阵,求得机器人的运动方程。一般6R机器人的结构如图1所示(具体的型号可能在关节位置上有所变化),其中每个连杆两端关节的轴线方向为zi,相连关节轴线的公垂线的距离为ai,称为连杆长度;相连公垂线的距离为di,称为两连杆距离;上一轴线相对于下一轴线需要旋转的角度为αi,称为两连杆扭角;相连连杆之间的夹角为θi,称为连杆夹角。其对应的D-H参数如表1所示。

表1 D-H参数表
根据Craig参考坐标系建立约定,坐标系[i-1]到坐标系[i]的齐次变换矩阵为:
(1)
式中:sθi=sinθi;cθi=cosθi;sαi=sinαi;cαi=cosαi。根据文献[2],6R机器人末端关节坐标系相对于基础坐标系的坐标转换矩阵为:
0T6=0T11T22T33T44T55T6
(2)
根据式(2)可求出0T6,其表示基座到机器人末端的转换矩阵。
(3)
式中:RN为从机器人末端姿态;PN为机器人末端位置,RTH为机器人末端位姿。
nx=s6(s1c4-c1s4(c2c3-s2s3))+c6·
(c5(s1s4+c1c4(c2c3-s2s3))-s5c1(c2s3+c3s2))
(4)
ny=-s6(c1c4-s1s4(s2s3-c2c3))-c6·
(c5(c1s4-s1c4(s2s3-c2c3))-c5s1(c2s3+c3s2))
(5)
nz=-s23s4s6-c6(c23s5+s23c4c5)
(6)
ox=c6(s1c4-c1s4(c2c3-s2s3))-s6·
(c5(s1s4+c1c4(c2c3-s2s3))-s5c1(c2s3+c3s2))
(7)
oy=s6(c5(c1s4+s1c4(s2s3-c2c3))+
s1s5(c2s3+c3s2))-
c6(c1c4-s1s4(s2s3-c2c3))
(8)
oz=-s6(c23s5+s23c4c5)-s23c6s4
(9)
ax=s5(s1s4+c1c4(c2c3-s2s3))+
c1c5(c2s3+c3s2)
(10)
ay=c5(c2s1s3+c3s2s4)-
s5(c1s4+s1c4(s2s3-c2c3))
(11)
az=-c23c5+s23c4s5
(12)
px=c1(a2+d4s23+a3c2)
(13)
py=s1(a2+d4s23+a3c2)
(14)
pz=d1-d4c23+a3s2
(15)
式中:si=sinθi;ci=cosθi;sij=sin(θi+θj);cij=cos(θi+θj)

根据矩阵对应元素相等可求出θ1,将求得的θ1作为已知解,利用同样的办法可以求得其余解。一般前3关节用矩阵第4列元素对应相等求解,而后3关节则用前3列元素对应相等求解。
在求解过程中,已知0Tn的数值,求解θ1,θ2,…,θ6的所有可能解通常是一个多解耦合、高维度、非线性问题,求解复杂且不易求出,因此考虑使用RBF神经网络进行逼近。通过将各关节转角和机器人末端位姿作为训练样本的输出输入,不断训练RBF神经网络,使其逼近各关节转角和机器人末端位姿之间的变换矩阵关系,训练好的神经网络收到下一个位姿输入时,就能计算出各关节的转角,从而达到计算机器人逆解的目的。
在具体的机器人求解过程中输入为式(3)中的姿态RN和位置PN。共有12个变量,作为RBF模型的输入变量太多,会造成网络结构复杂,考虑将位姿矩阵转换为欧拉角,减少输入量。设定姿态RN按z-y-z轴的旋转顺序进行欧拉变换获得,末端姿态RN中的9个变量可以用欧拉角α,β,γ表示。根据坐标转换原理,求得机器人末端姿态RN。
α=atan2(ay,ax)
(16)
β=atan2(axcosα+aysinα,az)
(17)
γ=atan2(-nxsinα+nycosα,oycosα-oxsinα)
(18)
将Px,Py,Pz,α,β,γ作为RBF模型的输入变量。
2 RBF及代数法相结合的逆解预测模型
2.1 RBF神经网络模型
径向基网络(RBF)是一种用于函数逼近和模式识别的神经网络结构,其实质是给定一定样本之后,RBF神经网络寻找一组最优的径向基函数的节点中心W1和一组最优的输出权值W2,使RBF神经网络能够逼近样本输入与输出之间的关系,从而通过逼近的函数预测输出值在给定精度下最大限度地接近于实际输出。
径向基网络结构主要分为3层,第一层为输入层,节点个数等于输入维数;第二层为隐含层,节点个数视问题的复杂度而定;第三层为输出层,节点个数等于输出数据维数,其结构如图2所示。
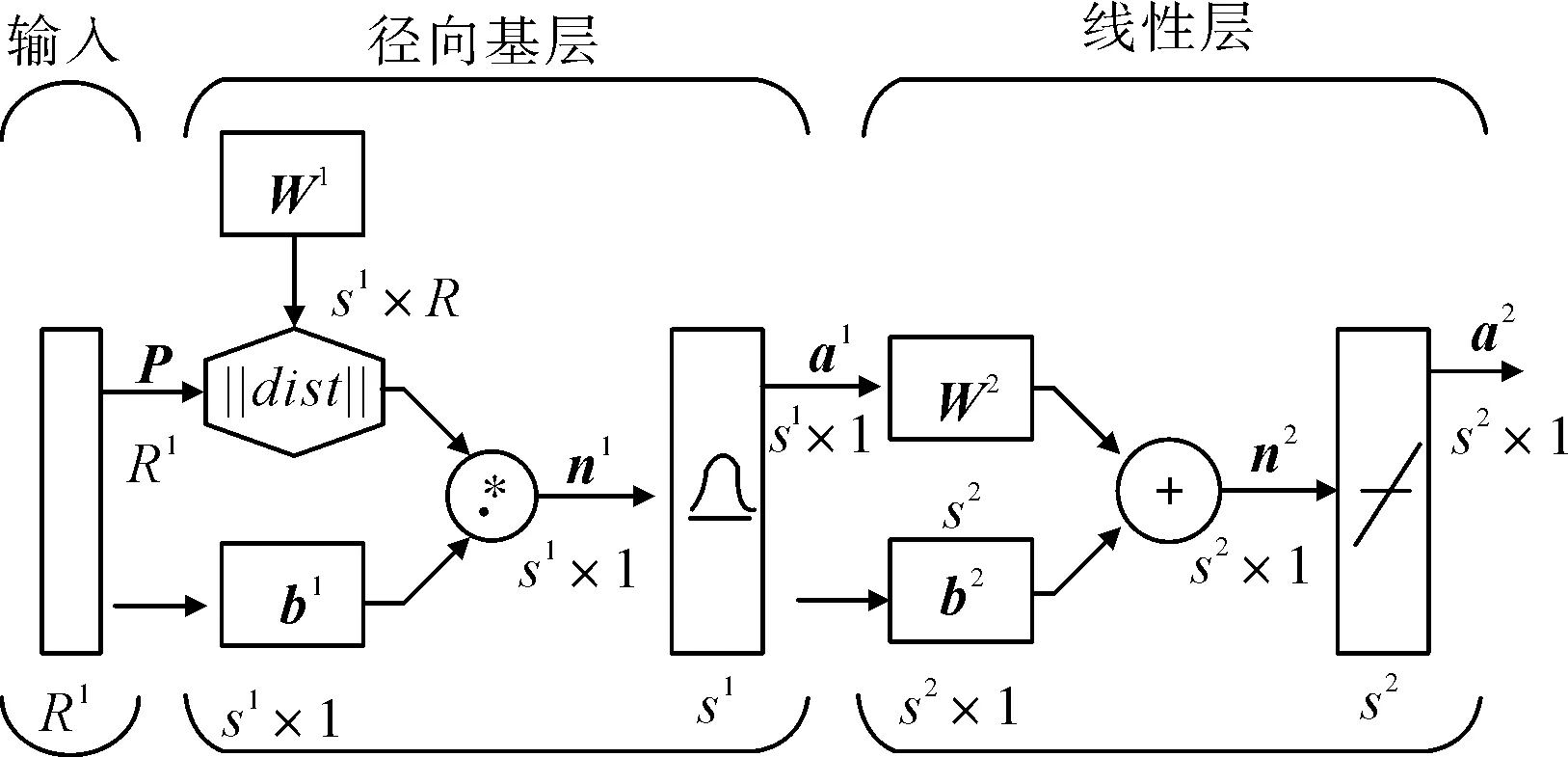
图2 RBF神经网络结构
径向基神经网络的激活函数是以输入向量和权值向量之间的距离‖dist‖作为自变量的。其中:
‖dist‖=‖P-iW1‖
(19)
第一层神经元i的净输入为:
(20)
RBF神经网络中有几种不同类型的传输函数,在此,考虑在神经网络中经常使用的高斯函数,其定义如下:
a1=e-n2
(21)
当使用高斯函数时,偏置值与标准差之间具有如下的关系:
(22)
得到的径向基输出为:
a1=radbas(‖P-W1‖b1)
(23)
RBF网络的第二层是一个标准线性层:
a2=W2a1+b2
(24)
即为输出与输入的关系:
(25)
式中:P为输入,大小为R1×1矩阵;radbas()为高斯函数;b1为偏置值,大小为S1×1矩阵;W1为径向基层的权值,大小为S1×R矩阵;a1为径向基层的输出,大小为S1×1矩阵;W2为线性层的权值,大小为S2×S1矩阵;a2为最终的输出,大小为S2×1。
2.2 样本参数归一化处理
数据归一化处理是将所有数据转化为0~1之间的数,其目的是取消各维数据间数量级差别,避免在计算过程中发生数据溢出的现象,归一化处理公式为:
(26)
式中:z为归一化前参数;zmin为参数最小值;zmax为参数最大值;z′为归一化后的参数。
在式(16)~式(18)中获得的位姿参数和关节角θ经过式(26)归一化处理后分别作为RBF的输入和输出参数,即输入参数P=[P′x,P′y,P′z,α′,β′,γ′]T,输出参数a2=[θ′1,θ′2,θ′3,θ′4,θ′5,θ′6]T,建立基于RBF神经网络的6输入6输出的逆运动学求解预测模型。
用该预测模型计算出的关节角需要进行反归一化处理:
θi=θimin+θ′i(θimax-θimin)i=1,2,…,6
(27)
式中:θ′i'为经过归一化处理后的预测输出关节角。
2.3 代数法和神经网络相结合
在一般的RBF神经网络6R机器人逆运动学求解中,普遍分析的是神经网络的结构,忽略了训练样本对于神经网络输出精度的影响。选点常见的方式是在每个关节的上下限范围(θdown,θup) 中随机选取N个训练样本点和n个测试样本点,利用这些点进行神经网络的训练和测试,计算得到相应的θ1,θ2,…,θ6。但不同的关节对于样本点的敏感性不一样,神经网络所建立的各个关节预测模型在不同的关节上其稳定性也会有所差异。
为了提高不稳定的关节预测模型的精度,将代数法融入到神经网络中,通过神经网络计算得到的θ1,θ2,…,θ6,将与预期的精度偏差较大的一个关节或多个关节解θi(i=1,2,…,6)舍去,将其余的解θj(j=1,i-1,i+1,…,6)作为已知解,再利用代数法反求出θi。
将代数法和神经网络相结合的目的是利用神经网络来简化机器人逆解的计算过程,利用代数法的精度来控制神经网络样本点所可能带来的误差,简化了样本点的选取过程,保证了神经网络求解的精度,避免代数法的非线性解耦,达到快速、精确求解机器人逆解的目的。
3 仿真分析
3.1 仿真模型的建立
以ABB IRB140作为仿真分析模型,该机器人属于6R机器人,其结构示意图如图3所示。

图3 ABB IRB140机器人本体参数
其中对应的D-H参数为:d1=352 mm,a2=70 mm,a3=360 mm,d4=380 mm。
利用MATLAB机器人工具箱,建立ABB IRB140模型如图4所示。

图4 MATLAB IRB140机器人模型
3.2 仿真计算
通过式(16)~式(18)可以求得RBF神经网络的输入。
使用随机选取方法选取样本点。在选取样本点时,将θ1,θ2,…,θ6的取值范围都限定在(0°,28°)内,随机选取1 000个样本点。仿真结果如图5所示。计算得到的各关节转角与真值之间的平均误差如表2所示。
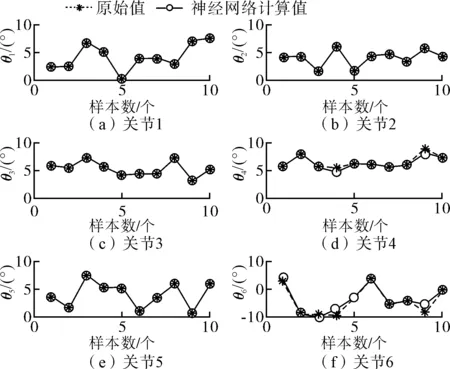
图5 RBF神经网络仿真结果一
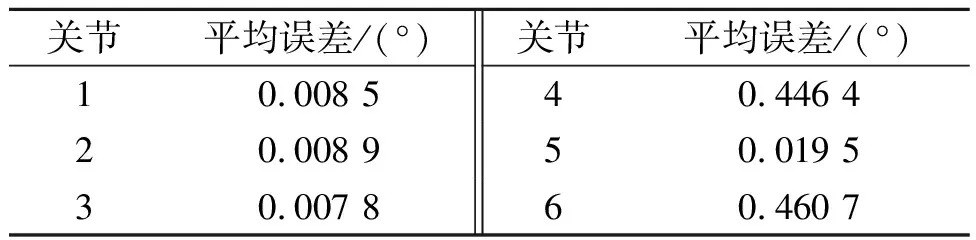
关节平均误差/(°)关节平均误差/(°)10.008 540.446 420.008 950.019 530.007 860.460 7
为了说明训练点的选取对于精度的影响,通过改变各个角度的取值范围,将θ1,θ2,…,θ6,的取值范围分别限定在(0°,56°),(0°,56°),(0°,56°),(0°,28°),(0°,28°),(0°,28°)内,随机选取1 000个样本点。仿真结果如下图6所示。计算得到的各关节转角与真值之间的平均误差如表3所示。

图6 RBF神经网络仿真结果二
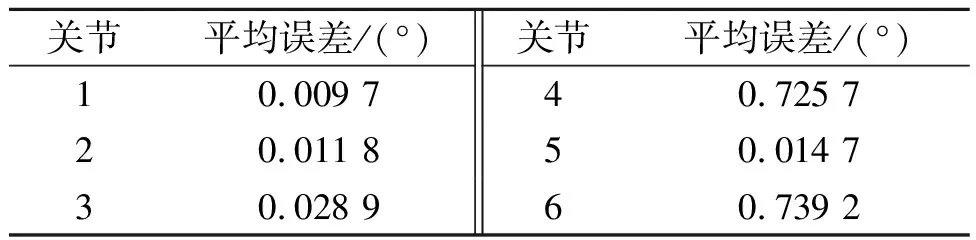
关节平均误差/(°)关节平均误差/(°)10.009 740.725 720.011 850.014 730.028 960.739 2
通过训练好的网络进行测试时,在训练范围内按照随机选取10个点进行测试,从图6可知,即使前3关节的角度取值范围变大,即训练样本的相对密度减小时,其泛化能力依然很好,而第四关节和第六关节泛化能力相对较差。为了解决神经网络在后3关节的泛化能力相对较差的情况,提出将神经网络法和代数法相结合的方法。
使用第二组训练结果,即θ1,θ2,…,θ6的取值范围分别限定在(0°,56°),(0°,56°),(0°,56°),(0°,28°),(0°,28°),(0°,28°)内时,通过训练RBF神经网络获得的θ1,θ2,θ3,θ5数值,利用代数法求得第四,第六关节的转动量。
用逆变化左乘式(3)的两边得:
(28)
令式(28)两端的元素(1,3)和(3,3)对应相等可得:
axc23c1+ayc23s1+a2s23=c4s5
(29)
axs1-ayc1=s4s5
(30)
根据三角变换可得:
θ4=atan2(s4,c4)
(31)
同理可得:
θ6=atan2(s6,c6)
(32)
因为其它角度都已知,不存在解耦的过程,极大地简化了计算过程。利用RBF神经网络获得的θ1,θ2,θ3,θ5数值及式(31),式(32)求得的结果如图7所示。
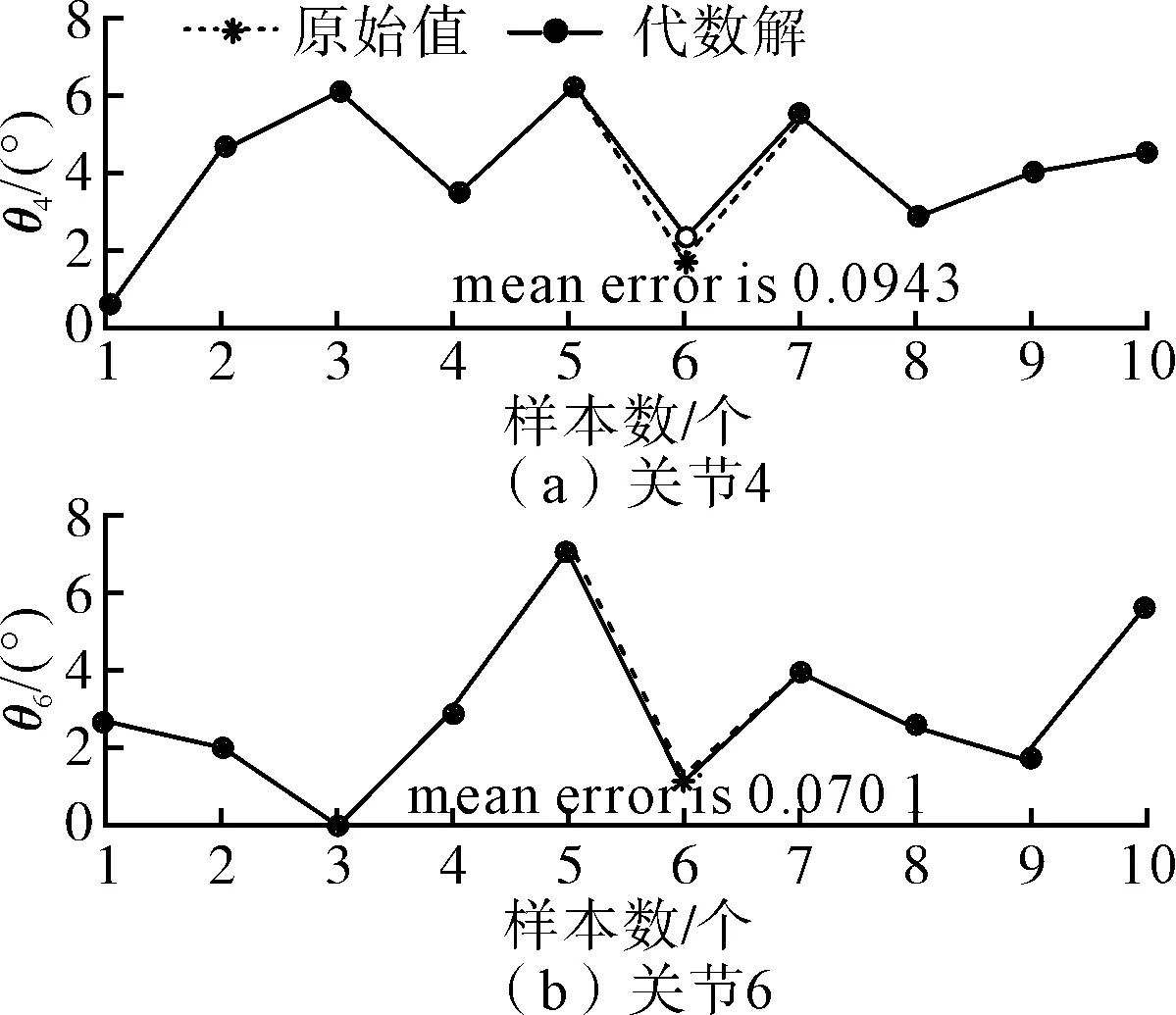
图7 代数解与真值之间的误差
用代数法计算得到的平均误差分别为0.094 3°和0.070 1°,相比于直接用神经网络得到平均误差0.725 7°和0.739 2°来说精度提升了一个量级。
4 结论
(1)提出了一种基于RBF神经网络与代数法的6R机器人逆运动求解方法,该方法避免了未经优化选取的样本造成网络泛化能力相对较差的情况,同时也省去了样本优化的的繁琐过程。另一方面在一定程度上简化了代数法的解耦与选优的过程,是一种结合神经网络与代数法优点的方法。在简化求解过程中又保证了解的精确性。
(2)基于RBF神经网络与代数法的预测模型能广泛应用于其他一般6R机器人,可获得较高的逆解精度。
