真空管道磁悬浮列车支承设计与特性分析

熊振宇，胡业发，冉少林，陈昌皓

(1.武汉理工大学 机电工程学院，湖北 武汉 430070；2.湖北省磁悬浮工程技术研究中心，湖北 武汉 430070)

利用电磁力悬浮、导向和驱动的上海磁悬浮列车速度可达430 km/h，比目前任何商用列车更快、更安静[1]。但是对于地面交通运输工具，受限于地表稠密的大气层，随着速度的提高，特别是速度超过300 km/h，强大的气动阻力和气动噪音使速度难以继续提高[2]。虽然磁悬浮列车借助于电磁力将车辆悬浮在轨道上方，消除了车轮与轨道的摩擦，但其速度仍受限于大气环境的影响。为解决以上问题，可在真空管道中运行磁悬浮列车，稀薄的大气环境极大地降低了空气阻力，目前主要的悬浮方案有美国的Hyperloop、ETT和瑞士的Swissmetro等[3-4]。

埃隆·马斯克2013年提出的超级环路列车Hyperloop alpha采用气悬浮，其后Hyperloop采用永磁电动悬浮，其悬浮支承原理与Inductrack和Magplane相似，都属于电动悬浮(electrodynamic suspension，EDS)，由导体和永磁体之间相对运动产生的排斥力实现悬浮。EDS具有悬浮间隙大、能耗低和结构简单等优点，存在的主要问题有低速需要辅助轮支撑，是一个临界稳定系统，目前并没有实现商业化应用[5-8]。

瑞士地铁Swissmetro和德国Transrapid都属于电磁悬浮(electromagnetic suspension，EMS)，利用电磁吸力抵消系统的重力。EMS技术是目前磁悬浮列车悬浮技术中最成熟的，但其存在悬浮间隙小、控制难度大和成本高等问题[9]。ETT和西南交通大学利用高温超导材料的磁通钉扎来实现悬浮和导向，其悬浮和导向具有自稳定性，无需主动控制系统，但需要液氮冷却，且尚处于实验室研究阶段[10-11]。

针对上述问题，设计一种采用永磁电动悬浮和电磁悬浮混合的磁悬浮支承结构，永磁电动悬浮提供主要的悬浮和导向力，电磁悬浮用作辅助支承来提高支承系统的稳定性。建立承载力计算模型，用解析法分析承载力的特性。为了保证结构设计的合理性，在进行理论计算的同时，利用ANSYS Maxwell软件对磁场进行仿真，研究设计参数对磁场和支承特性的影响，比较两者的误差，验证支承方案的可行性。

1 结构和模型

以真空管道磁悬浮列车为应用背景，提出一种采用永磁EDS&EMS混合磁悬浮支承系统的悬浮支承方案，其结构示意图如图1所示。永磁电动悬浮由固定在车体上的永磁Halbach阵列和固定在管道上的感应板组成，倾斜布置用来提供列车所需的主要悬浮与导向力。电磁悬浮由固定在车体上的电磁铁和固定在管道上的轨道组成。电磁悬浮可以增加系统的阻尼，提高稳定性。低速时，用辅助轮支承并用电磁悬浮卸荷。

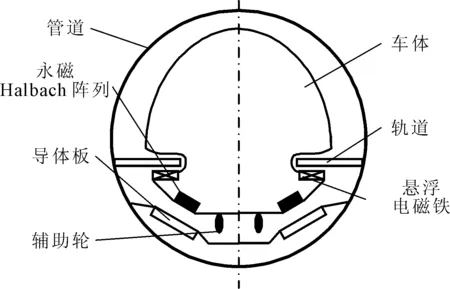
图1 混合磁悬浮支承结构示意图

1.1 永磁电动悬浮模型

电动悬浮主要有两种形式，一种是利用超导线圈和短路线圈的相对运动产生斥力实现悬浮，日本超导磁悬浮列车采用这种形式。另一种是通过永磁体和短路导体的相对运动产生斥力，高磁场强度的材料和Halbach阵列用来解决悬浮力不足的问题，美国的Inductrack和Hyperloop等均采用这种形式[12-14]。

永磁电动悬浮模型如图2所示。当永磁阵列与导体板存在相对运动时，会使导体中产生随永磁阵列运动的涡流，涡流磁场与永磁阵列磁场相互作用产生悬浮力和阻碍两者相对运动的阻力。导体板上产生的涡流对悬浮力与磁阻力有直接的影响，进而影响整个系统的悬浮性能。主要的结构参数有永磁Halbach阵列和导体板的尺寸、材料和气隙。

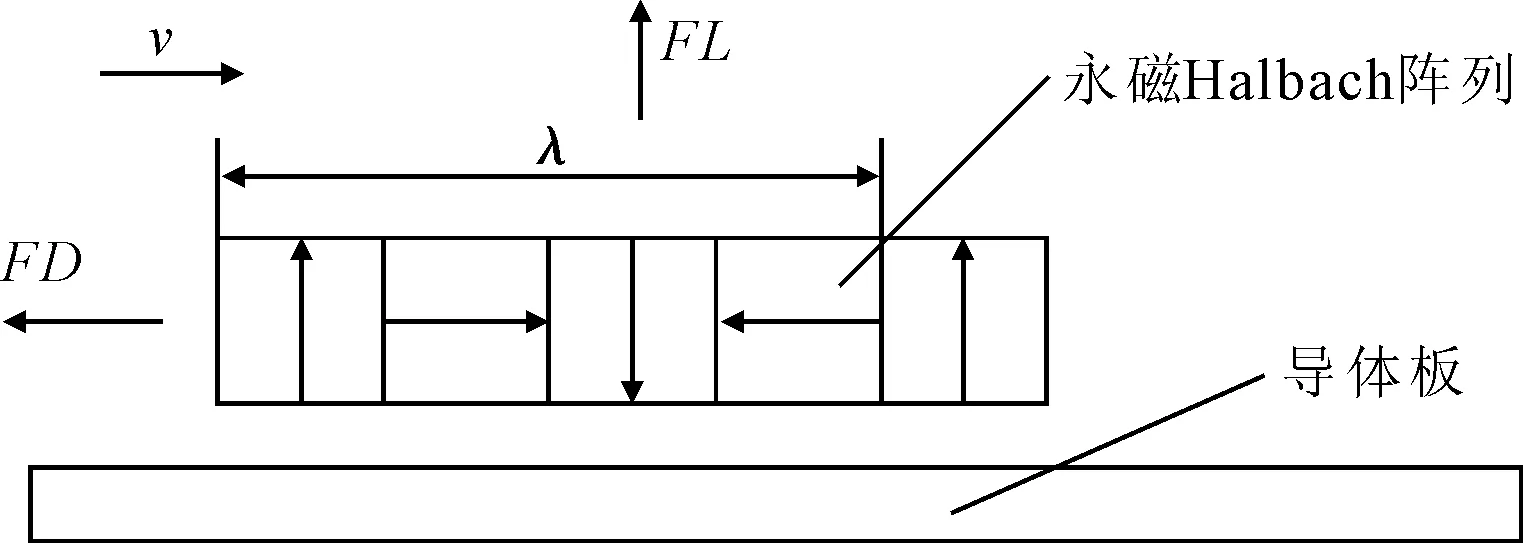
图2 永磁电动悬浮简化模型

Halbach阵列由多块相同磁化强度的永磁体模块组成，相邻永磁体的充磁方向按照一定的角度旋转，可以使磁场在阵列的一侧相互叠加，在另一侧相互抵消。因此，Halbach阵列能够使磁场能量集中在一侧，最大化利用磁场能。根据文献[12]，Halbach阵列的加强侧磁场的峰值强度Bd的计算公式为：

(1)

式中：Br为永磁体的剩磁；d为永磁体的厚度；M为一个波长的永磁体个数；k=2π/λ，λ为一个波长的长度。

永磁电动悬浮的最大悬浮力Fmax、悬浮力FL和磁阻力FD[12]计算公式如下：

(2)

(3)

(4)

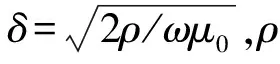
由上述公式可知，悬浮力与阵列的结构尺寸、气隙和相对速度有关，随着速度的增大渐渐逼近最大悬浮力；最大悬浮力与结构尺寸以及气隙有关，而与相对速度无关；系统的结构参数确定以后，悬浮力与磁阻力的比值与速度呈正相关。上述公式只能近似计算永磁电动悬浮的悬浮力和磁阻力，在前期设计起指导作用，还需通过有限元分析和实验来进一步验证。

1.2 电磁悬浮模型

电磁悬浮简化模型为U型或E型电磁铁，如图3所示。

图3 电磁悬浮简化模型

以电流密度来约束最大电流和导线直径，且线圈整齐排列，忽略漆包线漆层厚度的影响，则最大安匝数和发热功率不会随线径变化，最大安匝数Ni和发热功率P如下：

(5)

(6)

式中：dc为线圈直径为；S为线圈腔的面积；J为电流密度；i为线圈电流；R为线圈电阻；ρcu为铜的电阻率；lcu为每匝线圈的平均长度，其值与铁芯柱和线圈腔的尺寸有关；N为线圈匝数。

但在实际工程中，由于绕线等问题会存在差异，且线径小匝数多会使电阻和电感增大，不利于控制。在忽略漏磁通和边缘磁通、不考虑饱和等假设下，铁芯间的吸引力F可以通过以下方程近似计算：

(7)

(8)

式中：A0为气隙处的总磁极面积；B0为气隙处的磁通密度；le为铁芯磁路的平均长度；μe为铁芯的磁导率；Ae为磁芯的磁极面积；x2是动子和定子之间的气隙。

μe远大于μ0，因此磁通密度可用安匝数和气隙近似计算。气隙处的总磁极面积A0一般用磁芯的磁极面积Ae近似计算，但气隙增大后漏磁通和边缘磁通不可忽略，实际Ae应小于A0，上述公式计算的B0偏大，但由于铁芯相对磁导率远大于1，气隙增大对B0的影响小于对磁极面积A0的影响，最终呈现的结果是理论计算结果偏小。

2 建模与仿真

为了保证混合磁悬浮支承结构设计的合理性，利用ANSYS Maxwell有限元分析软件对永磁电动悬浮和电磁悬浮分别进行了磁场数值模拟仿真分析，以研究混合磁悬浮支承系统的设计参数对磁场及支承特性的影响。同时为了研究各参数对悬浮性能的影响，得到更加准确的仿真结果，在Maxwell中采用参数化建模。

2.1 二维瞬态磁场有限元分析

永磁电动悬浮的仿真模型如图4所示。永磁体材料为NdFe35，导体板为铝，其它部分都是真空。该仿真类型为二维瞬态磁场分析，应首先验证网格和时间步长的无关性。求解域和运动区间的网格对结果影响较小，阵列、导体板和气隙的网格都需要加密，时间步长设置应保证悬浮力时间曲线光滑且达到稳态。

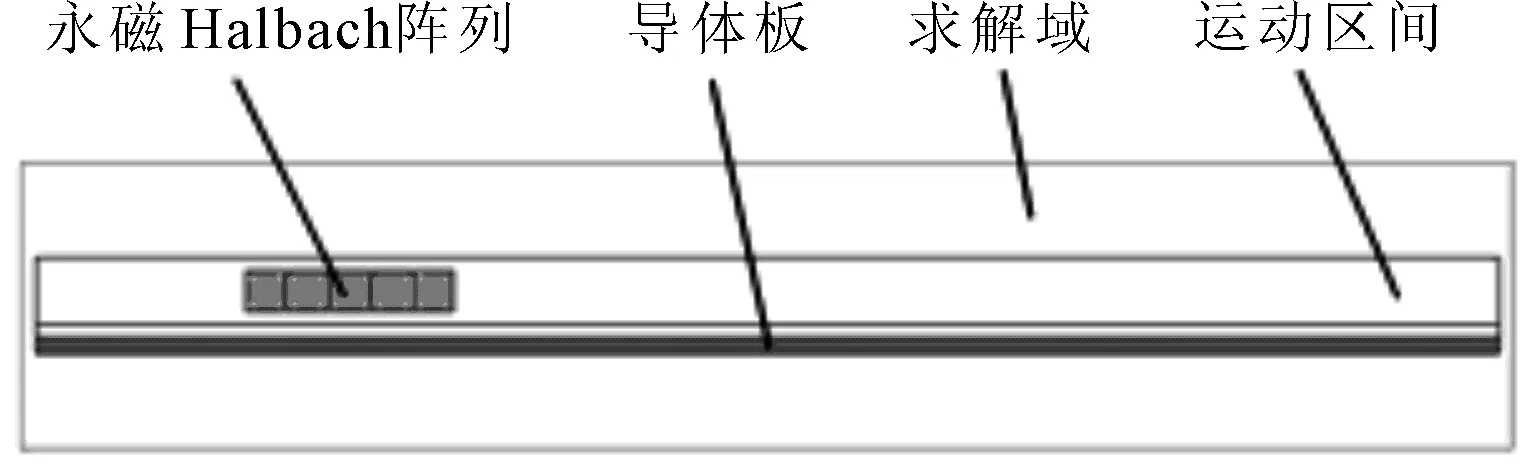
图4 永磁电动悬浮仿真模型

采用全参数化建模，即所有模型尺寸均用参数表示，另外还要考虑速度和仿真时间。为便于实验验证，永磁电动悬浮仿真的参数和初值如表1所示，由于是二维仿真，永磁体和导体板的宽度相同且都为Lz，在实际工程中导体板宽度大于永磁体。

表1 永磁电动悬浮参数

选用模块数为4的Halbach阵列，磁场方向可以通过建坐标系或改变材料属性中的充磁方向来实现。导体板的长度由速度、仿真时间和阵列的长度确定，阵列及其运动过程均要在运动区间内部。选取时间步长为1 ms，不同速度下的悬浮力时间曲线如图5所示。

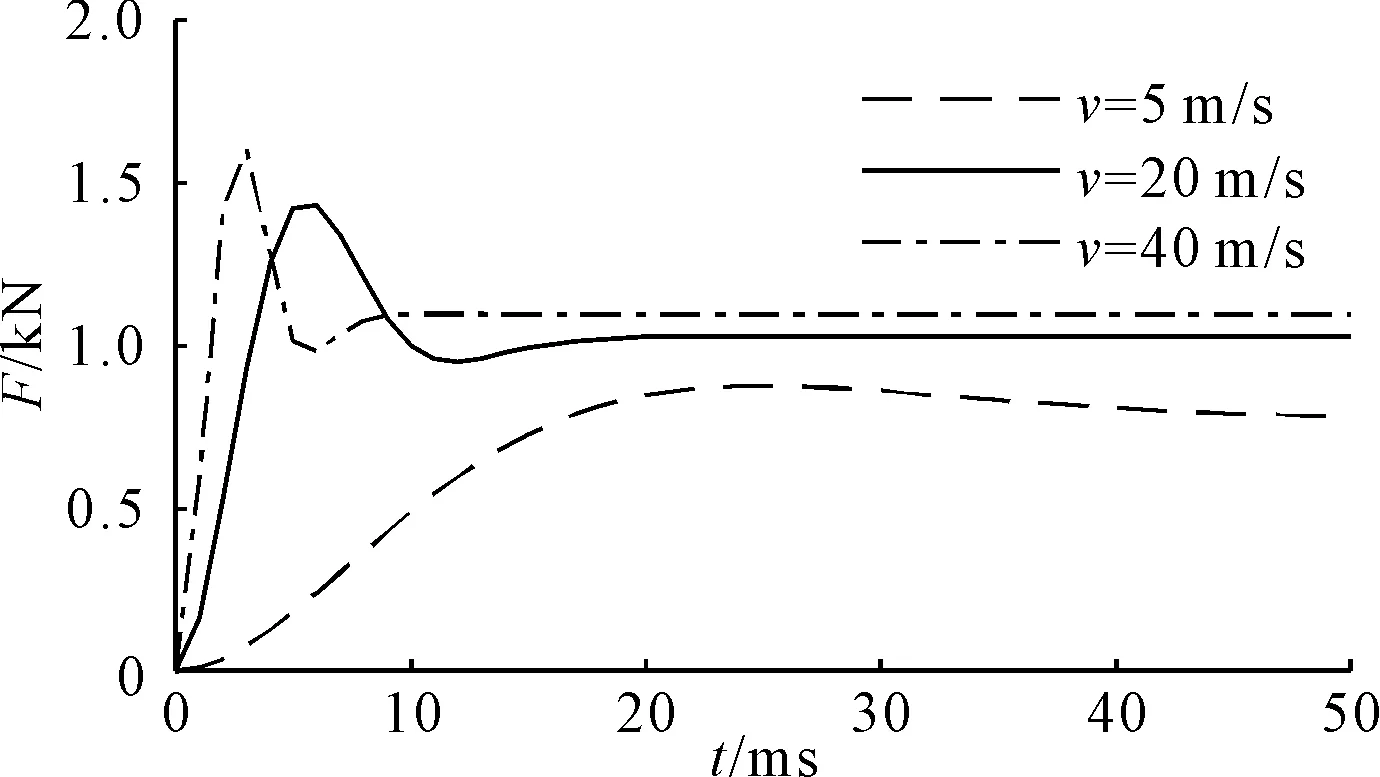
图5 不同速度下的悬浮力时间曲线

在相同的设置和时间步长下，求解不同速度时的悬浮力，每个时间步长内的位移随速度增大而增大。虽然设置的是匀速运动，但软件求解时会有加速过程，在本算例中1 ms后达到设定速度，如图6所示。由于加速过程的存在，图5中的悬浮力并不是一直稳定不变的，在一个时间步长的位移过大会影响加速过程的求解精度，从而影响达到稳定状态后的悬浮力大小，故悬浮力时间曲线的质量随速度增大而下降，在本算例中速度超过20 m/s后为明显的折线。

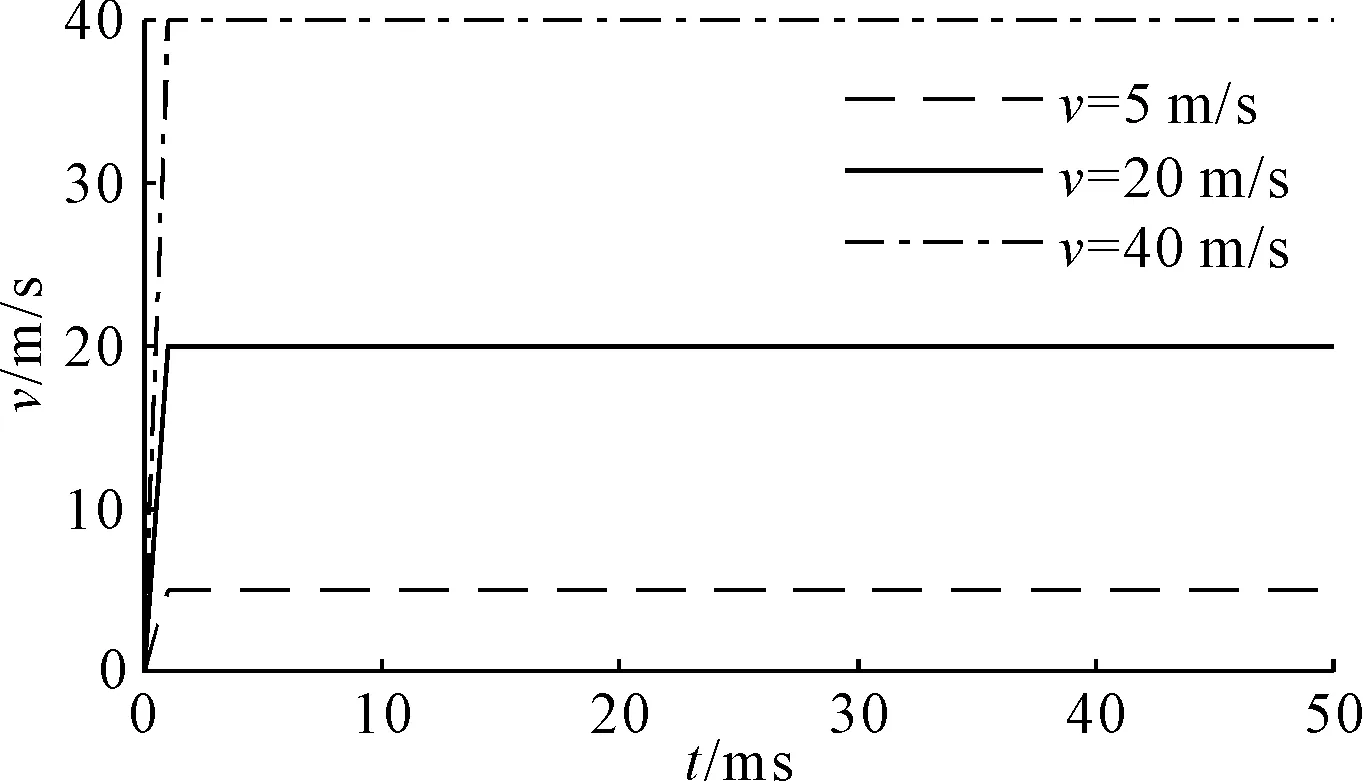
图6 速度时间曲线

高速时悬浮力很快达到稳定状态，而低速则需更多时间，同时高速相比于低速需要更小的时间步长。因此，保证不同速度下有相同的步数，可以得到光滑的曲线，减小仿真误差，通过调整参数，最终确定的仿真时间t和导体板的长度dx为：

(9)

(10)

式中：n为仿真的步数，取n=150。式(9)可保证每个时间步长的位移是相等的，而图5的结果是由于随着速度增大，每个时间步长的位移在增大，最终导致误差变大。导体板的长度由两部分构成，整个运动过程的位移加上前后预留的长度。参数化模型改进后速度为5 m/s和40 m/s的悬浮力时间曲线如图7所示。

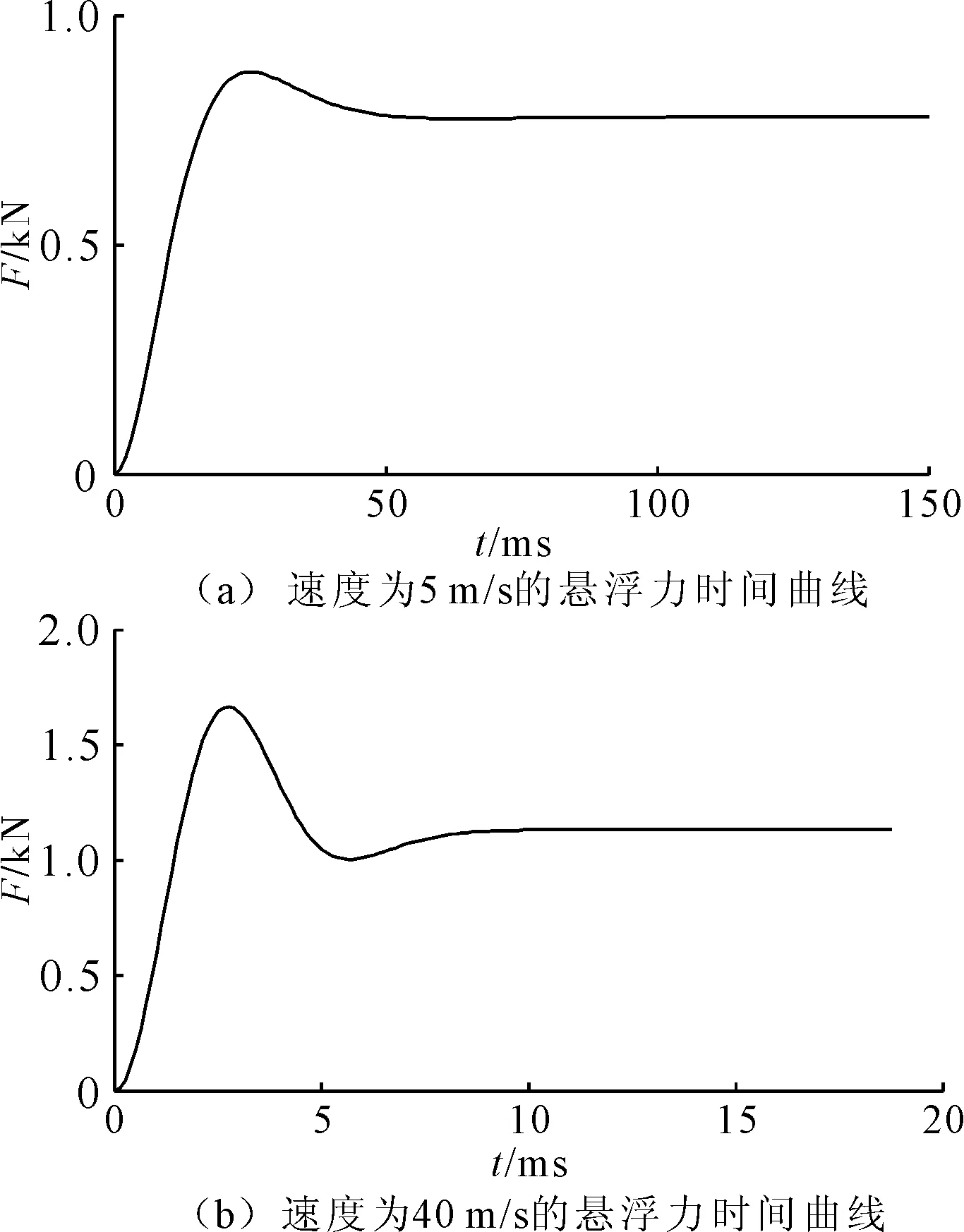
图7 改进后的悬浮力时间曲线

改进后的参数化模型，速度为40 m/s的悬浮力提高了3.4%，速度为5 m/s的悬浮力几乎没有变化，这是由于50 ms刚好在其平衡状态附近，速度更低时会有较大误差，速度为2 m/s时悬浮力相差4.7%，速度为1 m/s时悬浮力相差29.5%，改进后仿真时间根据速度不同有所改变，低速时也能达到稳态，高速时减少仿真时间。根据图7可知，悬浮力稳定后才是该速度下的有效值，取不同时刻的平均值或均方差都会增大误差。

图8是不同时刻二维瞬态分析中的磁通密度云图。当t=0时，反映的是Halbach阵列磁场单边加强的特性，由于相对运动，产生涡流磁场，速度稳定后磁场也达到一个稳定的状态。

图8 初始参数下不同时刻的磁场分布

2.2 二维静态磁场有限元分析

电磁悬浮的仿真在二维静态磁场中进行即可，其结构参数如表2所示。铁芯的结构尺寸是相互关联的，这与磁通有关，即尺寸要保证磁通密度相同，否则会造成浪费，某区域磁饱和后会限制磁通。根据承载力和材料的饱和磁化强度确定磁极面积，然后根据选定的气隙确定安匝数，安匝数可以求出线圈腔面积，线径与最大电流有关而不会影响安匝数的大小。在仿真时不需要设置匝数和电流大小，直接给定安匝数即可。

图9为不同气隙下的磁场分布，从图9中可知气隙小的情况漏磁通和边缘磁通可以忽略不计。随着气隙的增大，漏磁通和边缘磁通对计算的影响越来越大。但对于磁悬浮列车，其结构尺寸较大，10 mm气隙时漏磁通的影响并没有图9那么大。

表2 电磁悬浮参数

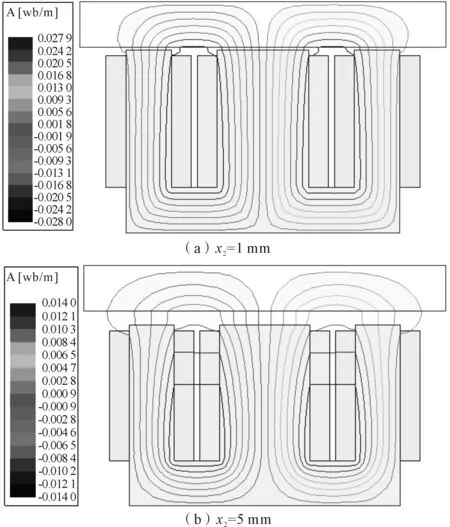
图9 不同气隙下的磁场分布

3 结果分析

参数化建模后利用ANSYS Maxwell参数扫描可以得到各参数与悬浮力的关系，与理论计算的结果比较，分析承载特性和误差。为便于后期的实验验证，所选择的计算参数并不是实际列车的承载力要求。

永磁电动悬浮的结果并不能在Maxwell用内置函数得到，这是由于不同速度设置了不同的仿真时间，需要将悬浮力时间曲线的稳定值提取出来，永磁电动悬浮力速度曲线如图10所示。此外观察每个悬浮力时间曲线是否达到稳态和是否平滑也有利于提高精度。

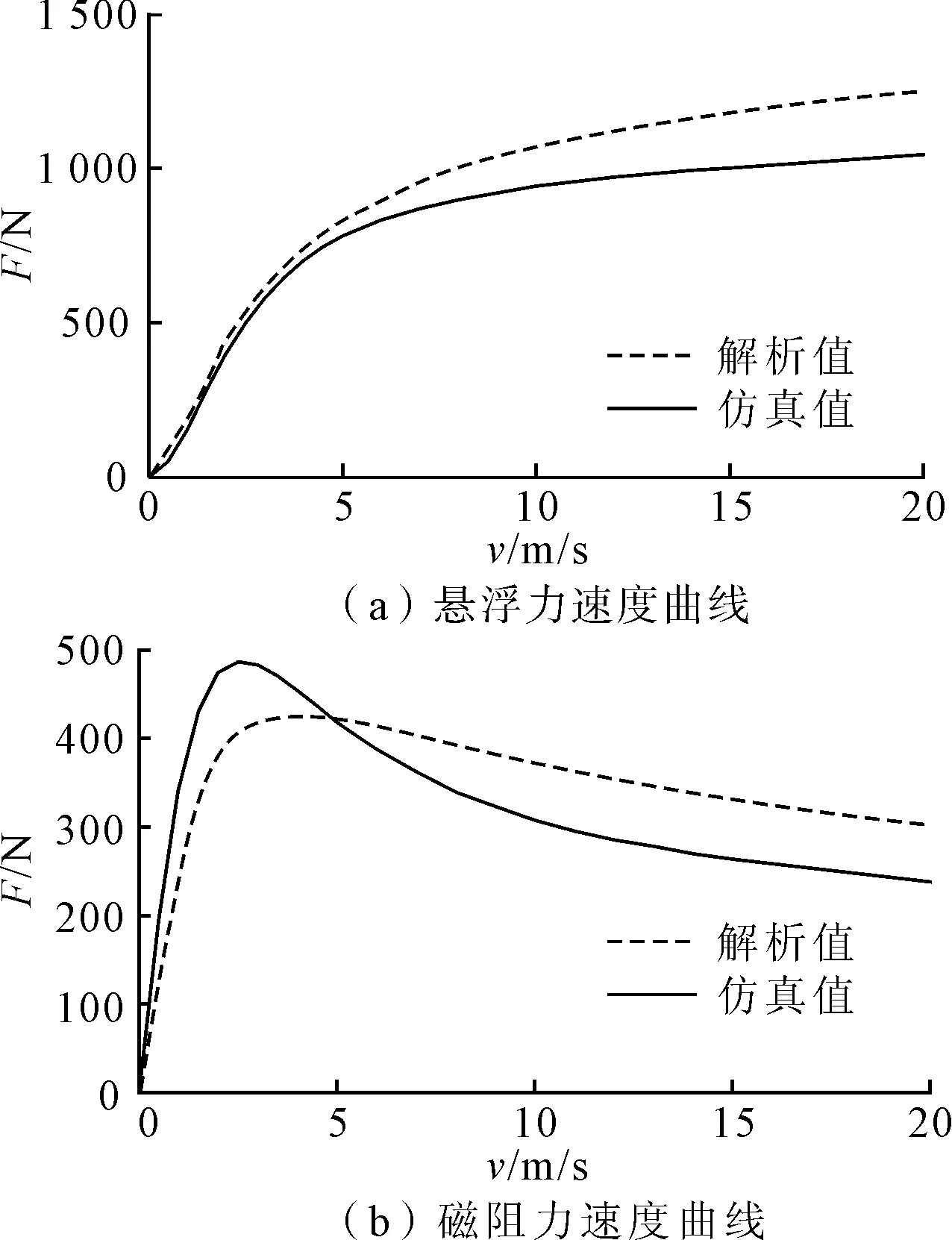
图10 永磁电动悬浮力速度曲线

从图10可知解析值和有限元仿真的结果是吻合的，仿真值小于解析值，且在高速时由于材料属性的限制，两者的差距变大，5 m/s时悬浮力误差只有7.3%，而20 m/s时误差达到19.5%。悬浮力随速度增大而增大但是增大的速率逐渐减小，而磁阻力是先增大后减小的。在实际应用时，列车应工作在合理的速度区间以保证较大的悬浮力和较小的阻力。

对于电磁悬浮，其电磁悬浮力气隙曲线如图11所示，从图11可知,两种方法得到的气隙曲线是一致的。气隙大于3 mm后，解析值小于仿真值，这是由于气隙小时漏磁通和边缘磁通的影响较小，且没有考虑磁饱和的问题。用表2的数据和式(8)计算得到的气隙处磁通密度为0.377 T，仿真得到的磁通密度为0.426 T和0.322 T，由于漏磁铁的影响，中心铁柱的磁通密度高于两侧。

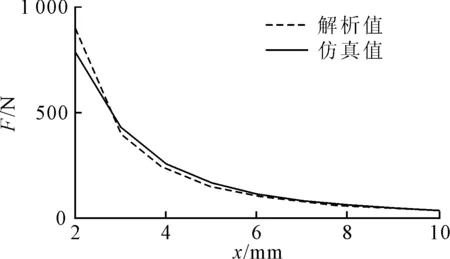
图11 电磁悬浮力气隙曲线

4 结论

以真空管道磁悬浮列车为应用背景，采用永磁电动悬浮和电磁悬浮混合支承。通过理论分析、参数化建模和仿真，研究了力与速度的关系，悬浮力随速度增大而增大但增大的速率在减小，磁阻力先增后减。保证瞬态分析每个时间步长的位移相同，可以提高仿真精度和效率。磁阻力达到最大值时，解析值和仿真的误差低于10%；速度继续增大后，误差增大到20%左右。电磁悬浮提高悬浮的稳定性，随着气隙的增大，边缘效应使实际磁极面积增大，导致解析值误差变大，漏磁导致中间铁柱气隙的磁通密度大于两侧，铁芯在磁饱和前仿真和解析值的误差小于10%。