基于ADAMS的差速器建模与运动仿真分析
2019-10-09任志立李浙昆
任志立 李浙昆

摘 要: 差速器在汽车直线行驶和转弯行驶中有重要的作用,差速器内结构复杂,机构较多,包括减速机构、差动轮系机构、传动半轴机构等,故差速器内机构的运动特性十分复杂。车辆上较为常用的是对称式锥齿轮差速器,其各机构的运动特性在各型减速器中较有代表性。首先分析差速器的差速原理,采用adams建立对称式锥齿轮差速器的虚拟样机三维实体模型,然后添加约束和驱动,应用虚拟样机运动仿真模块对该型差速器进行运动仿真。通过对运动仿真的结果进行分析,得出对称式锥齿轮差速器中各构件的运动特性,可以更深入的了解差速器的工作原理。
关键词: 差速器;adams;三维实体建模;运动仿真;运动特性
中图分类号: TP202 文献标识码: A DOI:10.3969/j.issn.1003-6970.2019.07.032
【Abstract】: Differential plays an important role in straight-line driving and cornering driving of automobiles. The internal structure of differential is complex and there are many mechanisms, including deceleration mechanism, differential gear train mechanism, transmission half-axle mechanism, etc. Therefore, the motion characteristics of the internal mechanism of differential are very complex. Symmetrical bevel gear differential is commonly used in vehicles, and the motion characteristics of each mechanism are representative among all types of reducers. Firstly, the differential principle is analyzed, and adams is used to establish a three-dimensional solid model of the virtual prototype of the symmetrical bevel gear differential. Then, constraints and drives are added, and the motion simulation module of the virtual prototype is used to simulate the motion of the differential. Through the analysis of the results of motion simulation, the motion characteristics of each component in the symmetrical bevel gear differential are obtained, and the working principle of the differential can be further understood.
【Key words】: Differential gear; adams; 3-D solid modeling; Motion simulation; motion characteristic
0 引言
驱动桥是车辆驱动系统中的重要组成部分,动力从发动机输出经过离合器、变速器、传动轴传动到驱动桥上,通过驱动桥内差速器的主减速器齿轮减速,然后通过差动轮将动力分配并传输到与车轮连接的左右两个半轴上,半轴带动车轮转动。故其中差速器的作用有两个,一是起减速作用,二是向两侧半轴分配扭矩。当车辆直线行驶时,受汽车两侧轮胎制造误差、胎压等因素影响,车辆轮胎周长存在微小差别,车辆两侧车轮长距离行驶相同距离时转过的圈数不相同,短距离行驶时车轮转过的圈
数基本相同。在车辆转弯时,内侧车轮的转速远小于外侧车轮的转速。若车辆不使用差速器由同一刚性驱动轴连接的两个车轮转速相同,但车轮需不同转速的功能却不能实现,车轮会出现滑动现像[1-4]。
1 差速器的组成和传动原理
1.1 差速器的組成
普通车辆上的差速器通常由传动轴、主动齿轮、从动齿轮(环型齿轮)、左半轴齿轮、右半轴齿轮、行星齿轮、行星轮架(差速器壳)、左右输出轴等零件构成。
1.2 差速器差速传动原理
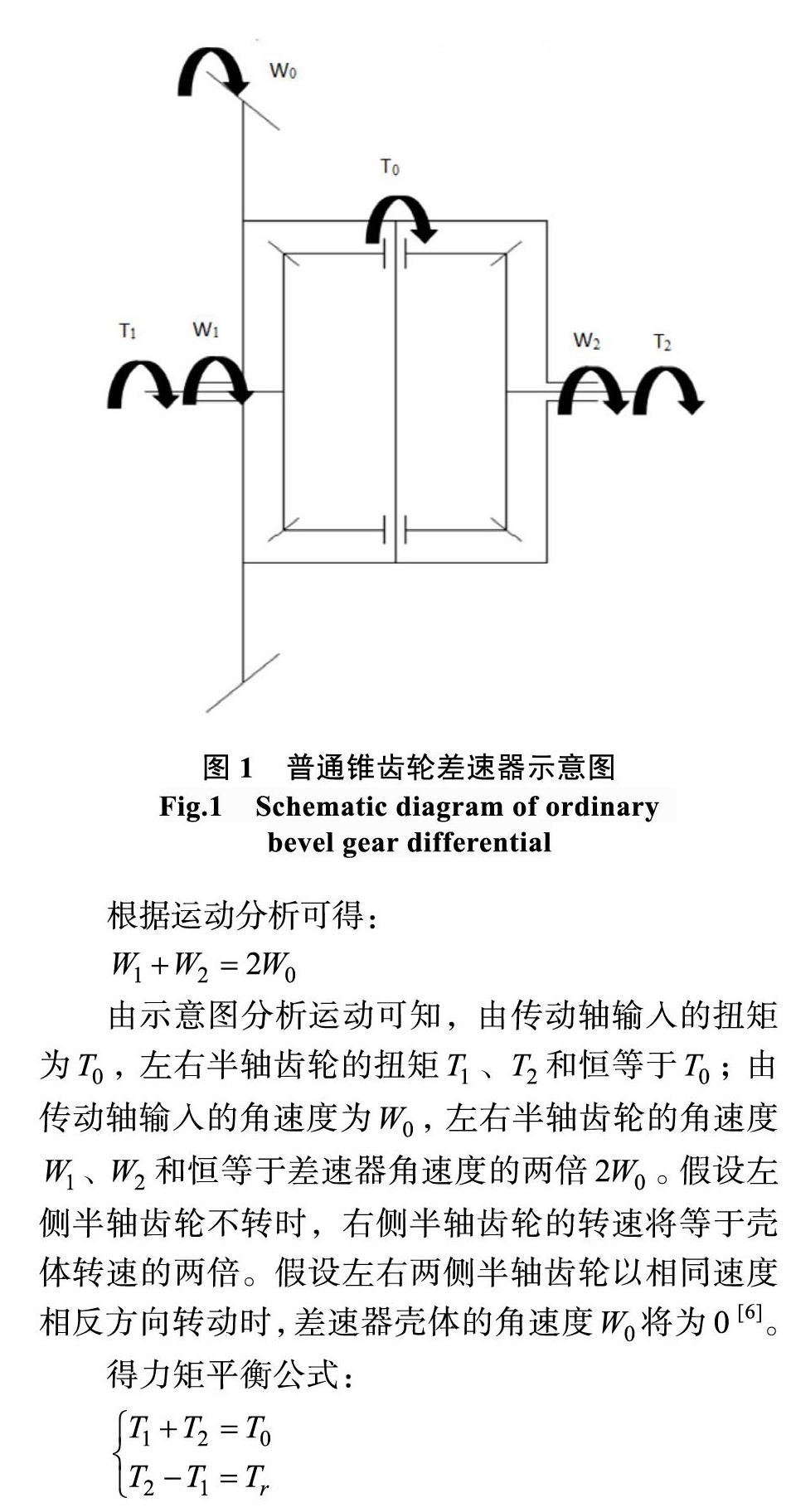
对称式锥齿轮差速器是较为常用的差速器,它具有结构简单、质量轻等优点,非常适合在轿车驱动桥上使用,而对称式锥齿轮差速器又分为普通锥齿轮式差速器、摩擦片式差速器和强制锁止式差速器等[5]。普通锥齿轮式差速器其示意图如图1所示。W0—差速器壳的角速度;W1、W2—左、右两半轴的角速度;T0—差速器壳接受的转矩;T1、T2—左、右两半轴对差速器的反转矩。
根据运动分析可得:
由示意图分析运动可知,由传动轴输入的扭矩为 ,左右半轴齿轮的扭矩 、 和恒等于 ;由传动轴输入的角速度为 ,左右半轴齿轮的角速度 、 和恒等于差速器角速度的两倍 。假设左侧半轴齿轮不转时,右侧半轴齿轮的转速将等于壳体转速的两倍。假设左右两侧半轴齿轮以相同速度相反方向转动时,差速器壳体的角速度 将为 [6]。
得力矩平衡公式:
2 对称式锥齿轮差速器的转矩分配
在对称式锥齿轮差速器中根据行星齿轮的转动形式不同,转矩分配分为两种形式。
(1)当车辆左右两个车轮受到的摩擦力相等时,行星齿轮只做公转运动不做自转运动。由主减速器输出的转矩 ,经差速器壳和行星齿轮传递给半轴齿轮,由于两个半轴齿轮分度圆半径和模数相等,因此左右两个半轴齿轮得到行星齿轮平均分配的扭矩 、 ,即:
(2)当车辆左右两个车轮受到的摩擦力不相等时,转矩更多传递到所受阻力较小的一端,行星齿轮同时做公转运动和自转运动。驱动桥内左侧半轴的转速不等于右侧半轴转速,由于两侧齿轮转速不同,故行星齿轮两侧会受到速度差产生的力,使行星齿轮绕自身轴线自转。当行星轮存在自转时行星轮轴和它配套的轴颈之间存在摩擦力,由摩擦力产生力矩。左右车轮的转矩差的内摩擦力矩 ,对左右半轴施加等大反向的作用力均衡转速不同的两个半轴的转矩[7]。
现在汽车上广泛应用的对称式锥齿轮差速器,其内部的行星轮轴和与它配套的轴颈之间存在摩擦力较小,因此无论左右半轴的转速是否相同,减速器主减速齿轮分配给左右半轴的扭矩都看作是均匀的[8]。
3 基于adams的差速器建模
3.1 差速器模型的建立
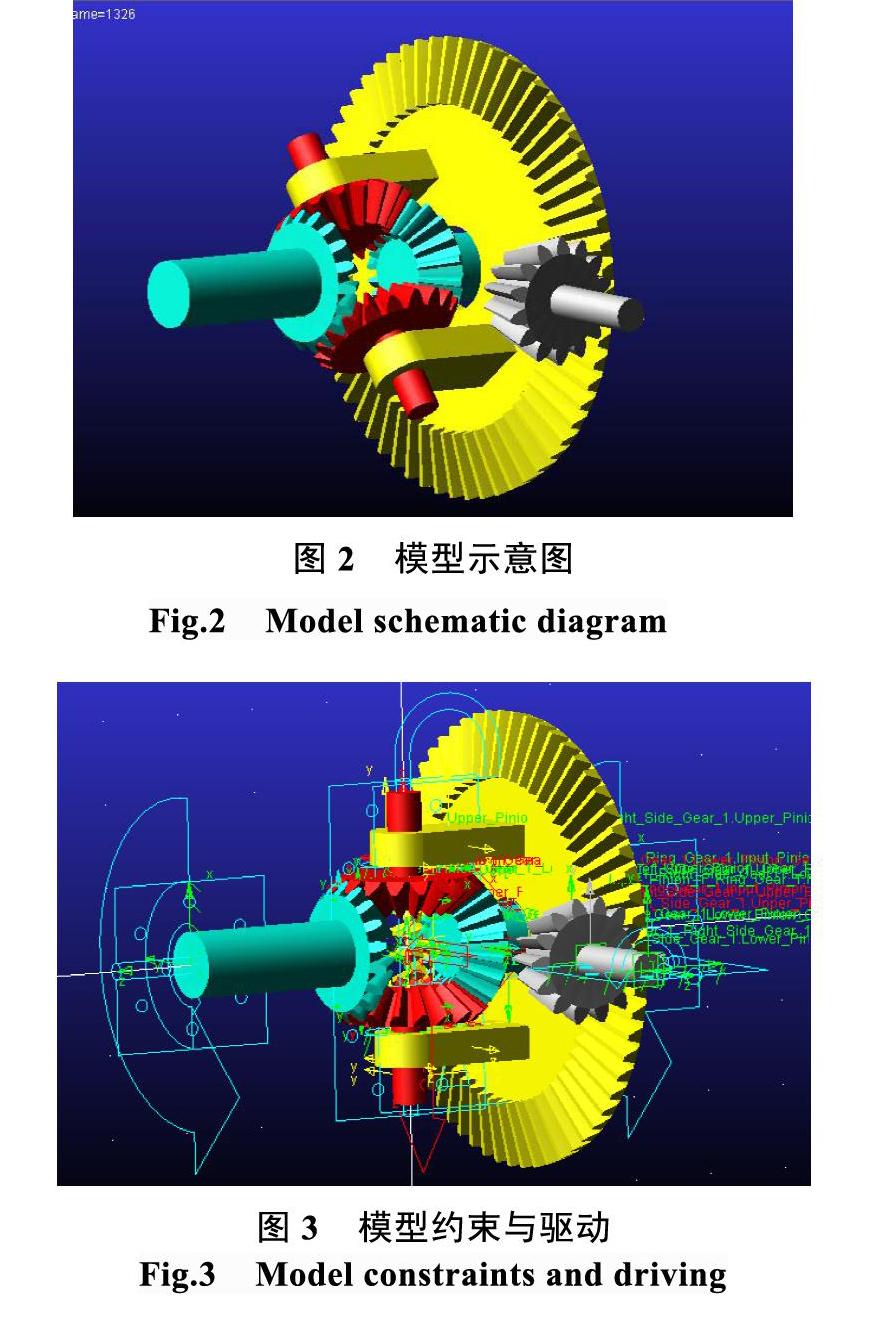
在打开adams/view界面后,设置合适的adams/view工作环境后开始创建设计点,该模型中共需要创建8个设计点,计算得出每个点的坐标后依次将每个设计点建立在大地上。基于建立的设计点,开始建立第一对齿轮,其中齿轮的齿数为18、齿宽为25.4、锥齿轮的节面角为45度、中心螺旋角的角度设为0,另一对齿轮与第一对齿轮基本参数相同,只有四个齿轮的中心点坐标不同。这两对齿轮一对为半轴齿轮,一对为行星轮。两对齿轮建立完成,建立从动齿轮(环型齿轮),然后建立主动齿轮。所有的齿轮建立完成后,建立左右两个输出半轴、输入轴,得三维实体模型如图2所示。
3.2 施加约束与驱动
约束是对模型中零件的运动进行限制,载荷是在模型上施加力,驱动模型运动。根据差速器工作和运动的实际情况,对其施加约束和载荷。齿轮和大地之间添加旋转副,齿轮和左右半轴之间添加固定副,对输入轴添加驱动函数完成驱动的添加。将所有的约束和驱动添加完成三维实体模型如图3所示。
4 差速器模型仿真与运动分析
在模型上进行设置仿真时间为5 s,仿真步长为0.001。完成建模和设置后进行仿真,并对仿真结果进行分析。
4.1 左右侧半轴齿轮运动分析
图4为左半轴齿轮角速度曲线,图5为右半轴齿轮角速度曲线,图6为主动齿轮角速度曲线,图7为从动环形齿轮角速度曲线。
仿真的前一秒时间内模拟的是汽车进行直线行驶时的左右两个半轴输出齿轮的转速,由图4和图5我们可以看出在动力刚开始输入是时汽车进行直线行驶,两个半轴输出齿轮的角速度完全相同。而在一秒之后仿真模拟的则是汽车进行左转弯时的情况,从图上我们可以明显看出汽车在进行左转弯时差速器的左侧半轴齿轮角速度明显减小,右侧半轴齿轮的角速度明显变大,这种情况反映在车轮上表现为汽车在进行左转弯时,汽车的左轮运动的距离较短,汽车的右轮运动的距离较长,而且从主动轴输入的驱动力经过差速器的分配,右侧半轴得到的驱动力大于左侧半轴得到的驱动力[9]。
通过图6图7我们可以看出输入动力的主动齿轮的角速度波动较大,但是通过从动环形齿轮的减速,从动环形齿轮的波动则相对小了很多。在图4和图5中我们还可以看出在输入角速度基本稳定时,无论汽车做直行或是做转弯,左侧半轴齿轮和右侧半轴齿轮两个齿轮的平均角速度保持不变。
4.2 行星齿轮运动分析
在差速器差速功能实现的过程中,起关键作用的是两个行星齿轮,具有动轴特性的行星齿轮将从动环形齿轮传递过来的动力分配到两个半轴齿轮上,并且分配的大小根据实际情况而自动调节。当左侧遇到较大的阻力时行星轮将较多的驱动力分配到右侧半轴齿轮上,当右侧遇到较大的阻力时行星轮将较多的驱动力分配到左侧半轴齿轮上。模型中上下两个行星齿轮的角速度如图8和图9所示。
由图可以看出两个行星齿轮的角速度曲线大致相同,将两条曲线作对比并放大如图10所示。
在上下行星齿轮角速度曲线放大图中可以清晰的看出上行星齿轮和下行星齿轮的角速度曲线基本重合,所以可以得出两个行星齿轮的角速度基本相同。在理论上两个行星齿轮与左右两个半轴齿轮完全啮合,所以两个行星齿轮应该有完全相同的角速度。但是在仿真中两个齿轮的角速度并不完全相同,这主要是因为齿轮在运行过程中存在较大的震动,因此两个齿轮的角速度并不完全相同。
5 结论
本文由ADAMS 软件建立了差速器的虚拟样机并对此进行仿真分析,将仿真结果与理论结果进行分析和对比,证明通过建立差速器模型并对其内部结构运动做仿真分析是可行的。差速器内两个行星齿轮的角速度基本相同,左右半轴齿轮的角速度之和恒等于差速器角速度的两倍。由仿真结果比较出各啮合齿轮的转动的异同点,更深入的了解差速器的工作原理。
参考文献
[1] 薛亮. 基于CATIA 和ADAMS的轎车差速器参数化设计及仿真[D]. 武汉理工大学硕士学位论文, 2011.
[2] 张晋西, 谭宇文, 谭芬, 等. 一种新型差速器设计及运动仿真[J]. 机械传动, 2014.
[3] 吴明. 自适应机械锁式防滑差速器的仿真与研究[D]. 湖南大学硕士论文, 2014.
[4] 陈双, 贺连梁. 汽车驱动桥新型差速器结构设计与运动分析[J]. 机械传动, 2016.
[5] 龙凯, 程颖. 齿轮啮合力仿真计算的参数选取研究[J]. 计算机仿真, 2002, 19(6): 87-91.
[6] 王裕清, 梁剑. 弧齿锥齿轮实体造型数学模型及其实现[J]. 中国机械工程, 2007, 18(14): 1660-1662.
[7] 方子帆, 舒刚, 何孔德, 等. 齿轮传动多体接触动力学模型[J]. 机械传动, 2009, 33(1): 15-18.
[8] 李润方, 王建军. 齿轮系统动力学[M]. 北京: 科学出版社, 1997: 11-14.
[9] 刘惟信. 汽车车桥设计[M]. 北京: 清华大学出版社, 2006: 214-230.
