一种带有最大能量跟踪的宽动态范围射频能量收集电路的设计
2019-10-09刘丹洋
刘丹洋,闫 娜,闵 昊
(复旦大学 专用集成电路与系统国家重点实验室,上海 201203)
射频(Radio Frequency, RF)能量收集是一种新的电力能量获取方式,通过天线收集空气中的离散RF信号或者特定RF能量源发射的RF信号,然后利用整流器将正弦波RF信号转换为稳定的直流电压,从而为后续电路提供稳定能量.这种自我从环境中获取RF能量供电的方式,可以突破传统电池供电所造成的对设备体积、寿命、维护成本等因素的限制,极大地扩大了无线传感器、射频识别标签以及嵌入式设备的功能,为以后的物联网发展打下了基础[1-2].
考虑到RF信号辐射对人体健康的影响,能量源发射功率根据协议受到限制,同时RF能量密度随着辐射距离的增大而大幅度衰减[1],因此工作在远距离的RF能量收集电路得到的能量密度非常小.针对这一点,以往的RF能量收集研究主要是针对核心电路整流器进行设计,通过改进整流器电路架构,来提高整流器的灵敏度以及能量转换效率(Power Conversion Efficiency, PCE),以此确保RF能量收集电路可以在尽可能小的能量密度下仍然可以工作,扩展了其极限工作距离[3-7].
在实际应用当中,由于RF能量源发射功率不同,接收感应射频能量的设备工作距离也不尽相同,导致输入到RF能量收集电路的功率变化范围特别大,因此需要RF能量收集不仅仅只在极限的工作距离能够达到很高的PCE,也需要在极限距离以内的任意地方同样能保持很高的PCE,这样才能提高能量收集电路灵活性,使得电路在不同的地方均能够从周围射频源中获取更多的能量.然而,由于整流器本身受到阈值电压和反向漏电的影响,还有整流器与天线失配的影响,RF能量收集电路往往只能在特定情况进行优化达到最高PCE,而在其他情况PCE迅速下降,这便导致能量收集电路高效率动态范围非常小,无法满足设计需求.由此,有研究人员的论文通过学习太阳能收集研究,加入辅助控制回路,进行最大能量跟踪,来解决该问题[8-10].
本文同样沿用太阳能收集加入辅助控制环路提升适应性的研究思路针对上述不灵活问题提出了一种用于RF能量收集电路的最大能量跟踪方法,通过采样存储不同整流器级数的输出电流进行比对,选取在当前输入功率下的最优整流器级数进行最大能量点跟踪.测试结果表明: 所设计的RF能量收集电路可以在保持较高的灵敏度下,在较宽输入功率动态变化范围均能达到很高的PCE.
1 RF能量收集的介绍
1.1 RF能量收集思路的框架
图1展示了RF能量收集电路的基本框架以及能量传递路径.RF能量源通过天线发射RF能量,之后发射的RF能量以电磁波形式辐射一定的距离后,由RF能量收集电路的天线得以感应接收,接着电路通过匹配网络将收集到的能量尽可能地传入到后面的整流器电路中,最后通过整流器电路将周期性的电磁波信号转换成一个稳定的直流电压,为后面的负载电路提供电力能量.

图1 RF能量收集电路的能量传输路径Fig.1 The energy transmission path of the RF energy harvester
根据Friss能量传输公式,RF能量收集电路从天线中获取的输入功率Pin可以表示为:
(1)
其中:Psource是能量发射功率;Gs是能量发射源天线增益;Gr是RF能量收集电路的天线增益;λ是接收信号的波长;d是能量源与能量收集电路的距离.在实际应用中,能量发射功率Psource以及工作距离d均会发生不同的变化,所以输入到RF能量收集电路的功率Pin也不相同.
评估RF能量收集电路的性能主要需要考虑PCE.在RF能量收集的能量传输路径中,能量传递需要通过匹配网络和整流器两部分,才能将接收到的RF能量转换为稳定的直流电压为负载供电,由此RF能量收集电路的能量转换效率ηPCE可以表示为:
(2)
其中:Pload是负载输出功率;Pin是天线获取的输入功率;Prec是整流器获得的功率;ηmatching是匹配网络转换效率;ηrectifier是整流器能量转换效率.式(2)表明: RF能量收集的PCE主要跟匹配网络和整流器两部分有关,提升这两部分的效率均可以提高电路的整体PCE.
1.2 RF能量收集电路的效率分析
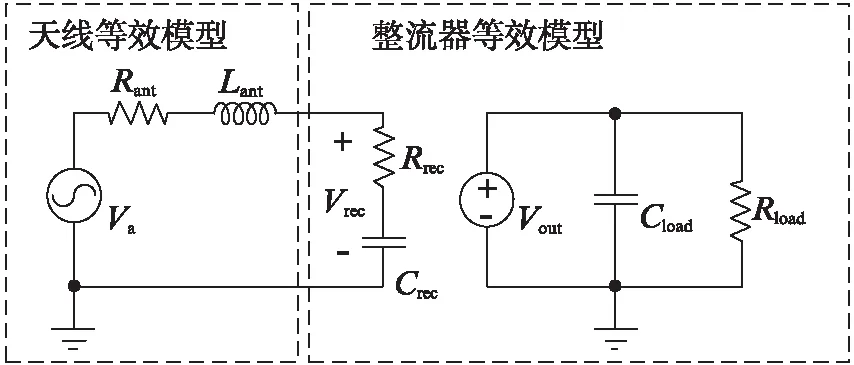
图2 RF能量收集等效模型电路图Fig.2 The equivalent circuit of the RF energy harvester
为了方便解释和分析RF能量收集电路的匹配网络效率,将RF能量收集电路简化为一个天线等效模型和整流器等效模型,如图2所示.其中:Va为天线上的感应电压;Vrec为整流器输入电压;Vout为输出电压;Rant和Lant分别为天线等效电阻和等效电感;Rrec和Crec分别为整流器等效电阻和等效电容;Rload和Cload分别为负载等效电阻和等效电容.
可以得到天线感应的电压Va与输入功率Pin关系:
(3)
传输至整流器的射频功率Prec可以表示为:
(4)
当天线阻抗和整流器阻抗满足共轭匹配时,整流器获得最大输入功率:
(5)
用Prec,max归一化Pin,得到匹配效率:
(6)
当设计好天线后,天线的等效电阻Rant和等效电感Lant得以确定,针对特定输入功率,仔细设计整流器的等效电阻Rrec和等效电容Crec,可以使天线阻抗与整流器阻抗共轭匹配,进而确保收集到的RF能量完全传递给整流器,来提高匹配效率ηmatching.但是实际整流器是一个非线性电路,在输入功率发生变化时,整流器的工作区域从亚阈值区域转变为饱和区,其等效阻抗也会发生一定的变化,导致与天线阻抗失配,进而减少了匹配效率ηmatching.
此外,整流器能量转换效率同样在不同输入功率下也会发生变化,在不同输入功率下需要择中阈值电压以及反向漏电影响.在低输入功率的情况下,输入到整流器的输入信号小于或接近于整流器阈值电压,导致需要采用新的整流器结构来克服阈值电压对输出功率的不利影响,从而提高整流器的PCE.然而在整流器输入电压不断增大后,克服阈值电压影响的电路仍然在工作,这时反向漏电反而会增大,导致该部分减少的效率抵消了克服阈值电压对效率的提升,从而降低了整流器能量转换效率ηrectifier.
由于以上两点因素,传统RF能量收集电路同时受到匹配效率和整流器效率两者的影响,无法获得较宽的高效率动态范围,不能使得电路在宽输入功率范围均能够保持高的能量转换效率.
2 级数调控整流器的研究与设计
2.1 级数调整方法原理介绍
在整流器设计当中,整流器可以采用级联的方式,实现倍压整流的功能,在输入信号较小的时候,可以将输入信号多倍放大输出,得到一个大的直流电压.
根据文献[11],多级级联整流器输出电压Vout可以表示为:
(7)
等效电导Grec和等效电容Crec分别表示为:
(8)
(9)
其中:Vout为输出电压;Pin为输入功率;Gant表示天线等效电导;GlossN和GlossFIX分别表示整流器跟随级数变化的等效电导和固定电导;Iload表示负载电流;n,VT,α,χ,Is均为二极管参数;Cc和Cpara分别为整流器耦合电容以及二极管寄生电容;f为输入信号频率.
根据上述分析可以看出,输出电压Vout、整流器等效电导Grec以及等效电容Crec均与整流器级数N有关.因此RF能量收集系统采用不同级数的整流器有如下好处: 1) 在输入功率Pin较小且负载电流Iload较小的情况下,根据式(7)可以知道,此时公式中的正值部分占主导地位,Vout与N成正比例关系,所以能量收集电路可以通过增加整流级数的方法来提高输出电压,从而提高电路的灵敏度;2) 在输入功率Pin较大的情况,由于输入功率的增大,供给负载的电流Iload也会增大,所以式(7)的负值部分带来的损耗开始显现,反而降低了级数提升带来的优势,所以可以减少整流器级数平衡两者的优势;3) 根据式(8)和式(9),当输入功率Pin增大时,整流器等效电导Grec也随之增大,而等效电容Crec中的Ccp也会随着晶体管工作区域从亚阈值区域进入到饱和区而增大,进而导致Crec增大,因此整流器的等效阻抗会随着输入功率的增大而发生变化.为了弥补该影响,同样可以采用减小整流器级数的方法进行遏制,让电路在宽输入功率变化范围内可以保持高的匹配效率.
结合以上三点考虑,在本文中,我们提出了一种级数调整的最大能量跟踪方法,如图3所示.在基本的RF能量收集电路框架上,加入了级数控制环路,自动检测3~5级整流器的输出电流,并进行比较,然后通过级数控制环路进行相应调整,以求达到最大能量跟踪,从而扩展RF能量收集电路的高效率动态范围.

图3 本文所提出的RF能量收集电路框图Fig.3 The block diagram of the proposed RF energy harvester
2.2 射频能量收集电路设计
本文所提出的RF能量收集电路具体细节如图4所示.该能量收集电路加入输出能量采样电路和级数控制环路,采样对比3~5级不同级数的整流器输出到电子负载的电流,在不同输入功率情况下,通过环路选择最佳级数,使得输出到电子负载的能量最大,从而进行不同输入功率下的高能量转换效率调控.

图4 带有级数控制环路的RF能量收集电路图Fig.4 The whole system circuit of RF energy harvester with stage control circuit
整体电路包括5部分: 可配置整流器、输出能量采样电路、级数控制环路、匹配网络、负载电路.可配置整流器、输出能量采样电路以及级数控制环路为芯片内部模块;匹配网络和负载电路为芯片外部模块.
可配置整流器为RF能量收集电路的核心模块,包括5个级联的整流器,并且分为两个部分.前2级整流器均为B类整流器架构,后3级为A类整流器架构.系统通过级数控制环路输出控制信号N1,N2,G1,G2来调整前2级整流器是否接入到工作链路中,由此实现3~5级整流器的配置.2种整流器电路架构如图5所示.

图5 可配置整流器组中的不同整流器架构Fig.5 The circuit of different rectifiers on the configurable rectifier
A类整流器为一种简化后的效率增强型动态整流器[12],相比于传统的动态整流器[6],该整流器加入了一个未带有负载的动态整流器作为辅助整流器,为主支路的动态整流器结构中MN1、MN2、MP1、MP2提供更高的过驱动电压,进而提高了整流器的灵敏度,并且扩宽了高效率范围.B类整流器是基于A整流器电路改进的受控型整流器,在射频信号的输入端RF+/RF-与耦合电容CC之间加入了NMOS晶体管MS1~MS6作为控制开关,在后面的环路中,状态机可以通过调整控制信号N来选择MS1~MS6的导通与否,进而调控是否使用该整流器级数.同时,在B类整流器的输出端,加一个NMOS晶体管MG作为控制开关,通过调整控制信号G来确保在不使用该级整流器时,将其输出端下拉到0 V,作为新整流器的输入地,减少受控型整流器不完全关闭而导致整体效率降低的影响.由于受控制的整流器级数为2级,所以控制信号包括N1,N2和G1,G2,具体控制方式如表1所示.

表1 3~5级数整流器控制信号

级数控制环路负责通过比较各个级数的输出功率采样信息进行比较,并在之后通过状态机(Finite State Machine, FSM)进行相应的级数调控.因为每次只有一种级数的整流器在工作,所以为了对比3种不同级数的整流器效率,控制环路采用分时采样的方法,用一个电容C1(C2)存储当前整流器输出功率信息,然后改变整流器级数,在下一个采样时间采用另外一个电容C2(C1)存储改变级数后的整流器输出功率,通过2个电容C1/C2获取了级数改变前和级数改变后的输出功率信息,然后进行对比来完成2个不同级数整流器的输出功率对比,从而获得能量转换效率的对比.基于该采样思路,级数调控电路的控制调整逻辑如图6所示.

图6 级数调控流程Fig.6 The flow for stage control
当复位信号CLR有效时,RF能量收集电路将进行初始状态设置,将整流器级数调整为5级,并且按调整顺序依次将整流器从5级调整到3级,之后通过电容C1/C2存储不同级数整流器采样电压(V5stage,V4stage,V3stage),再使用比较器COM比较采样电压得到调整信息,最后状态机根据调整信息输出进行相应的级数调整信号.如果V5stage大于V4stage,则将整流器级数重新调整回5级,确定5级整流器PCE最高,并且维持5级状态直到下一次复位,反之,则将整流器级数改变到3级,并且比较V4stage与V3stage,如果V4stage较大,则级数调整回4级并且维持直到下一次复位;否则,则保持3级状态.通过这样的级数调控,级数控制环路完成了不同级数输出能量的对比,并能够获取最佳级数,得到最大输出能量的跟踪.
3 电路实现与测试
3.1 射频能量芯片介绍

图7 芯片显微镜照Fig.7 The chip micrograph
所提出的RF能量收集电路在SMIC 55nm CMOS工艺下进行了流片,芯片照片如图7所示,其中核心电路面积为500μm×150μm,整体面积为975μm×800μm.在实际测试中,芯片通过FR4 PCB板上的π型匹配网络,将输入信号端与芯片射频端进行连接.仿真与测试得到连接线损耗与PCB寄生损耗一共为2dB.后面的测试结果是将去除连接损耗,计算进入到芯片的实际能量进行灵敏度和能量转换效率.
3.2 能量转换效率测试
为了对比不同级数整流器以及所提出整流器在不同输入功率下的PCE,并模拟大负载电容输出电压长时间稳定的情况,采用调节负载电阻的方法,保证输出电压Vout稳定在2V.RF能量收集电路的能量转换效率ηPCE可以表示为:
(9)
图8展示了工作在915MHz下,不同级数整流器以及本文所提出的整流器在不同输入功率下的能量转换效率的测试结果.从图8可以看出,该RF能量收集电路通过跟踪不同级数整流器的输出功率,选取最佳级数,结合不同级数的优势,在不同输入功率下均获得较高的能量转换效率.相比于5级整流器,最优级数整流器将最高能量转换效率从46.5%@-10dBm提高到了61.4%@-5dBm.与此同时,为了与其他文章的性能进行对比,在本文中,我们定义能量转换效率衰减到最高能量转换效率50%的输入功率范围定义为高能效动态范围.从图9中可以看出,该RF能量收集系统的高能效功率范围为30%以上能量转换效率的输入功率范围,即从-14dBm到5dBm,一共扩展到了19dB.

图8 在不同输入功率下的PCEFig.8 The PCE at different input power
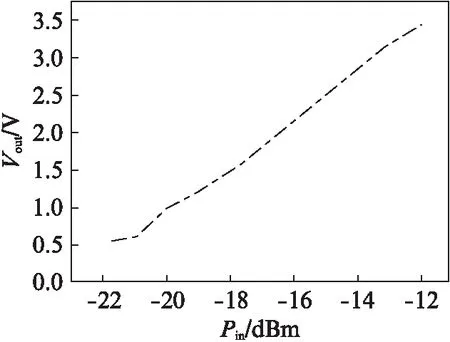
图9 所提整流器在电容负载下的输出电压Fig.9 The output voltage of the proposed rectifier with a capacitor loading
3.3 灵敏度测试
为了方便对比现有工艺的其他整流器性能,我们对灵敏度也同时进行了测试.可以从图9看出,在915MHz输入频率测试条件下,当负载为电容时,所设计的电路在输入功率为-20dBm时,可以获得1V的输出电压;在输入功率为-16.3dBm时,可以获得2V的输出电压.
3.4 性能对比
表2总结了本文所设计的RF能量收集电路的性能,并将其与近年来的国际先进水平进行了对比.由表2可见,本文设计的RF能量收集系统具有最大的最高能量转换效率和最宽的高效率动态范围.

表2 RF能量收集电路的性能总结
注:*表示能量转换效率高于最高能量转换效率50%的输入功率范围;**表示从所在文献测试图中获得.
4 结 语
针对传统RF能量收集电路无法在较宽的输入功率变化范围内均保持高效的问题,本文提出了一种最大能量跟踪方法,通过辅助电路控制整流器级数,在3级、4级和5级整流器中自动选取最优的级数,使得在不同输入功率下,RF能量收集电路均可以获得较高的能量转换效率,以此扩展RF能量收集电路的高效率动态范围.
测试结果表明,所设计的RF能量收集电路通过级数调整的方法,将最高能量转换效率从46.9%提高到61.4%,并且将高于最高能量转换效率50%的高效率动态范围扩展到19dB.与此同时,该电路仍然保持了较高的灵敏度,可以在驱动纯电容负载情况下,可以在-16.3dBm输入功率下,获得2V的输出电压.
