藏族历算五要素的计算器算法实现及相关概念剖释

拉毛吉

(西藏大学 中国藏学研究所，拉萨 850000))

依照传承时轮历可分为卓派(’bro lugs)和热派(rwa lugs)；依照理论可分为体系派(grub rtsis)和作用派(bye rtsis).体系派以《时轮根本续》为依据，因其理论体系完整而著称.学术界普遍认为《时轮根本续》在印度出现于公元624年左右.体系派又逐渐发展成粗朴派、萨迦派、布顿派、浦巴派、松巴派、国师派等小派别，并且各派有自己的代表典籍.(1)浦巴·伦珠嘉措于第八饶迥火兔年(公元1447年)撰写的《白莲亲教》(pad dkar zhal lung)；土观·却吉尼玛于第十三饶迥火龙年(公元1796年)撰写的《历算论·智者珍要》(mkhas pa’i snying nor)；松巴·益西班觉于第十三饶迥火兔年(公元1747年)撰写的《历算论普明心镜·格登新历》(dga’ ldan ’byor rtsis)；固始·洛桑弥觉多吉第十三饶迥火猪年(1767年)撰写的《历算论·极亮明灯母子篇》(rtsis zhung yang gsal sgron me ma bu)等为代表.这些小派别在原理、算法和基本数据上都大同小异，但各自的“算余”(rtsis ’phro)不同.作用派以《时轮摄略经》为依据，认为兼容了“外道”的数据，注重实际运用的方便.学界一致认为《时轮摄略经》在公元608年左右出现在印度.体系派和作用派的原理和算法相同，但基本数据不同，例如，二者恒星年和朔望月的值不同.体系派主张太阳6714405日运行18382周，[1]即一年约等于365.2706451963877太阳日，等于371又1/13=371.0769230769229个太阴日(计算器16位，计算依据为11312太阴日=11135太阳日).作用派恒星年数值为365日15刻31分1息121/707.二者的历元都是同一年同一天，即饶迥年角宿月上玄月初一日天明时，[2]但二者合朔不在同一时刻，体系派合朔时间为37漏刻43漏分2又140/707息，作用派合朔时间21漏刻20漏分，历元时刻不同导致二者的“算余”也不同.如果以现代天文数据为标准进行比较，体系派朔望月的数值非常精密，作用派的恒星年数值比体系派更优.然而，与其他派别相比较，体系派在藏区更受推崇，其中浦派的应用相对广泛.

无论哪一派，历算中最基础又重要的运算属五项基本要素数值的计算，通常称“五支”(yan lag lnga)或“五要素”(lnga bsdus)，具体指曜(gza’)、日期(tshes)、星宿(skar)、“会合”(sbyor ba)与“作用”(byed pa).曜为“定曜”(gza’ dag)，指真太阴日时刻，也是所求日准确的曜序数和该日内太阴日结束的时刻；日期为所求日的太阴日日期，与喜(dg’a)、善(bzang)、胜(rgyal)、空(stong)、满(rdzogs)五种名称配合使用；星宿为“伴曜月宿”(res ’grogs zla skar)，即太阳日开始时月亮的黄经；“会合”不是天文学意义上的会合周期，而是占星术上使用的重要参考数据之一，从0到26共有27种，对应不同的名称；“作用”是太阴日的前分和后分，从上玄月初一后分开始到二十九日前分之间称作“轮值作用”(’khor lo ’pho byed bdun)，二十九日后分与初一前分有固定的名称，故称“固定作用”(rtagpa’ibyed pa).本文以《藏历运算大全》(skar rtsis kun ’dus nor bu)“白莲亲教”(pad dkar zhal lung)理论为依据，进行计算器算法的说明以及相关概念与运算的解析与阐释.

1 积月

1.1 计算方法

积年乘以12，加上入年月数，乘以67，加上算余0，然后除以65，商为积月.在藏历中算余(rtsis ’phro)是指计算中积累的剩余数据，相当于余数，此处是指计算积月时，用65做除法运算后所得余数，故藏文称作“达如拉玛”(mda ’ru lhag ma)，“达”是数字5的异名，“如”是数字6的异名，专指由除数65除后的余数.

1.2 概念阐释与解析

1.2.1 积月或称“真积月”，藏文“tshes zla dag pa”，即太阴日积月，简称“zla dag”.意思是从近距历元到所求月份积累的总月数，包含积累年份中产生的闰月数.若求积月须知积年和入年月数.

需要强调的是此处积月为太阴日积月，涉及到时轮历三种日的概念.简单而言，依据太阳的运行、月亮的运行以及太阳在恒星背景的运行规律而得太阳日、太阴日和宫日三种概念.其中，太阴日是时轮历中最重要，也是最具特点的一个概念.藏历置闰方法、日月食的计算都与太阴日密切相关.

1.2.2 三种日的概念界定.时轮历规定太阳日是指从天明能辨认人手掌纹到次日天明能辨认掌纹的时间段；太阴日为月亮白分或黑分的十五分之一，即太阴月的三十分之一，具体数值推算见曜基数的分析与解释；宫年的定义是太阳在十二宫恒星周围运行一周的时间，恰好四季循环一周.此处，前半句表达的是恒星年的概念，而后半句为回归年概念.[2]165三种日的基本换算法：11312个太阴日等于11135个太阳日，149203个太阳日等于147056个宫日，65个宫日等于67个太阴日.

1.2.3 积年(入历年数，’das lo)，即以近距历元起到所求年份之间的年数.历元是指曾有一年，日、月、水星、金星、火星、木星、土星、罗睺、长尾九曜处于相同的方位，诸曜数据均归零，那一年是终尽年(zad pa)，次年是胜生年(rab byung).[3]纪年以“胜圣年”为首，是依据《胜乐经首品释》(stod ’grel)(2)《胜乐经》有上下两品，此处指上品之解释的书，与时轮续观点相同，作者为菩提圣心·恰那多吉(byang chub sems dpal phyag nag rdo rje).与《吠陀书》(rig byed)而说的.《胜乐经首品释》所说的胜圣年与汉历的丁卯年相一致.[2]11时轮历中认为诸曜数据归零后，次年即饶迥年(rab byung)角宿月上玄月初一天明时，除劫火(dus me)(3)劫火，即罗睺尾.时轮历中认为罗睺是一个有数无身的暗天体，其实是一个假象的天体，罗睺头与罗睺尾对应现代天文学之黄白交点的概念.外，其他诸曜的“恒加数”(rtag long)都首先入了白羊宫.[3]11-13饶迥年一般认为历元是1027年，实际计算中都使用近距历元，通常每60年更换一次历元.《藏历运算大全》历元为公元1987年，即第十七饶迥年的第一年，算余为零,其中，纪年的基本算法是所求之年份减去近距历元年份.

1.2.4 入年月数(’das zla)，自角宿月(nag zla)起至所求月之间的月数.角宿月是指月圆时月亮在天空的恒星周围位于角宿的月份.时轮历以角宿月为岁首，故藏历在算入年月数时以角宿月为基准起算，然而，实际演算前一年有闰月，且闰月在后半年，即在霍尔月九月至次年二月之间，此闰月要计算在入年月数中[4，5].

1.2.5 “达如拉玛”与二十四节气、闰月的关系：“达如拉玛”与时轮历平气、节等与二十四节气的安排有密切的关系，与闰月的安排亦有规律可循.当“达如拉玛”为48或49时，下一月即为闰月；当平气(sgang)在30日，下一月一定是闰月.闰月的产生是因为太阴月与宫月需要调和，而二者周期不一致，且无公倍数，故需要安排一个闰月来调和.一般情况下，夏至一定发生在藏历5月，冬至在11月，节(dbugs)在1至15日之间，平气在16至30日之间，不过，有闰月时日期会前移.

2 曜基数与太阳基数

2.1 算法

2.1.1 曜基数(gza’dhru).真积月加算余11024，乘以运转数8657，除以周期39592，减商，乘以39592，经过四舍五入，得“曜基数根本”(gza’dhru’gyur gzhi)，然后，乘以曜的运转周期7，除以39592，商为曜值；减商，乘以60，得数之整数为漏刻值；减整数，乘以60，得数之整数为漏分值；减整数，乘以6，得数之整数为息位值；减整数，乘以67，得数之整数为分母67的分子值；减整数，乘以707，四舍五入，得数为分母707的分子值.

2.1.2 太阳基数(nyi dhru).大阳基数的算法与曜基数算法相同，只是基本数据和各位的周期有所不同.算余为0，运转数为65，周期为804，太阳基数从高位到低位的周期依次为27、60、60、6、67.

2.2 概念剖析与解释

2.2.1 时轮历时间单位.时轮历最小的单位是“息”(dbugs)，其定义是壮年男子一呼一吸所用时间.息以上的时间单位一般用滴漏系统，一昼夜为60漏刻(chu thsod)，一漏刻为60漏分(chu srang)，一漏分等于6息.息以下没有时间单位一般叫“恰细”(cha shas)，即子位之意.实际运算中，用分数表达，分母不固定，尽量选用能使分子为整数的数值，必要时也会使用繁分数表示.正如此处选用的分母分别是67和707.那么，一昼夜的时间长度为21600漏刻.[2]165-166.

2.2.2 时轮历弧长单位.如前所述，时轮历周天的单位也是chu tshod，为了与表示时间的单位漏刻相区别，翻译为弧刻.一周天的长度为1620弧刻，每个宫所占的弧长平均为135弧刻，每星宿所占弧长为60弧刻；60弧刻除以4得1弧步，等于15弧刻；一个宫等于9弧步，即2又1/4个星宿.[2]9-10.

2.2.3 曜基数.曜基数按平太阴日计算，所求月之前一月三十日太阴日结束时所值曜序数及曜下余分.依据时轮历的宇宙结构理论，认为天穹宛如一把巨大的伞盖，伞面凹凸不平，二十八星宿和十二宫如同镶嵌在伞面上的宝石，他们在伞面上的位置固定不动，但整把伞随着风轮的顺时针旋转(4)藏文中描述为“gyas skor”，右旋的意思，实际指自东向西的逆时针旋转.而转动，因此，二十八星宿和十二宫在视觉上随着风轮的转动而自东向西做逆时针运转.这种旋转称作“视运动”(snang ’gros)或“风行”(rlung ’gros)，此概念等同于现代天文学的“周日视运动”.

“风行”每日旋转一周，对应不同的曜序(星期序数).时轮历曜序为：日曜1、月曜2、火曜3、水曜4、木曜5、金曜6、土曜0.此处的曜基数也是求风行一个月的时间内，在积月最后一日处于怎样的曜序以及该日是太阴日结束的时刻.此外，时轮历给出的平太阴月数据为29曜31漏刻50漏分0息480/707，有时也表示为29曜31漏刻50漏分0息45/67，345/707，前者余分母为707，后者划分为两位，分母分别为67和707.该数据是由太阴日和太阳日的关系，一个太阴月为30太阴日，而11312个太阴日等于11135个太阳日，故一个太阴日等于30乘以11135除以11312得到前文所述的太阴日数据，即1太阴日≈29.53058698726太阳日.

2.2.4 太阳基数.太阳基数为所求月平朔时太阳距春分点的弧长，即太阳的平黄经.[7]

3 “整数”与“零数”

3.1 算法

“整数”(ril ba)与“零数”(cha).真积月加算余1224，乘以253，除以3528，减商，乘以28，得数之整数为“整数”；减整数，乘以126，四舍五入，得“零数”.

3.2 解析与阐释

3.2.1 平太阴日.如前文所述，我们知道一个平太阴月的时间长度除以30得59漏刻3分4息16/707，约等于0.98435289957太阳日.但这是一个平均值，我们称作平太阴日.

3.2.2 宫月(恒星月).月亮绕地球运动，因天体的摄动，或者说受到近点月的影响，出现非匀速运动，在近地点附近运动速度快，在远地点附近运动速度慢，但每个太阴日内月亮所行的弧长相等，等于圆周长的三十分之一，与太阳在每个太阴日内带动月亮所行的弧长之和.

1周天为1620弧刻，根据三种日的关系，1宫年(恒星年)等于6714405/18382太阳日，乘以11312/11135等于371又1/13太阴日.太阳在每个太阴日内带动月亮所行的弧长为1620除以371又1/13，得4弧刻21弧分5息43/67，所以月亮在每个太阴日所行的弧长是58弧刻21弧分5息43/67.

月亮在恒星周围运行一周所经历的时间，即1620弧刻除以月亮在每个太阴日所行弧长，得27又657/869太阴日，等于27又395343/1228766太阳日，约等于27.32174太阳日.

3.2.3 “整数”和“零数”.是指月亮在所求月平朔距远地点(巨蟹宫)的整数与日下余分.[4]146(5)此处曜基数与太阳基数均以平朔(平太阴日结束时刻)来计算，即假设月亮是匀速运动.时轮历没有近点月这个术语，但认为月亮不均匀运动导致太阴月比平太阴月小2又1/126平太阴日周期，故30减2又1/126等于27.99206太阴日，即27.55407太阴日.

4 定曜与定日

4.1 算法

4.1.1 中曜(gza’ bar).真积月乘以30，加算余330720，再加所求日期值，乘以运转数11135，除以79184，减商，小数又乘以79184，四舍五入，得中曜根本；中曜根本乘以7，除以79184，得中曜，按M+键存储之.(此处，商为中曜之曜位数值，剩余各位数值的算法与求曜基数类同).(6)在藏文历算著作中“整数”与“零数”的计算是放在中曜之前来计算的，但笔者认为“整数”与“零数”的计算已经考虑了月亮的非匀速运动，因此，就理论逻辑而言，如果将二者的计算放在中曜之后，会更加容易理解.

4.1.2 月步(zla rkang)与半定曜(gza’ phyed dag).“整数”加所求日期，除以14，以商为依据做加或减的标记，商若为1或3，叫做“非均衡”(mnyam pa)，标记为加号；商若为偶数0、2或4，叫做“均衡”( mi mnyam pa)，标记为减号，减商，再乘以14，四舍五入，得余数，余数为步序(bya ra/rkang ’dzin)，根据步序查找月步表(见表1)，得积步记心上；基步乘以“零数”，除以126；若为前步，加积步；若为后步，用积步减之，减后按计算器上的+/-键去负号，(7)是前步还是后步，依据基步所在位置，日步表同理.得月步，然后，除以60；若之前除以14的商为均衡，加先前存入的中曜数值(按M+，再按MR)；若为不均衡，用中曜数值减之(按M-，再按MR)，得半定曜数值(8)此时，M+中存入的数据已更新为半定曜值..若求月步、半定曜各位数值，与求基曜各位算法相似.

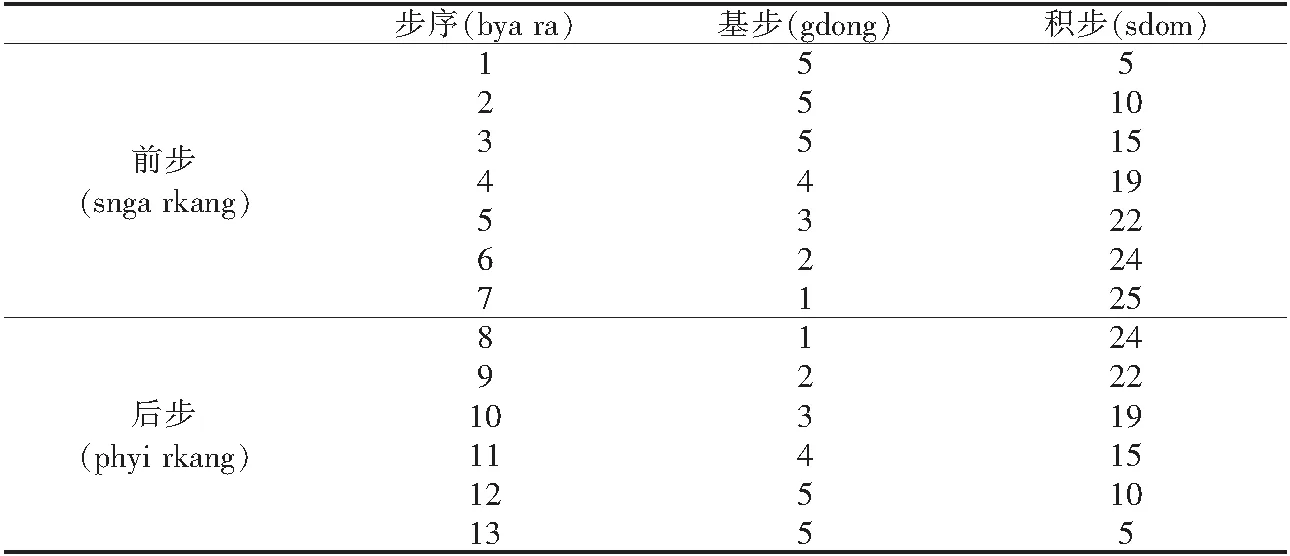
表1 月步表

4.1.3 中日(nyi bar).中日的算法与中曜类似，真积月乘以30，加算余0，再加所求日期，乘以运转周期13，除以周期4824，减商，小数乘以27得中日，按另一个M+键存储之.

4.1.4 定日(nyi dag)与定曜(gza’ dag).中日减6，若不够减，加27再减；余数若够减13，减之，够不够减记心上，得数乘以60，再减45，如果之前够减13，再减30，除以135，用商作日序查找日步表，积步记心上；减商乘以基步；若为前步，加积步；若为后步，减积步，按+/-键去负号，得日步，然后，除以60；如果之前够减半周期(13宿30漏刻)，分别加中日和半定曜，反之，分别减之，得定日与定曜.

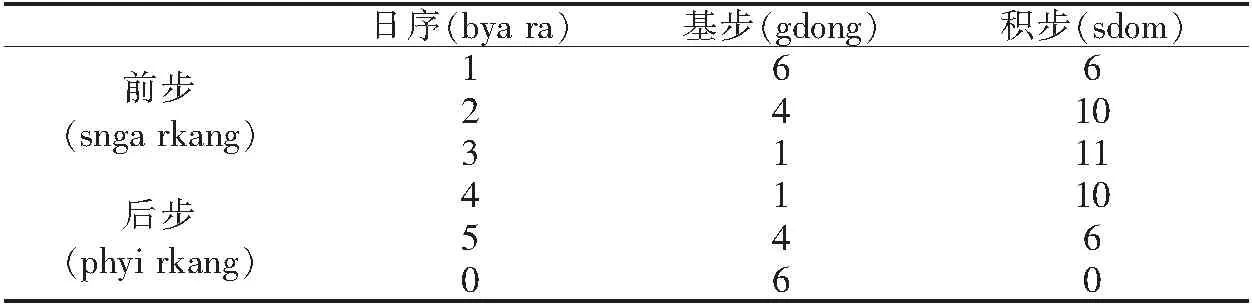
表2 日步表

4.2 概念阐释与运算解析

4.2.1 概念阐释

中曜：所求日平太阴日结束时的曜序及时刻，因尚未做月亮快慢运行的修正，所以只是求定曜的中间步骤值.

“基步”：藏文“rkang bzung gdong ma”，简称“gdong”，有时也叫乘数“sgyur byed”，对应汉历概念损益率.藏文名称是相对于积步而言，指进退变化的基本步数，两个连续的“基步”之和为次步的“积步”数值.此处指月亮从远地点(或近地点)开始每行一步，相对平均速度而言进行或退行的弧度.月亮非匀速地在恒星周围运行一周的时间即为近点月，近点月约为二十八日，所以作28步.因快慢运行的两个半周步数被认为是对称的，所以表格中只列出了14步的“基步”与“积步”.

积步：藏文为“rkang rdom”，对应汉历概念盈缩积，指从远地点起算到某曜所在的宿之间，各步退行(或进行)的损益率累积之和.月步：指考虑月亮的快慢运行后，月亮从远地点起算，真实行进的弧度.

中日：所求日平太阴日结束时，太阳距白羊宫首(或春分点)的弧长，也是该时刻太阳的平黄经.

定曜：藏文名称亦可对译为“真曜”，指真太阴日时刻，即所求日准确的曜序数和该日内太阴日结束的漏刻、漏分、息和子位数值.

定日：藏文名称可以直译为“真日”，即所求日太阴日真实结束时，太阳所在之宿和在该宿内已行过的弧度.

4.2.2 需要解释的运算步骤

第一，在半定曜的计算过程中，曜位不做具体加减运算，如果前述运算中用14所除的商为均衡(mnyam pa)，中曜值加月步值；若为不均衡(mi mnyam pa)，中曜值减月步值.通常来讲，中曜与月步单位不同，不能进行运算，但是由于二者周期几乎相等，近似为7，就直接进行了加减运算.[6]153第二，由月步算半定曜过程中，有一步是“除以60”，这是因为月步的最高位单位是弧刻，与中曜做加减运算时，需要进行单位换算.在求日步过程中也有一步骤是“得数乘以60”，这是因为45的单位是弧刻，所以得数首先要换算成弧刻位数值，再进行减法运算.由日步算定日过程中，也有“除以60”的步骤，与求半定曜的原因相同，此处也是把单位换算成宿位，再进行加减运算.第三，求日步时，“用中日减6宿45弧刻”是因为中日是以春风点为起算点，而积步和日步以远地点为起算点，6宿45弧刻是周天27宿的四分之一，从中日中减去6宿45弧刻意味着减去了春分点至夏至点的弧长；“减13宿30弧刻”是因为太阳运行周期是27，半周期为13宿30弧刻，如果够减半周，说明已经运行到了自近地点向远地点的半周，故要再加中日才能得到定日；“除以135”是因为一宫占九步，一步为15弧刻，即一宫占135弧刻，除以135就将原数据转化为宫数.

5 太阴日月宿、伴曜月宿与会合、作用

5.1 计算方法与例子

1)太阴日月宿(tshe ’khyud zla skar)：按MRC显示定日数值，加所求日太阴超行弧度宿位数值，乘以60，加太阴超行弧度漏刻位数值，除以60，得太阴日月宿.

2)曜伴月宿(res ’grogs zla skar)：按下位M-(减定曜)，得曜伴月宿.

3)会合：按上位M-(减定日)，得会合数值.

4)作用：所求日乘以2，减1，除以7，减商，乘以7，得后半日的作用(phyi cha’i byed pa)，然后间接推知前半日的作用(lnga cha’i byed pa).

5.2 概念解析与阐释

1)太阴日月宿：指真太阴日结束时，月亮所在之宿，即此时月亮的黄经.视运动而言，月亮与太阳向同一方向运动，每天除了共同的行度外，月亮还比太阳超行54弧刻，故定日加月亮超行弧度即为太阴日月宿.

2)“曜伴月宿”：相当于汉历中的太阳日月宿.指太阳日开始时，月亮所在之宿与该宿中已过的弧长.因为曜是起讫是按太阳日计算的，所以“伴曜”是按太阳日计算的意思，即天明时月亮的黄经.[6]195因此，也可以翻译为太阳日月宿.

3)会合与作用没有天文学相对应的概念，主要用于占算吉凶日.

6 总结

藏族天文历算时轮历中一些特殊的概念让初学者感到困惑，甚至具有多年演练经验的历算师亦不易解释其中的道理.造成这种状况的原因是教材编写注重记诵与演算.基本概念与数据在最后章节虽有涉及，但部分概念并未给出明确的含义，而是需要通过大量的数据演算来自己体悟.因此，本文认为使用计算器计算五要素时，关键要清楚以下三个方面：

第一，理论概念方面，曜基数、中曜与定曜，以及太阳基数、中日与定日的概念相似，容易混淆，要掌握这些概念，关键要掌握各个概念之间的联系和区别.曜基数与中曜并未考虑月亮的运行快慢，仅以匀速运动进行了平均数值计算，其中，曜基数是所求日之前一月平朔(即三十日平太阴日结束)数值，而中曜指所求日之平太阴日结束时的数值.定曜是兼顾了月亮受近点月影响做非匀速运动的情况下，真太阴日结束的准确数值.太阳基数、中日与定日概念理解的概念与曜相似，不同之处是太阳的相关数据单位是弧度，周期是自宿位、弧刻、弧分、息、子位依次是27、60、60、67；曜的相关数据单位是时间，周期自曜、漏刻、漏分、息、子位依次是7、60、60、6、67、707.

第二，在计算器的选择与功能方面，首先，需要选择位数尽可能多的计算器(现在市场上能够获得的最长数位的计算器为16位)，且计算器必须具备两位存储键.其次，要掌握计算器各个按键的功能，比如M+是存储键，同时也是将存储数据进行加法运算的键，M-是将存储数据进行减法运算的键，MR与MRC是显示存储数据或显示存储数据进行运算后的数据，MC是取消存储数据之键，AC是清零键，C是归零键等.

第三，实际计算方面，时轮历在沙盘上的演算以纯代数形式进行，所有数据均以整数或分数表达，而在计算器上只能计算整数或小数，因此，如何在计算器上实现时轮历算法，本质上成了如何在计算器上实现分数与小数相互转换的问题.以体系派平太阴月数值29日31刻50分0息45/67 345/707为例，转换为小数的方法为：{ [(〈29×60+31〉×60+50)×6×67+45]×707+345}÷707÷67÷6÷60÷60≈29.53058698727013；由此小数换算成时轮历分数的方法同求曜基数各位数值的方法，不再赘述.同时，也熟练掌握多位值与“个位”值之间的相互转换.以平太阴数值为例，由六位值转换为五位值，需要做类似现代数学中通分的计算：曜位、刻位、分位、息位数值不变，(45×707+345)÷67=480，480为五位值子位707的数值，即平太阴月也可以表示为29日31刻50分0息480/707.