连续区间Pythagorean模糊相似测度及其多属性决策方法*
2019-10-09林志超周礼刚薛明香
吴 越, 林志超, 周礼刚, 徐 鑫, 薛明香
(安徽大学 数学科学学院,合肥 230601)
0 引 言
多属性群决策[1]是现代决策理论的一个重要分支,在经济分析、工程管理、项目评估等诸多方面有着广泛的应用前景,而实际生活的很多情境中,决策者在决策过程中给出的评价经常具有不确定性.因此,Yager[2]提出了Pythagorean模糊集以考虑人类偏好固有的模糊性以及事物的不确定性.在处理多属性决策问题时区间Pythagorean模糊集[3]相较于Pythagorean模糊集更具有一般性,并能有效处理不完备信息.但是,一方面,区间Pythagorean模糊数因参数较多,在计算时复杂性较大;另一方面,在实际决策中,决策者积极、中立或是消极的风险态度对决策结果有非常显著的影响.因此,基于连续区间有序加权平均(COWA)算子[4],定义一种新的连续区间Pythagorean模糊平均(C-IVIFOWA)算子,将区间型Pythagorean模糊数转化为含参变量的Pythagorean模糊数.
相似性测度作为一个重要的信息度量工具,旨在描述和刻画两个集合的接近度,在模糊模式识别[5]、数据分类、多属性决策[6]等问题中起着决定性作用.文献[7]提出了模糊软集的相似测度;文献[8]基于直觉模糊接近度提出了一种直觉模糊相似测度;文献[9]定义了一种新的L型模糊相似测度.但现有文献对区间型Pythagorean模糊相似测度研究较少,本文将定义一种连续区间Pythagorean模糊相似测度,同时将其应用到多属性群决策中构建优化模型求解决策者权重和属性权重.最后,通过一个实例说明了该基于连续区间Pythagorean模糊相似测度的多属性群决策方法的效果.
1 预备知识

为方便计算,称α=[μA,νA]为Pythagorean模糊数.所有Pythagorean模糊数集合记作PFN.
定义2[2]设α=[μA,νA]∈PFN,则称
k(α)=(μA)2-(νA)2
(1)
为α的得分函数.其中,k(α)∈[-1,1].
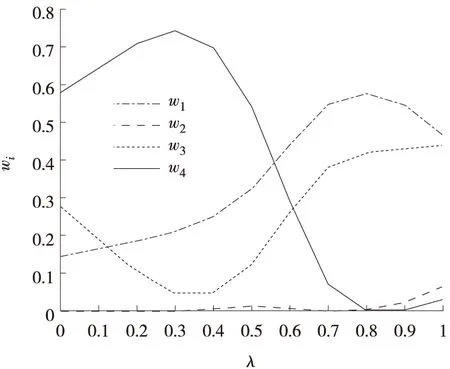
对任意两个Pythagorean模糊数α1、α2,若k(α1)>k(α2),则α1≻α2;若k(α1)=k(α2),则α1~α2;若k(α1) 定义4[4]设区间数[aL,aU],若函数f满足 (2) fQ([aL,aU])=λaU+(1-λ)aL (3) 由式(3)可以看出,COWA算子fQ([aL,aU])通过态度参数λ将区间数转化为含参数的实数形式,从而降低了其模糊性,并且COWA算子考虑了决策者风险态度对决策结果的影响,即态度参数λ的变化反映了决策者采取的不同风险态度.当λ=1时,fQ([aL,aU])=aU,表明决策者极度乐观;当λ=0时,fQ([aL,aU])=aL,表明决策者极度悲观;而λ=0.5时,fQ([aL,aU])=(aU+aL)/2,表明决策者态度中立.方便起见,fQ有时也表示为fλ. (4) (5) (6) 模型(a): (7) 模型(b): (8) 一种新的基于连续区间Pythagorean模糊相似测度的多属性群决策方法步骤如下: Step5 由式(8)计算方案的综合属性值ri(i=1,2,…,m),并根据ri对不同方案计算得分函数并进行排序,最后,选择最大得分函数值对应的方案为最优方案. 智能家居作为一个发展热点,是未来家居产业发展的一个必然趋势,作为新兴产业,具有极大的发展潜力.以一个智能家居工程为例,某智能家居企业有5个投资方案可以选择,构成了方案集X={x1,x2,x3,x4,x5}.企业聘请了3位智能家居领域的专家从经济性评价u1,可持续发展能力u2,原材料、能源及公共设施指标u3,不确定性与风险u44个方面对5个方案进行评价. Step2 取基本单位区间单调BUM函数Q(x)=x,即λ=0.5.通过C-IVPFOWA算子将区间Pythagorean模糊评价信息矩阵转化为Pythagorean模糊评价信息矩阵: Step4 根据模型,解得最优属性权重为ω*=(0.321 9,0.013 7,0.123 9,0.540 6). Step5 由式(9)计算方案的综合属性值,得 r1=(0.562 2,0.243 3),r2=(0.573 7,0.277 6),r3=(0.415 8,0.408 4),r4=(0.626 3,0.250 8),r5=(0.475 6,0.349 8).由此可得方案xi对应的得分函数值为k1=0.256 9,k2=0.252 1,k3=0.006 0,k4=0.329 4,k5=0.103 8.故排序结果为x4≻x1≻x2≻x5≻x3即方案4为最优方案. 以下考虑态度参数λ的变化对决策者最优权重与属性最优权重的影响.如图1所示,总体看来,最优决策者权重受到态度参数λ的影响大小不一.相较而言,态度参数λ对第2个决策者在决策时的权重影响较小,对第1个决策者及第3个决策者在决策时的权重影响较大.随着态度参数λ的增大,第1个决策者的权值不断增大,而第3个决策者的权重逐渐减小.由图2可知,属性最优权重仍受态度参数λ的影响.随着态度参数λ的变化,可持续发展能力u2评价指标的权重变化较小且接近于0,这反映了决策者在对方案进行评估时忽视了其可持续发展能力.经济性评价u1,原材料、能源及公共设施指标u3以及不确定性与风险u4评价指标的权重随着态度参数λ的变化,均存在明显波动.在态度参数λ较小,即决策者的评估态度比较谨慎时,不确定性与风险u4评价指标的权重较大,随着λ的逐渐增大,即决策者态度转为乐观时,该指标的权值显著降低.当态度参数λ较小时,经济性评价u1,原材料、能源及公共设施指标u3的权重较小,而当λ逐渐增大时,u1、u3评价指标的权重显著增加. 图1 λ对决策者最优权重的影响 图2 λ对属性最优权重的影响 λ对各方案xi得分函数的影响如图3所示.不难看出,态度参数的变化导致最优方案有所不同.随着态度参数λ的增大, 方案1、方案5的得分函数逐渐减小,方案2、方案4的得分函数逐渐增大,并且各方案的得分函数差异逐渐减小.当态度较为积极时,方案3、方案5较优.另外,方案3的得分函数较低,说明方案3始终为最差方案,故勿需考虑该方案. 图3 λ对方案得分函数的影响 基于区间型Pythagorean模糊环境提出带有决策者态度参数的连续区间Pythagorean相似测度及相应的多属性群决策方法.连续区间Pythagorean模糊有序加权平均算子(C-IVPFOWA)的主要优点是它可以利用态度参数处理区间Pythagorean模糊集结合时的区间偏差,从而降低参数的不确定性,并有效地降低了计算复杂度.基于C-IVPFOWA算子,提出了一种新的连续区间Pythagorean模糊相似性测度,并讨论其性质.利用该相似性测度,提出了基于连续区间Pythagorean模糊相似测度的决策者以及属性权重确定非线性优化模型,并讨论了态度参数对决策者权重、属性权重以及方案综合得分函数的影响,最后以实例分析说明了该模型的可行性和有效性.
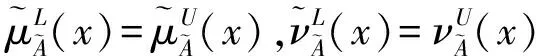
2 连续区间Pythagorean模糊相似性测度

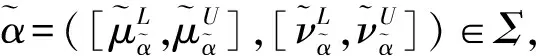
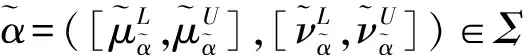
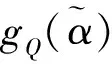



3 新的基于连续区间Pythagorean模糊相似测度的多属性群决策方法





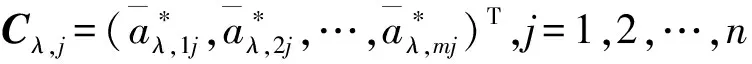



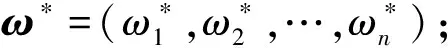
4 案例分析

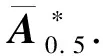


5 结束语
