不同惯性参考系中系统机械能是否守恒的再讨论——兼谈机械能守恒定律满足伽利略力学相对性原理

王志成 康旭红 王增发

(1. 甘肃省临夏市临夏中学，甘肃 临夏 731100; 2. 甘肃省积石山县民族中学，甘肃 积石山 731700)

1 一个争论已久的问题

近日阅读的多篇文章,[1-8]围绕一个中学物理中的典型例题,展开了机械能守恒定律与惯性参考系的选择有没有关系的大讨论,而且所持观点不同,结论也各异．文献[1-5]认为滑块的机械能在一个惯性参考系中守恒,另一个惯性系中可能不守恒,机械能守恒定律不满足伽利略力学相对性原理;文献[6-8]认为滑块的机械能在不同惯性系中都守恒,机械能守恒定律满足伽利略力学相对性原理．

笔者觉得,要讨论这个问题,首先要统一讨论的问题标准,即重力势能是属于系统还是属于滑块．只有讨论的问题的标准统一(否则有偷换概念之嫌),才有讨论的意义．

1.1 争论已久的问题

如图1所示,水平地面上固定一个高为h、倾角为θ的光滑斜面．有一质量为m的小滑块(可视为质点),从斜面顶端由静止沿斜面自由下滑,同时有一小车相对于地面以速度u向右匀速运动．试讨论地面参考系和小车参考系中,滑块机械能是否守恒．

图1

(有些文章的例题跟上述问题一样,也有些文章只是把地面固定斜面改为小车中的固定斜面．不影响问题的讨论)

1.2 典型分析

分析1：以地面为参考系,由于斜面支持力不做功,只有重力做功,机械能显然守恒．设滑块到达斜面低端时速度为v,有

(1)

所以

(2)

分析2：以小车为参考系,滑块初速度为-u,方向向左．设滑块到达低端时相对小车的速度大小为v′,由图2知

v′2=v2+u2-2vucosθ.

(3)

取地面为零势能面．滑块在斜面顶端的机械能为

(4)

滑块在斜面低端的机械能为

(5)

比较(1)、(4)、(5)式可知

Ek1+Ep1>Ek2+Ep2.

(6)

可见,以小车为参考系,滑块的机械能不守恒．

对这个结论,许多作者的解释是:在小车参考系中,斜面支持力与滑块的的速度v′不垂直,做了负功,所以滑块机械能减少了．(笔者注:后面分析中可以看出,滑块压力也对地球做了功,地球机械能有微小的增加,通常被忽略了)

对比分析1、分析2后,文献[1]产生了困惑:根据力学相对性原理,任何力学规律在任一惯性系内具有相同的形式．机械能守恒定律作为重要的力学规律,理应满足力学相对性原理．

2 定性论证不同惯性参考系中系统机械能守恒

首先,应统一讨论的问题标准,明确势能是系统共有的．普通高中课程实验教科书《物理》必修2第66页:必须指出的是,重力势能跟重力做功密切相关,而重力是地球与物体之间的相互作用．也就是说,倘若没有地球,就谈不上重力．所以,严格说来,重力势能是地球与物体所组成的物体“系统”所共有的,而不是地球上的物体单独具有的．

其次,明确运用机械能守恒定律的研究对象一定是系统,而不是单个的物体．普通高中课程实验教科书《物理》必修2教师教学用书第123页:要向学生指出,重力势能是由地球与物体所组成的系统所共有的,弹性势能是由因弹力的相互作用而组成的系统所共有的．因此,运用机械能守恒定律求解的对象是由相互作用的物体所组成的系统．

再次,明确参考系是指我们假设不动的物体．因为运动是绝对的,静止是相对的,所以选定某个物体为参考系,其含义是假定该物体不动．

2.1 地面惯性参考系中定性论证

以地面为参考系,滑块和地球(地球包括斜面,以后简称“滑块和地球为系统”)为系统．滑块沿斜面下滑的过程中,支持力和压力对滑块和地球不做功,只有重力做功,根据机械能守恒的条件[9]“在外力不做功和非保守内力不做功”可知,滑块和地球系统的机械能守恒．

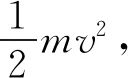
2.2 小车惯性参考系中定性论证

分析2中的根本错误是:分析机械能是否守恒时,只考虑了滑块的机械能,而遗漏了另一个重要对象——地球的初、末状态的动能．因此,得出了小车参考系中机械能不守恒的错误结论．

以滑块和地球为系统,在小车参考系中,地球不再是静止的．系统保守内力重力做正功．斜面对物体的支持力和物体对斜面的压力也是系统的一对内力,它们分别对滑块和地球做了功．众所周知,以地面为参考系时支持力和压力这一对内力的总功为0,根据“一对内力的总功与参考系无关”可知,在小车参考系中,虽支持力和压力分别对滑块和斜面做了功,但支持力和压力的总功仍为0,对系统不做功．

根据系统机械能守恒的条件“在外力不做功和非保守内力不做功”的条件下,小车参考系中,滑块和地球(包括斜面)系统的机械能一定守恒．

根据以上两个惯性参考系的定性分析,笔者的结论是:不同惯性参考系中,滑块和地球系统的机械能都守恒,机械能守恒定律满足力学相对性原理．

3 定量论证不同惯性参考系中系统机械能守恒

假设法是科学探究中的重要思想方法,大量应用于数学、物理研究中,是一种创造性的思维活动(百度语)．

对于滑块和地球系统的机械能是否守恒,可以用假设法定量论证．论证的逻辑思路如下.

由于这两式是经过大量实验检验并确认的、也是众所周知的正确的物理规律和结论．因此,只要假设不同惯性参考系中滑块和地球系统的机械能守恒,并由假设推导出与这两式相同的结果,就说明假设是正确的．

3.1 质心惯性参考系中定量论证

以滑块和地球为研究系统时,滑块沿斜面下滑的过程中,由于滑块有动量的变化,且滑块和地球(斜面)相互作用是内力,根据动量守恒定律可知地球也有动量的变化．由于地球质量很大,地球只是有微小的速度变化(通常忽略不计),但是严格的说,此时地面参考系(假定地面不动)不是严格的惯性系．所以,分析(1)中的(1)式和(2)式是近似式．

根据质心运动定理,滑块和地球之间的支持力、压力、万有引力都是内力,内力不会产生系统质心加速度,所以系统质心不动．因此,地球和滑块系统的质心参考系是一个很好的惯性系．

在质心惯性参考系中,由于滑块下落的时间(与地球自转周期24h相比较)内可忽略地球的自转．滑块在斜面顶端时,滑块和地球相对质心的速度均为0．设滑块从斜面顶端下滑到斜面低端时,相对质心的速度大小为v,此时地球相对质心的速度大小为V．并设地球质量为M、半径为R．

假设法：假设滑块和地球系统的机械能守恒,则有

(7)

根据动量守恒定律有

MV=mv.

(8)

由(7)、(8)式得

(9)

(10)

(11)

对质心惯性参考系中的结果,我们还可以做进一步讨论后,推广到地面惯性参考系.

(12)

由于M≫m,忽略二阶小量m2,所以(11)式中的

(13)

由(11)-(13)式得

(14)

考虑到M≫m和R≫h,由(9)、(10)式易得

(15)

V≈0.

(16)

上述3个近似式是精度极高的近似式,可以写成等式．(14)式、(15)式分别与地面参考系得出的(1)式、(2)式相同,说明假设正确．

即运用假设法证明了质心惯性参考系中,滑块和地球系统的机械能也守恒．

(16)式说明滑块下滑过程中,地球速度近似为0(精度极高的近似)．这就是我们通常可以把地面参考系看做惯性系的理由．

通过上述进一步讨论和推广,不仅加深了对地面参考系不是严格的惯性系的理解,同时也认识到地面参考系中的结论是精确度极高的近似结论．即质心惯性系和地面惯性系是近似(精度极高的近似)等价的．

3.2 小车惯性参考系中定量论证

在小车惯性参考系中,滑块在斜面顶端为初状态,滑块在斜面低端为末状态．则易得滑块和地球系统初状态的总动能为

(17)

滑块和地球系统末状态的总动能,如何简洁的求得呢?

以小车惯性参考系为固定系,那么质心惯性参考系是相对于小车惯性参考的平动惯性系．因此,可以根据柯尼希定理[10-11]求得滑块和地球系统在小车惯性系中末状态的总动能.(笔者注:考虑地球在质心系的速度后,也可以根据类似于图2的速度矢量关系求得地球相对于小车的速度,进而求得系统总动能,在此不再赘述,读者自己证明.)

根据柯尼希定理,质点组各质点的动能为质点组全部质量集中在质心并随质心平动的动能及各质点相对质心运动的动能之和．所以,滑块在斜面低端时,滑块和地球系统的末总动能为

(18)

式中V、v分别是地球和滑块相对于系统质心的速度.

结合(8)式、(18)式得

(19)

所以,系统初状态总机械能为

(20)

系统末状态总机械能为

(21)

假设法:假设在小车惯性参考系中,滑块和地球系统的机械能守恒,即E1=E2．由(20)、(21)式得

(22)

结合(8)式、(22)式易得

(23)

(24)

(25)

(23)-(25)式与质心惯性参考系计算出的结果(9)-(11)式一致．用不同的参考系分析出相同的结果,其实印证了同一客观事实的结论与选择的惯性系无关．

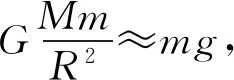
即运用假设法证明了小车惯性参考系中,滑块和地球系统的机械能也守恒．

4 结束语