高超声速滑翔飞行器再入轨迹快速、高精度优化
2019-10-09赵吉松张建宏
赵吉松,张建宏,李 爽
(1. 南京航空航天大学航天学院,南京 210016;2. 北京空天技术研究所,北京 100074)
0 引 言
高超声速滑翔飞行器在空天返回、远程快速打击等领域具有重要的应用背景。由于自身的气动布局以及恶劣飞行环境的影响,高超声速飞行器动力学模型具有高度非线性、强耦合及参数不确定等特点,因而其制导控制系统设计具有挑战性[1-5]。轨迹优化对于制导控制系统设计乃至总体设计具有重要意义。高超声速滑翔轨迹优化属于最优控制问题,其求解方法主要分为间接法和直接法[6]。间接法借助变分法或最大值原理,把泛函优化转化为两点边值问题求解;直接法通过对控制变量和/或状态变量进行离散把泛函优化转化为非线性规划(Nonlinear programming, NLP)求解。直接法中的配点法[6]由于不需要推导最优性必要条件,并且对初值的敏感性较低,容易收敛,近年来得到广泛研究。
高超声速滑翔飞行器再入轨迹优化问题[6]是复杂的多约束、非线性最优控制问题,优化计算量通常比较大。目前,以序列二次规划(Sequential quadratic programming,SQP)算法为代表的NLP求解器需要提供NLP的目标函数和约束对自变量的一阶偏导数甚至二阶偏导数。其中,基于一阶偏导数的NLP求解器只需要提供一阶偏导数,然后采用拟牛顿法构造近似的二阶偏导数,比如SNOPT[7];基于二阶偏导数的NLP求解器除了需要提供一阶偏导数,还需要提供二阶偏导数,比如IPOPT[8]。文献[9-12]研究发现,与直接计算NLP的偏导数相比,利用NLP的偏导数的稀疏性并且将其转化为轨迹优化问题对自变量的偏导数能够显著提高轨迹优化的效率。考虑到实际飞行器的气动数据通常为离散形式,本文研究采用文献[11]给出的稀疏差分方法,通过计算轨迹优化问题的一阶偏导数高效计算NLP的一阶偏导数,从而提高轨迹优化的效率。
由于受到热流、过载和动压等多种约束,高超声速飞行器再入轨迹通常是不光滑的。对于非光滑轨迹,如果需要高精度求解轨迹优化问题,均匀加密不是一种较好的方案。因为这样处理会导致计算量显著增加,需要更多的计算资源,并且随着节点数目的增加,算法的收敛性通常变差[13]。这种情况下有必要引入网格细化技术对节点进行局部加密或者调整,在轨迹变化平缓区域采用稀疏网格,在轨迹变化剧烈区域采用稠密网格。目前,国内外研究者在网格细化方面已做了不少工作[13-28]。对于局部配点法,由于离散格式本身对于离散节点分布没有限制,因而局部配点法的离散节点可以根据需要任意布置。适用于局部配点法的网格细化方法主要有小波分析法[13-14]、离散误差分析法[15]、多分辨率技术[16-21]、密度函数法[22]等。全局配点法(又称伪谱法或者正交配点法)的离散节点是正交多项式的根,其节点分布特点是中间稀两端密。全局配点法的优势是对于光滑问题具有非常高的代数精度,但是其离散节点不可以随意布置。因此,全局配点法在网格细化方面没有局部配点法灵活。全局配点法的网格细化方法通常是通过添加结点(段与段之间的连接点称为结点)将轨迹分段优化,利用结点附近的离散节点较密的特点达到加密网格的效果,比如结点伪谱法[23]以及各种自适应伪谱法[25-28]。分段优化的主要问题是通常很难确定需要分多少段以及在哪分段。若通过优化迭代确定这些信息会导致分段过多、采用的离散节点较多从而增加计算量等弊端[23-28]。为了提高网格选取的灵活性,文献[29]提出了一种适应于任意网格的伪谱法,但是随着非高斯网格区域的增加,方法的精度显著降低。
在众多网格细化算法中,多分辨率技术[16-21]具有吸引力。多分辨率技术的思想是分析离散节点的插值误差,如果某个节点的插值误差较大,则在该节点附近细化网格,否则不进行细化。多分辨率技术原理简单、鲁棒性好,并且采用的离散节点较少。文献[16-17]给出的多分辨率方法基于二进网格,其初始网格节点数必须是2j+1(j为整数),应用受到限制。文献[19-20]定义了一种节点数不受限制的广义二分网格,但是给出的网格细化算法要求初始网格节点数目必须是最粗糙网格的二倍,使用仍然不够方便。最近,文献[21]提出了一种新的广义二分网格,克服了这一缺陷。将这种新型网格与多分辨率技术相结合可构造出相应的网格细化算法。
本文研究采用稀疏差分法和基于新型广义二分网格的网格细化算法快速、高精度求解高超声速滑翔飞行器再入轨迹优化问题,并且通过优化落点区边界轨迹研究了再入飞行器的落点区范围。
1 再入轨迹运动模型
将飞行器简化为质点,记状态向量x=[r,θ,φ,v,ψ,γ]T分别表示飞行器的矢径、经度、纬度、速度、航向角和航迹角,那么描述飞行器质心运动的微分方程组为(忽略地球自转的影响)[6]
(1)
式中:g为飞行器受到的地球引力加速度,g=μ/r2;μ为地球引力常数。
空气动力产生的加速度沿飞行轨迹的切向、法向和侧向分量as,an,aw分别为
(2)
式中:σ为速度倾侧角;m为飞行器的质量。
升力和阻力的表达式分别为
(3)
式中:ρ为大气密度,采用美国标准大气模型(1976年)[30]插值计算;A为参考面积;CL和CD分别为升、阻力系数,Ma和α分别为马赫数和攻角。
图1给出升力系数和阻力系数随马赫数和攻角的变化特性[31]。与解析形式的气动数据相比,离散形式的气动数据更为常见,更具有代表性。

图1 气动力系数随马赫数和攻角变化规律Fig.1 Variation of aerodynamic coefficients with Mach number and angle of attack
2 再入轨迹优化问题
2.1 初始条件
高超声速滑翔飞行器的再入初始条件为
(4)
式中:h为飞行高度,h=r-Re,Re为地球半径。
2.2 路径约束
再入轨迹优化问题的控制变量为u=[α(t),σ(t)]T,其变化范围受到限制,即
(5)
式中:αmin和αmax分别为攻角的下边界和上边界;σmin和σmax分别为倾侧角的下边界和上边界。
为了使得高超声速滑翔飞行器安全返回,其再入飞行过程的气动加热受到限制,即
(qs)3D≤qU
(6)
式中:(qs)3D为三维驻点热流;qU为热流上限。
对于主曲率半径分别为R1和R2(R1≤R2) 的任意形状三维驻点,其热流表达式为[32]
(7)
式中:(qs)AXI为轴对称驻点热流,k=R1/R2。
轴对称驻点的热流表达式如下
(8)
式中:ρe和μe分别为边界层外缘(即正激波后)的气流密度和粘性系数,haw和hw分别为壁面恢复焓和壁面焓,壁面温度采用辐射平衡壁面温度。相关参数的计算方法参见文献[32]。
参数due/dx为驻点速度梯度,表达式如下
(9)
式中:u∞为来流速度大小;ρ∞为来流速度大小;ρs为正激波后气流等熵滞止密度(驻点密度)。
与其他轨迹优化研究经常采用的气动加热计算方法相比,式(8)和(9)给出的气动加热计算方法考虑了更多的影响因素,因而具有更高的精度,计算的驻点热流与风洞实验和高可信度CFD方法的结果比较一致[32]。此外,该方法能够考虑马赫数沿飞行轨迹的变化(以及由此导致的相关变量的变化),因而沿整个飞行轨迹都具有较高的预测精度。
2.3 末端约束
再入轨迹的末端约束参照航天飞机的末端能量管理窗口选取,具体取值如下
h(tf)=hf,v(tf)=vf,γ(tf)=γf
(10)
2.4 目标函数
横向航程是衡量高超声速飞行器再入机动能力的重要指标。本文取最大横向航程为优化指标。由于θ0=0°,φ0=0°,因而目标函数可写为
(11)
综上所述,高超声速滑翔飞行器再入轨迹优化问题描述为:确定控制变量u=[α(t),σ(t)]T,使得目标函数(11)最小化,并且满足状态方程(1),初始条件(4),路径约束(5)和(6)以及终端约束(10)。
3 快速、高精度轨迹优化技术
本文采用局部配点法[6]求解高超声速滑翔再入轨迹优化问题。局部配点法通过在一组离散节点上对轨迹优化问题离散化,将其转化为NLP问题。目前的NLP求解器(SNOPT、IPOPT等)在求解NLP时需要反复计算其偏导数。因此,提高NLP偏导数的计算效率对于提高轨迹优化效率具有重要意义。稀疏差分算法[9-11]通过分析NLP偏导数的稀疏特性,将NLP偏导数分解为原始轨迹优化问题的偏导数,从而能够显著减小计算量,并且不影响优化精度。此外,离散节点的数量直接决定了NLP的规模,与轨迹优化的计算量密切相关。多分辨率网格细化技术[16-17]能够采用较少的节点取得较高的优化精度。本文将稀疏差分法与多分辨率网格细化技术相结合,快速、高精度求解轨迹优化问题。
3.1 稀疏差分算法
采用基于梯度的算法(比如SQP算法)求解NLP时,需要提供其目标函数和约束对优化变量的一阶甚至二阶偏导数才能提高求解效率。为了高效计算偏导数,本文采用一种稀疏差分算法[11]。
以状态方程为例,将其写成如下向量形式
(12)
式中:x为n维状态向量;f为n维状态方程函数向量;u为m维控制向量;t为时间变量。
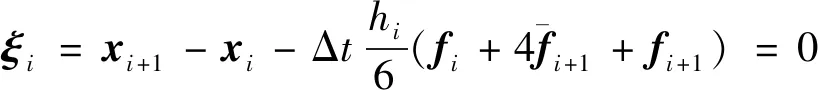
(13)
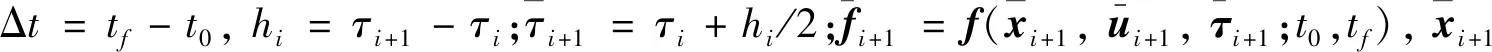
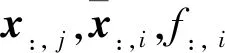
(14)
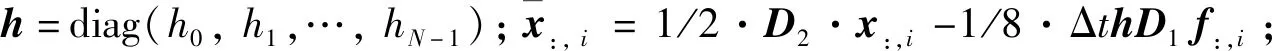
根据矩阵链式求导法则可得到状态方程离散格式约束对全部自变量的偏导数如下

(15)
可见,经过上述推导,状态方程离散残差约束(13)对自变量的一阶偏导数可以分解为原始轨迹优化问题的状态方程对其自变量的偏导数。将方程(15)与状态方程(1)相结合可以得到离散残差约束的偏导数矩阵的稀疏型(判断矩阵的每一项是否为零)和非零项的高效计算方法。采用类似的方法可以得到NLP的目标函数和其他约束对自变量偏导数的高效计算方法,具体参见文献[11]。由于原始轨迹优化问题的约束和变量的数量与离散后的NLP相比大幅度减少,因而这样处理可以显著提高偏导数的计算效率,从而提高轨迹优化问题的求解效率。
3.2 网格细化技术
传统的多分辨率技术基于二进制网格,其初始节点数目必须为2j+1,应用不方便。文献[19-20]定义了一种节点数不受限制的广义二分网格,但是要求轨迹优化的初始网格节点数必须是最粗糙网格的2倍,使用仍然不够方便。文献[21]定义了一种新型广义二分网格能够克服这一缺陷。本文将这种新型广义二分网格[21]与多分辨率技术[16]相结合构造网格细化技术,细化再入滑翔轨迹的离散节点。
在区间[0, 1]内,由N个均匀分布的初始子区间反复对分得到的广义二分网格为[21]
-1≤j≤Jmax
(16)
式中:整数j表示网格分辨率,整数k表示节点位置,整数Jmax表示网格最高分辨率。由于j的最小值为-1,因而整数N必须为偶数。采用Wj, N表示属于Vj+1, N但不属于Vj, N的节点,即
0≤k≤2jN-1}, 0≤j≤Jmax-1
(17)
因此,节点τj+1, k∈Vj+1, N满足如下关系
(18)
广义二分网格的子空间Vj, N满足嵌套关系,即V0, N⊂V1, N⊂…⊂VJmax, N,并且当Jmax→∞时,VJmax, N= [0, 1]。子空间Wj, N满足Wj, N∩Wl, N=∅(j≠l)。由定义和可知,二分网格是将区间[0, 1]不断对分获得,并且当k≥j时满足Wk, N∩Vj, N=∅。图2给出一组广义二分网格的示例(N= 6,Jmax= 5)。其中V0, N=V-1, N∪W-1, N通常作为初始网格。

图2 广义二分网格的示例(N=6, Jmax= 5)Fig.2 Generalized dyadic mesh with N=6 and Jmax= 5
对于一组离散最优解,多分辨率技术[16]的基本思想是在每个离散节点处通过其周围节点插值计算该节点的函数值。如果插值结果与离散最优解差别较大,则需要在该节点附近细化网格;否则不进行细化。为了应用多分辨率技术,需要结合轨迹优化的精度要求,选取初始网格参数N,对应于控制变量的细化误差限ε,最高分辨率Jmax和最大细化迭代次数Imax(Imax≥Jmax+1,Imax的默认值为Jmax+1)。赋初值I=1,Gold=V0, N,估计NLP的优化初值,将其记为Xold。那么,网格细化方法的流程如下:
1)以Gold为初始网格、Xold为初值求解NLP。若I≥Imax,结束算法;否则,转入下一步。
2)执行步骤(1)~(4),对Gold进行细化。
(1)令Φold={uj,k:τj,k∈Gold},并将其改写为Φold={φl(τj,k):l=1,…,m,τj,k∈Gold}。
(2)初始化中间网格Gint=V0, N以及相应的函数值Φint={φl(τ0,k)∈Φold, 0 ≤k≤N,l=1, …,m}。
(3)多分辨率细化算法。
(4)本次细化得到的非均匀网格为Gnew=Gint,对应的函数值为Φnew=Φint。
3)将变量I加1。如果细化后的网格Gnew与Gold相同,则停止细化;否则,将步骤1)求解出的NLP最优解插值到新网格Gnew,并以此作为新的优化初值Xold,令Gold=Gnew,返回步骤1)。
在上文网格细化方法的流程中,步骤2)对应的多分辨率细化算法是关键,具体算法如下:
1)赋初值j=-1。
2)求Wj, N和Gold的交集
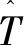
3)赋初值i=1,执行如下步骤(1)~(6)。
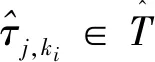


(5)将新增加节点对应的函数值添加到Φint。若新增节点对应的函数值未知,则利用网格Gold和函数Φold通过p阶ENO插值计算。
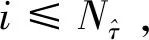
4)将变量j增加1。若j≤Jmax,则返回步骤2);否则,转入下一步。
5)结束本次迭代的网格细化算法。
4 仿真结果
本节应用稀疏差分法和多分辨率网格细化技术求解高超声速滑翔飞行器再入轨迹优化问题,以验证方法的有效性。轨迹优化的参数取值为:引力常数μ=3.98603195×1014m3/s2;飞行器质量m=17000 kg,气动力参考面积A=71.4 m2;控制量边界αmin=-10°,αmax= 35°,σmin=-90°,σmax= 90°;热流上限qU= 4.54×105W/m2;驻点主曲率半径R1=R2= 0.98 m;普朗特常数Pr=0.715;初始状态h0=79 248 m,θ0=0°,φ0=0°,v0=7334 m/s,ψ0=0°,γ0=0°;终端状态约束hf=24 384 m,vf= 762 m/s,γf=-5°。采用SNOPT 7[7]求解由轨迹优化问题离散得到的NLP。采用的计算平台为MacBook Air(处理器为Intel Core i5-5250U 1.6 GHz,操作系统为Windows 10企业版,编程语言为Matlab R2009a)。
4.1 最大横向航程轨迹
最大横向航程可用于评估高超声速滑翔飞行器的再入机动能力。采用本文第3节的方法研究该问题。网格细化参数取值为:N=20,ε=0.1°,Jmax= 3,p= 2,N1= 1,N2= 1。仿真结果表明,本文方法耗时约5 s即可优化出最大横向航程再入轨迹,单侧最大横向航程为25.85°(对应2874.5 km)。
图3给出优化的攻角和速度倾侧角随时间的变化曲线。图中圆圈为离散最优解,实线由ENO插值得出。网格细化算法共迭代4次,从321个均匀离散节点中选取74个节点描述最优攻角和速度倾侧角。由图3可知,最优攻角和速度倾侧角并非光滑变化,而本文方法能够在攻角和倾侧角变化较剧烈的区域加密网格,在其变化平缓的区域采用稀疏网格,整体效果是采用较少的离散节点高精度求解了最优攻角和速度倾侧角。如果采用相同数目的均匀离散节点,显然无法取得这种效果。
图4给出最优状态变量的变化曲线。图4中圆圈为离散最优解,细实线为采用数值积分方法(四阶Runge-Kutta方法)沿最优控制变量积分动力学微分方程得到的结果。可见,数值积分结果与离散最优解非常一致,证实了方法的精度。

图3 最优控制变量(74个节点)Fig.3 Optimal control solution(74 points)
图5给出驻点热流沿最优轨迹的变化曲线。从图5中的局部放大图可以看出,优化的驻点热流严格满足路径约束,再次展示了方法的精度。

图4 最优状态变量(74个节点)Fig.4 Optimal state solution(74 points)

图5 驻点热流变化曲线Fig.5 Time history of stagnation heating rate
为与前文了对比,图6给出采用开源最优控制程序GPOPS 4.1(其原理是hp自适应伪谱法[24])求解该问题得到的最优攻角和速度倾侧角。其中,GPOPS 4.1的网格细化迭代次数与本文方法相同,其余参数设置取GPOPS 4.1的默认值。仿真结果表明,GPOPS 4.1采用了228个离散节点描述最优解,将近是本文方法的3.1倍。分析图6可知,GPOPS 4.1除了在控制变量变化剧烈区域进行了细化,还在控制变量变化平缓区域进行了细化,而后者不是必须的,因此导致离散节点过多。可见,本文方法在精度相当的情况下,需要的离散节点数量较少。
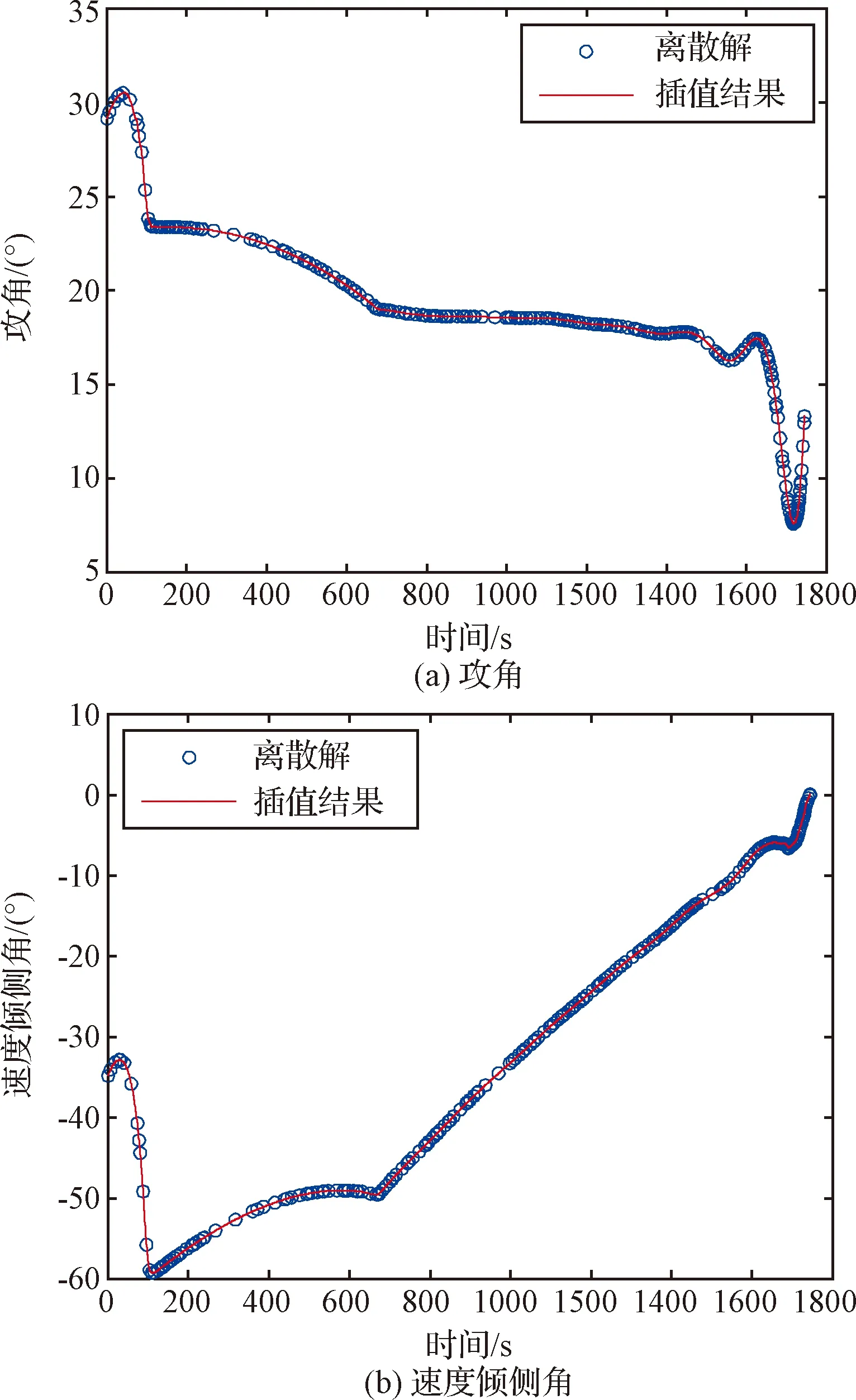
图6 hp自适应伪谱法求解的最优控制变量(228个节点)Fig.6 Optimal control solution from hp adaptive pseudospectral method (228 points)
4.2 再入落点区
高超声速滑翔飞行器的再入落点区对于飞行器返回机场的设计、应急机场的选取,以及高超声速再入滑翔武器的攻击区分析等具有重要意义。本文首先采用轨迹优化方法得到最大纵向航程轨迹和最小纵向航程轨迹,然后在不同的纵向航程约束情况下分别优化最大横向航程,得到了再入落点区的边界(轨迹优化的初始条件、路径约束和终端约束与最大横向航程问题相同)。图7给出右侧再入落点区的若干条边界轨迹(由于不考虑地球自转,左侧再入落点区与右侧再入落点区呈对称分布)。为了便于展示,图中还给出了再入轨迹在地球表面的投影以及落点区的边界。可见,高超声速滑翔再入飞行器能够在利用气动力在大范围内机动飞行。

图7 再入飞行器右半侧落点区边界轨迹示例Fig.7 Examples of trajectories at the boundary of reentry vehicle’s right-half landing footprint
将对应于不同纵向航程的落点区边界轨迹的末端位置相连即可得到落点区边界,如图8所示。图中的符号“+”表示飞行器的初始再入点位置,即(θ0,φ0)=(0°, 0°)。可见,再入飞行器的落点区接近于椭圆形,纵向范围θ=12.62°~102.81°(对应1401.1~11 432.3 km),横向范围φ=-25.85°~25.85°(对应-2874.5~2874.5 km)。高超声速滑翔飞行器能够在满足轨迹约束的情况下到达落点区内的任意位置。由于本文研究中没有考虑地球自转的影响,因而落点区呈左右对称分布。若考虑地球自转,那么落点区的形状会发生畸变,不再对称分布;但是这种变化相对于落点区范围而言通常比较小。
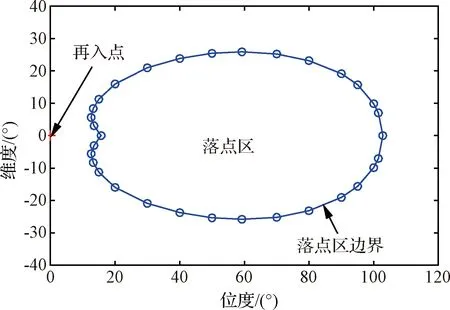
图8 再入飞行器落点区边界Fig.8 Boundary of entry vehicle’s landing footprint
5 结 论
本文研究了采用稀疏差分法和网格细化技术快速、高精度求解高超声速滑翔飞行器三维再入轨迹优化问题。建立了与实际工程问题比较一致的三维再入轨迹优化模型(含有热流约束、控制量边界约束和末端能量窗口约束等,采用离散大气模型、离散气动数据和较为详细的驻点热流模型)。从两个方面研究了提高轨迹优化的效率:1)采用了一种高效的稀疏差分法分析由轨迹优化问题离散得到的NLP一阶偏导数的稀疏特性并给出NLP偏导数非零项的计算方法,从而提高了NLP的求解效率;2)采用了一种新型基于广义二分网格的网格细化算法对离散节点进行细化,以较少的节点高精度描述最优控制变量,从而在保证精度的前提下进一步减小轨迹优化的计算量。仿真结果表明,所述方法在桌面计算机上耗时约5 s即可优化出一条严格满足各种约束的三维最优再入轨迹,并且数值积分结果与优化的离散解非常一致。此外,所述方法能够快速分析高超声速滑翔飞行器的再入落点区,进一步证实了方法的有效性和应用潜力。
