CE5T拓展试验轨道精度分析
2019-10-09欧阳琦段建锋
张 宇,孔 静,陈 明,欧阳琦,段建锋
(北京航天飞行控制中心,北京 100094)
0 引 言
2014年10月24日,探月工程三期再入返回飞行试验任务CE5T飞行试验器发射升空,11月1日05时服务舱和返回器分离,返回器在预定区域安全着陆,服务舱开始独立飞行,其飞行试验轨道如图1所示。为最大限度地利用服务舱的设计能力,尽可能为后续探月及深空探测开展技术试验验证工作,本文利用服务舱积累的实际在轨飞行数据,对CE5T拓展试验期间的轨道精度进行分析,能为后续任务提供轨道及其它技术支持。

图1 CE5T任务飞行轨道示意图Fig.1 Sketch map of CE5T mission orbit
CE5T服务舱拓展试验项目设计的飞行试验轨道包括5个阶段,经过大椭圆停泊轨道、地月转移轨道、地月L2点环绕轨道、近月制动,最后进入环月轨道飞行,开展交会对接远程导引试验、采样区成像、轨道环境探测及搭载设备试验等拓展试验项目。拓展试验完成后至今,服务舱依然在绕月正常飞行。
2014年11月1日,服务舱在近地点升轨完成后,进入绕地16天的大椭圆轨道,2014年11月17日,服务舱完成近地点变轨后,进入地月转移轨道。此后,服务舱于11月23日到达近月点,并在近月点完成变轨控制,进入飞往地月L2点的转移轨道。从11月1日升轨完成至11月23日近月控制这段时间的服务舱轨道是绕地大椭圆轨道,与以往探月任务的地月转移轨道类似[1-7],但不同的是2014年11月1日至2014年11月17日的飞行轨道远地点超过了白道范围,达到了50万km,飞行时间较长,轨道控制次数较少,这为轨道分析提供了便利,本文利用一整圈测量数据分析绕地大椭圆轨道的定轨策略和定轨精度。
2014年11月27日服务舱进入环绕地月第二平动点(L2)的李萨如轨道,开展了地月L2点环绕探测试验。李萨如轨道在旋转坐标系下X轴振幅约2万km,Y轴约4万km,Z轴约3.5万km,周期约14天。其中11月28日至12月26日服务舱环绕L2点飞行了两圈,作为我国首次绕地月L2点飞行的卫星,分析服务舱的轨道精度可以为后续地月L2点绕飞轨道提供支持。地月L2点是地月引力平衡点[8-11],本文分析了以地心为中心和以月心为中心两种不同参考系下轨道动力学差异和定轨精度。
服务舱从地月L2点转移到近月点附近后,通过三次控制使服务舱进入高度约200 km、倾角43°的环月轨道。以往探月任务环绕月球飞行的轨道倾角均为90°左右,而本次拓展试验是针对CE5月球轨道交会对接任务设计的飞行轨道,飞行轨道特性的不同对轨道动力学带来了一定的不确定性,从而影响轨道确定的精度[12-15]。近月轨道动力学影响最显著的部分是月球非球形摄动,月球非球形摄动的精度与重力场模型息息相关,本文主要利用重力恢复与内部实验室(Gravity recovery and interior laboratory,GRAIL)、月球勘探者LP165、月亮女神卫星重力场模型SGM100这三类具有代表性的模型分析对轨道精度的影响。
1 绕地大椭圆轨道的CE5T定轨
1.1 动力学模型
图2给出了拓展试验初期的轨道示意图,CE5T服务舱在2014年11月1日至2014年11月17日的飞行轨道是绕地大椭圆轨道,其中11月9日有一次轨道控制,结合该特征事件得到两个定轨弧段,第一时段是:2014年11月1日服务舱升轨控制后至11月9日远地点(53万千米)控制前,第二时段是:2014年11月9日远地点控制后至11月17日近地点(600 km)控制前。

图2 CE5T服务舱绕地飞行轨道示意图Fig.2 Sketch map of CE5T in Earth orbit
针对该轨道的特点,设置动力学模型和参数如表1所示。

表1 服务舱绕地飞行轨道动力学模型及参数Table 1 Dynamics model and parameters of CE5T satellite
结合表1中的轨道动力学模型及参数,利用11月1日服务舱升轨控制后的初始轨道,分析第一时段轨道动力学各摄动力影响,计算结果如图3所示。

图3 CE5T服务舱绕地飞行轨道动力学影响Fig.3 Dynamics influence of CE5T in Earth orbit
由图3可知,随着时间变化,服务舱与地球的距离增加,相应的地球质点引力加速度从10-2m/s2降低为10-3m/s2量级,随之月球质点、太阳质点以及其它大行星质点作为第三体引力摄动影响均有一定增加,月球质点、太阳质点引力摄动量级相当,太阳光压摄动影响为10-7m/s2量级。服务舱在此轨道飞行条件下的轨道确定成为弱引力约束的轨道动力学问题。弱引力特点是中心天体加速度相对环绕轨道时低数个量级,同时中心天体加速度相对摄动加速度差异不明显。
1.2 基于不同数据类型组合的定轨精度分析
根据动力学影响本文将第一时段和第二时段数据分别进行统计定轨[16],其中11月1日至11月9日的跟踪包括:统一S频段(Unified S-band,USB)跟踪测站青岛站(QD)、喀什18 m站(KS18)、喀什深空站(KSSK)和圣地亚哥站(STG),甚长基线干涉(Very long baseline interferometry,VLBI)测量站上海站(SH)、北京站(BJ)、昆明站(KM)和乌鲁木齐站(UL)。USB测量每天跟踪3~4 h,VLBI测量有3个跟踪弧段,依次为11月2日、11月5日和11月8日。11月9日至11月17日的跟踪包括:青岛站、喀什18 m站、喀什深空站,甚长基线干涉测量包括3个跟踪弧段,依次为11月10日、11月13日和11月16日。
统计定轨求解参数包括:历元点位置速度,光压系数和测站系统差。服务舱在巡航阶段采用对日定向模型,太阳帆板法向对准太阳,姿态保持固定,整个阶段的面质比不变,求解1个光压系数,USB测站的系统差按每天一组进行估计,如果求解全部测站的系统差会导致解算值异常,需设置一个跟踪时间较长且性能较好的测站不解系统差,本文以深空站测距为基准,为轨道指向提供约束。
由于当前定轨分析的两个定轨弧段均包含多天测量数据,为提高计算效率,需要分析不同的数据组合,使之既能保证计算精度,又能提高计算效率,具体计算策略如表2所示。

表2 服务舱拓展试验轨道确定数据使用策略Table 2 Strategy of tracking data in orbit determination
表2中第1~2类策略分别验证USB测量测距和测速的定轨贡献能力,第3~4类策略分别验证VLBI测量时延和时延率的定轨贡献能力。利用当前测轨弧段中所有高精度测量进行融合定轨的结果作为基准(即第5类策略),然后将前4类策略的计算结果与基准的星历进行比较,统计误差最大值如表3所示。
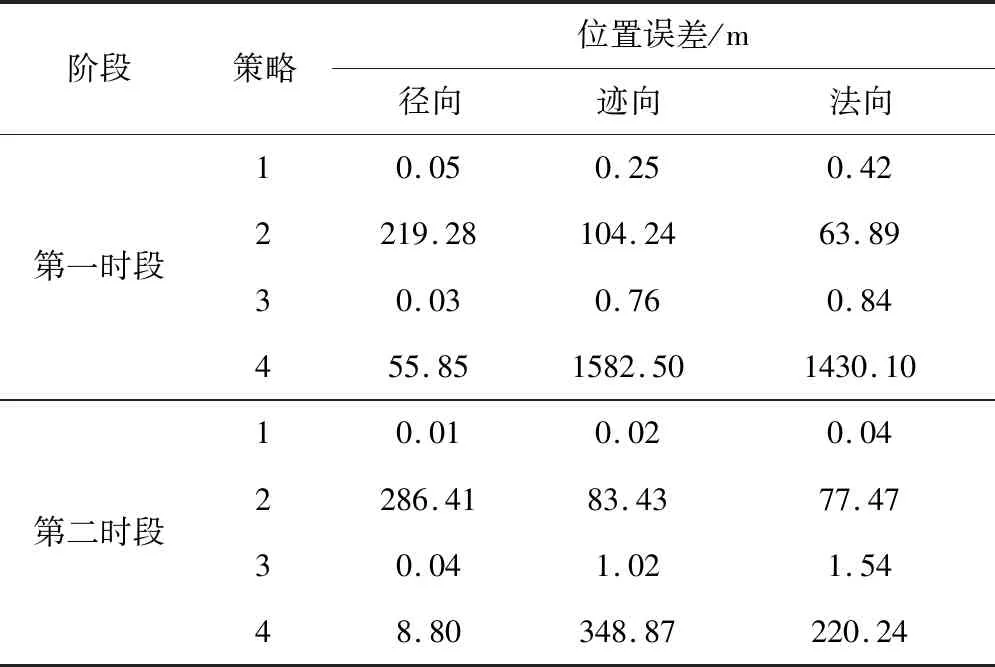
表3 服务舱使用不同数据类型定轨偏差Table 3 Position error of orbit determination with difference tracking strategy
根据表3两个时段的分析可知:测速的贡献精度小于1 m,测距的贡献精度为百米量级,其中径向误差最大,说明测距可约束轨道的径向,时延率的贡献精度约1 m左右,时延的贡献精度为千米量级,其中径向误差最大,说明时延可约束轨道的迹向和法向,测量数据对精密定轨的贡献从高至低依次为:VLBI时延、USB测距、VLBI时延率和USB测速。为提高计算效率,将精密定轨内符合误差截取到1 m,考虑到时延率数据量不大且测量精度较高,在测量弧段较少时对轨道精度会有一定改善,后续计算基准轨道的数据使用策略是:测距+时延+时延率的组合,第一时段定轨残差如图4所示。由图4可知,USB测距拟合残差小于5 m, VLBI时延拟合残差小于2 m,时延率拟合残差小于1 mm/s,将该结果作为基准轨道,可用于其它策略的比对分析。

图4 CE5T服务舱绕地飞行轨道定轨残差Fig.4 Orbit determination residual of CE5T in Earth orbit
通过计算重叠弧段星历偏差分析大椭圆轨道精度,其中第一时段首先计算11月1日至11月6日的轨道,然后计算11月4日至11月9日的轨道,重叠弧段为11月4日9时至11月6日17时,两组轨道定轨策略一致;第二时段首先计算11月9日至11月14日的轨道,然后计算11月12日至11月17日的轨道,重叠弧段为11月12日10时至11月14日12时。单USB定轨则采用测距+测速的策略计算的星历与基准进行比较,两组轨道重叠弧段星历偏差以及单USB定轨偏差如图5所示。
图5(a)表示第一时段重叠弧段星历偏差,起始时间为11月4日0时,图5(b)表示第一段USB定轨与精密定轨比较偏差,起始时间为11月1日0时;图5(c)表示第二时段重叠弧段星历偏差,起始时间为11月12日0时,图5(d)表示第二段USB定轨与精密定轨比较偏差,起始时间为11月9日0时。两组重叠弧段轨道星历误差均为百米量级,USB定轨的误差均为千米量级,其误差随服务舱与地球距离增大而增加。

图5 CE5T服务舱绕地飞行轨道星历误差Fig.5 Ephemeris position error of CE5T in Earth orbit
综上所述,服务舱在绕地大椭圆轨道的定轨是以地球为中心的弱引力动力学求解问题,通过分析两组时间段的定轨结果,得到了不同数据类型对定轨精度的贡献以及单USB定轨精度,其中精密定轨精度为百米量级。
2 地月L2点绕飞轨道的CE5T定轨
2.1 动力学模型
图6给出了环绕地月L2点轨道示意图,CE5T服务舱在2014年11月28日至2014年12月26日期间环绕地月L2点飞行,其中12月11日有一次轨道控制,结合该特征事件得到两个定轨弧段,第一时段是:2014年11月28日服务舱进入环绕地月L2点控制后至12月11日轨道维持控制前,第二时段是:2014年12月11日轨道维持控制后至12月26日控制前。由于环绕地月L2点轨道处于地月引力平衡点附近,轨道动力学积分中参考中心需要利用以地心惯性系和月心惯性系为代表的两种动力学模型进行分析,其中地心的动力学模型及参数设置参考表1,月心的动力学模型及参数设置如表4所示。

图6 CE5T服务舱环绕地月L2点飞行轨道示意图Fig.6 Sketch map of CE5T circle libration L2 point of Earth-Moon system
结合表1和表4中的轨道动力学模型及参数,利用服务舱进入环绕地月L2点后的轨道分析2014年11月28日至2014年12月11日的动力学影响,两种不同积分中心下计算结果如图7所示。
图7(a)表示以地心轨道计算的加速度,图7(b)表示以月心轨道计算的加速度。由图7(a)和7(b)对比可知,地心和月心积分的地月质点引力量级相当,在月心积分的太阳和其它大行星的第三体引力摄动量级更大。

表4 服务舱地月L2点绕飞轨道动力学模型及参数Table 4 Dynamics model and parameters of CE5T circle libration L2 point of Earth-Moon system

图7 CE5T服务舱地月L2点绕飞动力学影响Fig.7 Dynamics influence of CE5T circle libration L2 point of Earth-Moon system
2.2 基于不同积分中心定轨精度分析
根据动力学影响将第一时段和第二时段数据分别进行统计定轨,积分中心为月心,基准轨道采用USB测距与VLBI时延及时延率数据融合定轨的策略,定轨求解策略参考第1节设置。计算的定轨残差如图8所示。
由图8可知,USB测距拟合残差小于5 m,VLBI时延拟合残差小于1 m,时延率拟合残差小于0.5 mm/s。将上述月心轨道计算结果作为基准,然后分析地心轨道的定轨差异及单USB定轨的精度。其中地心轨道计算完毕后转换至月心轨道与基准进行比较,而单USB定轨则是在月心轨道下采用测距+测速的策略计算的星历与基准进行比较,计算结果见图9。

图8 CE5T服务舱地月L2点绕飞定轨残差Fig.8 Orbit determination residual of CE5T circle libration L2 point of Earth-Moon system
最后通过计算重叠弧段星历偏差分析地月L2点绕飞轨道精度,其中第一时段首先计算11月28日至12月7日的轨道,然后计算12月1日至12月11日的轨道,重叠弧段为12月1日15时至12月7日23时,两组轨道定轨策略一致;第二时段首先计算12月11日至12月20日的轨道,然后计算12月15日至12月26日的轨道,重叠弧段为12月15日08时至12月21日14时。上述分析均在月心轨道下计算,重叠弧段星历偏差如图9所示。
图9(a)表示第一时段地心和月心积分中心不同的定轨星历偏差,起始时间为11月28日0时;图9(b)表示第二时段地心和月心积分中心不同的定轨星历偏差,起始时间为12月11日0时;图9(c)表示第一时段USB定轨与精密定轨比较偏差,起始时间为11月28日0时;图9(d)表示第二时段USB定轨与精密定轨比较偏差,起始时间为12月11日0时;图9(e)表示第一时段重叠弧段星历比较偏差,起始时间为12月1日0时;图9(f)表示第二时段重叠弧段星历比较偏差,起始时间为12月15日0时。不同积分中心定轨的偏差约100 m,与重叠弧段星历偏差相当,月心定轨数据拟合精度稍高,这与月心动力学积分中第三体摄动量级相关,但是地心定轨不涉及天体中心转换,计算效率更高。第一时段USB定轨的误差为百米量级,第二时段USB定轨的误差为十米量级,原因是第二时段测站资源相对较多(包括4个USB测站),跟踪弧段相对平衡,对轨道构型约束更好。

图9 CE5T服务舱地月L2点绕飞定轨星历误差Fig.9 Ephemeris position error of CE5T circle libration L2 point of Earth-Moon system
综上所述,服务舱在地月L2绕飞的定轨同样是以弱引力动力学为基础的求解问题,根据不同需求可以选取地心轨道求解或者月心轨道求解,精密定轨精度为百米量级。
3 环月轨道的CE5T定轨
3.1 动力学模型
CE5T服务舱环绕月球飞行后,于2015年2月至3月开展了月球轨道交会对接试验验证,其中包括调相控制,降轨控制和远距离导引控制,根据轨道高度的不同,选取两组具有代表性的轨道进行分析,第一组近圆轨道是2015年3月2日17时至2015年3月3日05时约6圈数据,轨道高度240 km×160 km,第二组降轨轨道是2015年3月5日21时至2015年3月6日02时约3圈数据,轨道高度180 km×15 km,轨道动力学模型参考表4,但重力场阶次采用660阶次(以下简称Gr 660),利用服务舱第一组轨道和第二组轨道分析轨道动力学各摄动项影响,计算结果如图10所示。
图10(a)表示240 km×160 km轨道加速度,图10(b)表示180 km×15 km轨道加速度。由于服务舱3月6日距离月球更近,月球质点和月球非球形摄动影响更加明显。月球质点加速度与引力常数相关,该参数在动力学模型中通常为常数,非球形摄动与重力场模型的精度相关,本文以Gr 660计算的星历为基准,再利用GRAIL重力场100阶次(以下简称Gr100),LP165重力场165阶次(以下简称LP165)和SGM100重力场100阶次(以下简称SGM100)计算的星历与基准进行比较,计算3月3日和3月6日两组轨道的星历误差如图11所示。

图10 CE5T服务舱绕月轨道动力学影响Fig.10 Dynamics influence of CE5T in lunar orbit
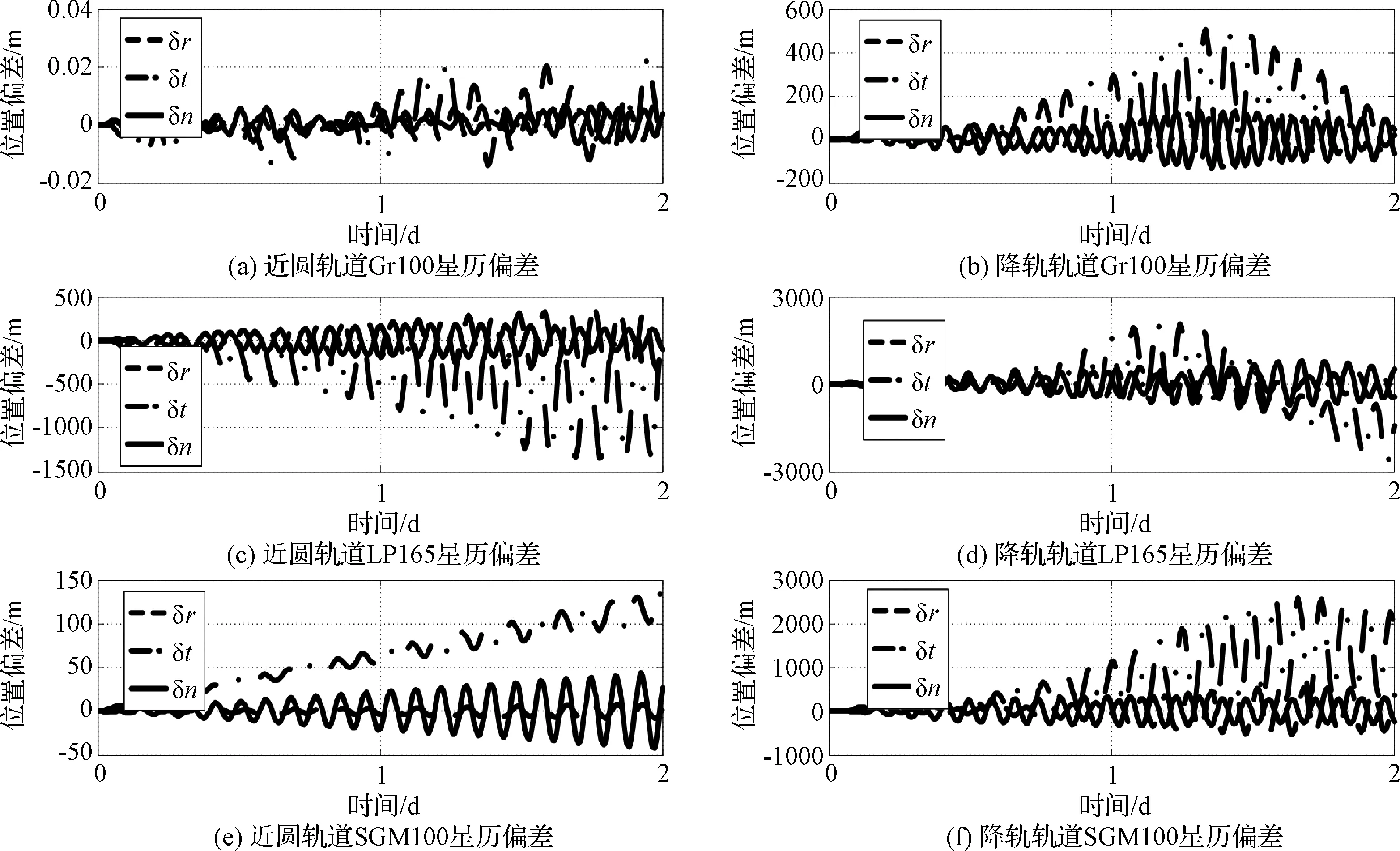
图11 CE5T服务舱绕月轨道星历预报误差Fig.11 Prediction error of CE5T in lunar orbit with difference gravity field
图11为CE5T服务舱绕月轨道星历预报误差。其中,图(a)表示240 km×160 km轨道Gr100计算的星历与基准比较位置偏差(小于0.1 m),图(c)表示LP165计算的星历与基准比较位置偏差(约1.5 km),图(e)表示SGM100计算的星历与基准比较位置偏差(约150 m);图(b)表示180 km×15 km轨道Gr100计算的星历与基准比较位置偏差(约600 m),图(d)表示LP165计算的星历与基准比较位置偏差(约3 km),图(f)表示SGM100计算的星历与基准比较位置偏差(约3 km)。由图可知,对于3月3日较高的轨道,Gr100与基准偏差较小,但是3月6日降轨轨道的偏差达到百米级,使用LP165模型和SGM100模型预报星历偏差达到百米甚至千米量级。下面通过摄动加速度偏差分析重力场影响。

图12 CE5T服务舱绕月轨道非球形摄动加速度偏差Fig.12 Non-spherical acceleration error of CE5T with difference gravity field
图12为CE5T服务舱绕月轨道非球形摄动加速度偏差。其中,图(a)表示240 km×160 km轨道Gr100计算的非球形摄动加速度与基准比较偏差,为10-8m/s2量级,图(c)表示LP165计算结果与基准比较偏差,为10-4m/s2量级,图(e)表示SGM100计算结果与基准比较偏差,为10-6m/s2量级,图(g)表示轨道高度变化;图(b)表示180 km×15 km轨道Gr100计算结果与基准比较偏差,为10-4m/s2量级,图(d)表示LP165计算结果与基准比较偏差,为10-3m/s2量级,图(f)表示SGM100计算结果与基准比较偏差,为10-4m/s2量级,图(h)表示轨道高度变化。由图可知,三种模型与基准比较加速度误差在每一圈都会产生一组极大值(图(e)除外),极大值均发生在近月点处,该误差体现了三种重力场在该轨道上的分辨率。
3.2 基于不同重力场模型的定轨精度分析
根据动力学影响本文将第一时段和第二时段数据分别进行统计定轨,USB站测距每圈设置求解一组系统差,受数据弧段影响,不再求解光压系数。定轨后测量数据拟合统计的均方根(Root mean square,RMS)如表5、表6所示。
JMSSK表示佳木斯深空站,两组轨道均是以Gr660定轨拟合精度最高,其次是Gr100的定轨精度,LP165模型定轨拟合精度超出了测量数据的噪声水平,SGM100模型在近圆轨道的定轨拟合同基准相当,但是在降轨轨道的拟合精度在四组策略中最低。定轨完成后,以Gr660计算星历为基准,然后将其它策略计算星历与之进行比较,统计的误差最大值如表7所示。
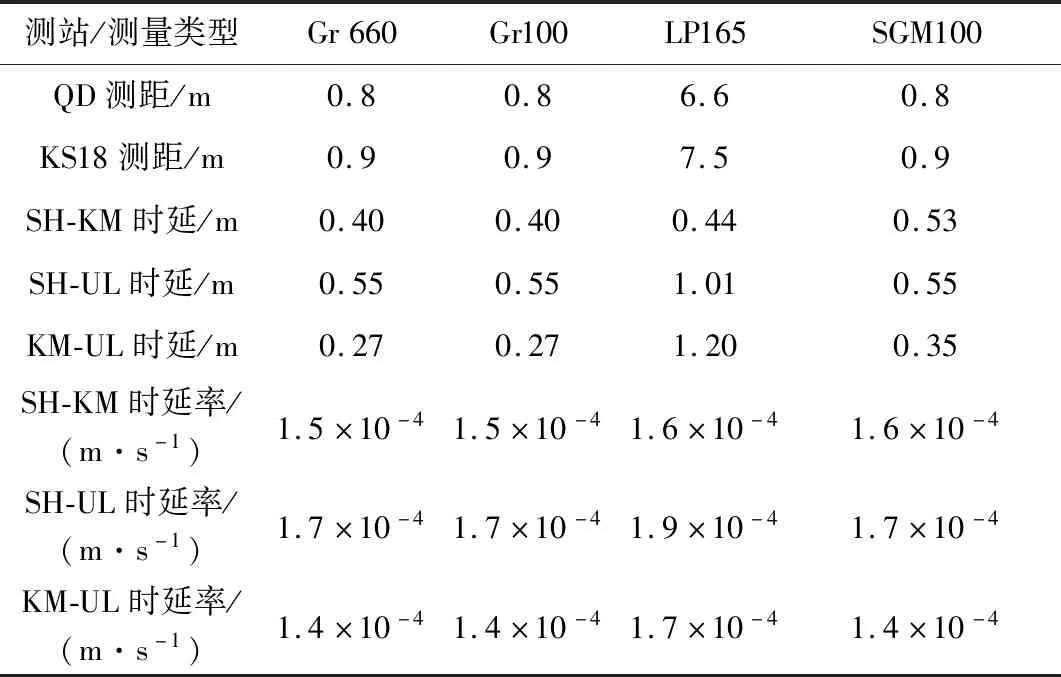
表5 CE5T服务舱绕月近圆轨道定轨数据拟合精度Table 5 Tracking data fitting of lunar near-circular orbit

表6 服务舱绕月降轨轨道定轨数据拟合精度Table 6 Tracking data fitting of lunar lower orbit

表7 CE5T服务舱绕月轨道定轨星历误差Table 7 Ephemeris position error of CE5T in lunar orbit
由表7可知,不同重力场模型导致定轨产生百米级误差,为进一步验证重力场模型精度影响,再使用90°倾角的轨道进行分析,选取CE3探测器在2013年12月7日的100 km×100 km和12月12日的100 km×15 km两组轨道进行计算,定轨策略选取与CE5T服务舱相同,以Gr 660计算星历为基准,然后将其它策略计算星历与之进行比较,统计的误差最大值如表8所示。
由表8可知,在服务舱绕月轨道计算中精度较高的Gr100在降轨轨道中数据拟合精度和星历误差都降低到百米量级,所以Gr100在降轨轨道定轨时,由于模型截断误差不同的轨道倾角影响不同,相反LP165模型在圆轨道和降轨轨道的计算精度均能保持十米量级,因为该模型是月球勘探者卫星在月球90°倾角的轨道反演的,与当前计算轨道的倾角一致,SGM100模型在100 km圆轨道的计算精度约十米,但是在降轨轨道中计算精度降低到百米量级,因为SGM模型采用了月球正面和背面的测量数据,其轨道高度在100 km左右,所以在CE3及CE5T服务舱的近圆轨道计算中精度较高,但受重力场反演时轨道高度的影响,对近月点20 km以下的引力描述与实际存在差异,导致不同倾角的降轨轨道误差均较大。

表8 CE3绕月轨道定轨星历误差Table 8 Ephemeris position error of CE3 in lunar orbit
综上所述,服务舱绕月轨道的定轨建议采用最新的GRAIL重力场模型计算,对于100 km及以上的环月轨道建议截取到100阶次既可以保证计算精度,又可以提高计算效率,因为与660阶次计算时间相比减少30倍,对于近月点20 km以下的环月轨道建议使用660阶次或是适当减少阶次计算。
4 结 论
本文根据CE5T服务舱的拓展试验依次分析了绕地大椭圆轨道、地月L2点绕飞轨道和月球交会对接轨道的定轨精度,其中绕地大椭圆轨道和地月L2点绕飞轨道均属于弱引力条件下的轨道动力学问题,通过不同数据类型组合制定了精密定轨的策略,分析得到绕地大椭圆轨道的定轨精度为百米级,通过分析地心/月心积分及定轨的差异,得到地月L2点绕飞轨道的定轨精度为百米级,其中L2点绕飞的定轨策略可为CE4中继星任务提供支持。针对绕月轨道的动力学特性,选取3类重力场模型对定轨精度的影响进行分析,最大达到了百米量级,建议采用最新的GRAIL模型,结合效率和精度可根据需求截取一定的阶次,计算结果可为CE5交会对接任务提供支持。
