基于自适应模糊PID运动控制系统的设计

何立璐 易映萍 石伟

摘  要： 摘要内容为了提高四轮驱动机器人的速度控制性能和红外循迹轨迹跟踪响应效果，将传统PID控制和模糊推理相结合，设计了一种基于自适应模糊PID的四轮驱动循迹控制系统，介绍了系统总体结构和模糊控制理论，设计了一种自适应模糊PID控制器，给出了以转速为内环，位置偏差为外环的双闭环模糊控制方法，利用simulink对模糊PID算法的控制效果进行了仿真，并在四轮驱动控制系统试验平台上进行速度控制实验和循迹动态响应实验研究，结果表明本文所设计的自适应模糊PID相对于传统PID响应更快，减少系统稳态误差，提高移动平台的红外循迹过程中的轨迹跟踪动态响应效果。

关键词： 四轮驱动;红外循迹;自适应;模糊PID

中图分类号： TP273+.4    文献标识码： A    DOI：10.3969/j.issn.1003-6970.2019.06.002

本文著录格式：何立璐，易映萍，石伟. 基于自适应模糊PID运动控制系统的设计[J]. 软件，2019，40（6）：0712

【Abstract】： In order to improve the speed control performance and infrared tracking response effect of four-wheel drive robot， a tracking control system based on adaptive fuzzy PID is designed by combining traditional PID control with fuzzy reasoning. The overall structure of the system and the theory of fuzzy control are introduced. An adaptive fuzzy PID controller is designed. The speed is the inner loop and the position deviation is the outer loop. The double closed-loop fuzzy control method simulates the control effect of the fuzzy PID algorithm by using simulink， and carries out speed control experiment and track dynamic response experiment on the four-wheel drive control system test platform. The results show that the adaptive fuzzy PID designed in this paper responds faster than the traditional PID， reduces the steady-state error of the system and improves the infrared track passing of the mobile platform. The trajectory tracking dynamic response effect in the process.

【Key words】： Four-wheel drive; Infrared tracking; Adaptive; Fuzzy-PID

0  引言

傳统PID控制器自出现以来，凭借其控制原理简单、稳定性好、工作可靠、易于实现等优点成为工业控制主要技术，常被用于机器人驱动控制。但是传统PID参数整定异常麻烦，当被控对象的结构和参数具有一定的不确定性，无法对其建立精确的模型时，传统PID无法进行实时调节参数[1-2]。对于红外循迹机器人的速度控制系统而言，由于其在循迹过程中为时变非线性系统，不同时刻需要选用不同的PID参数，采用传统的PID控制器，很难使整个运行过程具有较好的运行效果，无法满足控制需求[3]。

为了获得更好的速度控制性能和循迹动态响应，本文将传统PID控制和具有较强鲁棒性能的模糊推理相结合，设计了一种基于自适应模糊PID的移动平台控制系统，设计了一种自适应模糊PID控制器，该算法可根据实际工况对PID参数不断进行模糊化增量调节，实现了移动机器人以转速为内环，位置偏差为外环的双闭环模糊控制。

1  系统总体结构

本系统以四轮驱动为运动模型，结合红外循迹传感器和霍尔测速传感器以及自适应模糊PID控制算法实现的智能移动平台。

1.1  系统介绍

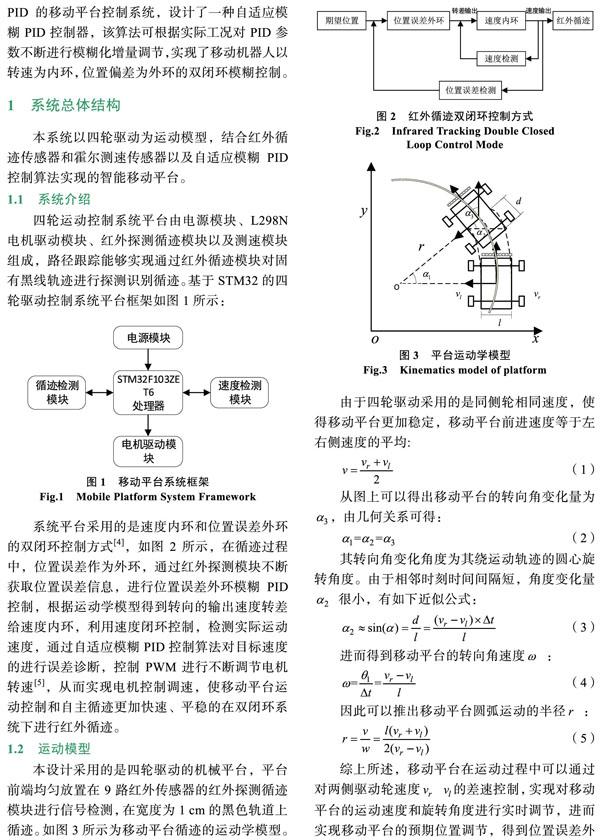
四轮运动控制系统平台由电源模块、L298N电机驱动模块、红外探测循迹模块以及测速模块组成，路径跟踪能够实现通过红外循迹模块对固有黑线轨迹进行探测识别循迹。基于STM32的四轮驱动控制系统平台框架如图1所示：

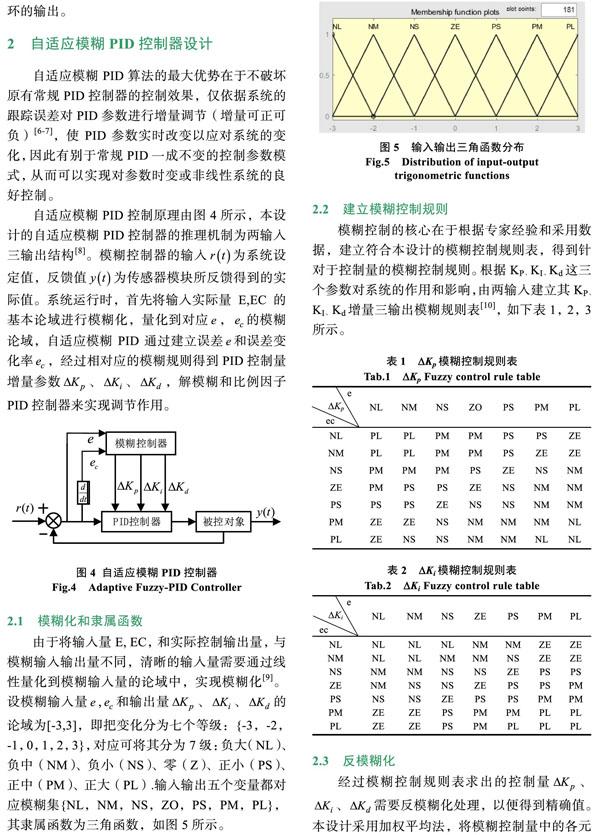
系统平台采用的是速度内环和位置误差外环的双闭环控制方式[4]，如图2所示，在循迹过程中，位置误差作为外环，通过红外探测模块不断获取位置误差信息，进行位置误差外环模糊PID控制，根据运动学模型得到转向的输出速度转差给速度内环，利用速度闭环控制，检测实际运动速度，通过自适应模糊PID控制算法对目标速度的进行误差诊断，控制PWM进行不断调节电机转速[5]，从而实现电机控制调速，使移动平台运动控制和自主循迹更加快速、平稳的在双闭环系统下进行红外循迹。

1.2  运动模型

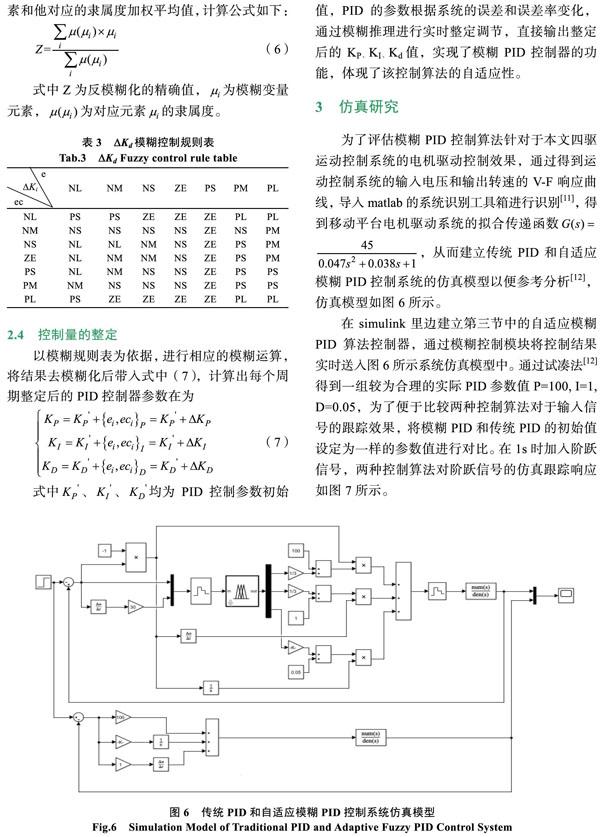
本设计采用的是四轮驱动的机械平台，平台前端均匀放置在9路红外传感器的红外探测循迹模块进行信号检测，在宽度为1 cm的黑色轨道上循迹。如图3所示为移动平台循迹的运动学模型。

综上所述，移动平台在运动过程中可以通过对两侧驱动轮速度   的差速控制，实现对移动平台的运动速度和旋转角度进行实时调节，进而实现移动平台的预期位置调节，得到位置误差外环的输出。

2  自适应模糊PID控制器设计

自适应模糊PID算法的最大优势在于不破坏原有常规PID控制器的控制效果，仅依据系统的跟踪误差对PID参数进行增量调节（增量可正可负）[6-7]，使PID参数实时改变以应对系统的变化，因此有别于常规PID一成不变的控制参数模式，从而可以实现对参数时变或非线性系统的良好控制。

自适应模糊PID控制原理由图4所示，本设计的自适应模糊PID控制器的推理机制为两输入三输出结构[8]。模糊控制器的输入 为系统设定值，反馈值 为传感器模块所反馈得到的实际值。系统运行时，首先将输入实际量E，EC的基本论域进行模糊化，量化到对应 ， 的模糊论域，自适应模糊PID通过建立误差 和误差变化率 ，经过相对应的模糊规则得到PID控制量增量参数 、 、 ，解模糊和比例因子PID控制器来实现调节作用。

2.1  模糊化和隶属函数

由于将输入量E， EC，和实际控制输出量，与模糊输入输出量不同，清晰的输入量需要通过线性量化到模糊输入量的论域中，实现模糊化[9]。设模糊输入量 ， 和输出量 、 、 的论域为[-3，3]，即把变化分为七个等级：{-3，-2，-1，0，1，2，3}，对应可将其分为7级：负大（NL）、负中（NM）、负小（NS）、零（Z）、正小（PS）、正中（PM）、正大（PL）.输入输出五个变量都对应模糊集{NL，NM，NS，ZO，PS，PM，PL}，其隶属函数为三角函数，如图5所示。

2.2  建立模糊控制规则

模糊控制的核心在于根据专家经验和采用数据，建立符合本设计的模糊控制规则表，得到针对于控制量的模糊控制规则。根据KP、KI、Kd这三个参数对系统的作用和影响，由两输入建立其KP、KI、Kd增量三输出模糊规则表[10]，如下表1，2，3所示。

2.3  反模糊化

3  仿真研究

为了评估模糊PID控制算法针对于本文四驱运动控制系统的电机驱动控制效果，通过得到运动控制系统的输入电压和输出转速的V-F响应曲线，导入matlab的系统识别工具箱进行识别[11]，得到移动平台电机驱动系统的拟合传递函数   ，从而建立传统PID和自适应模糊PID控制系统的仿真模型以便参考分析[12]，仿真模型如图6所示。

在simulink里边建立第三节中的自适应模糊PID算法控制器，通过模糊控制模块将控制结果实时送入图6所示系统仿真模型中。通过试凑法[12]得到一组较为合理的实际PID参数值P=100， I=1， D=0.05，为了便于比较两种控制算法对于输入信号的跟踪效果，将模糊PID和传统PID的初始值设定为一样的参数值进行对比。在1s时加入阶跃信号，两种控制算法对阶跃信号的仿真跟踪响应如图7所示。

通过响应曲线和性能指标的对比可得，模糊PID响应的超调量为0.04%，传统PID的超调量为4.5%，在相同控制参数下，自适应模糊PID控制算法相对于传统PID控制可以进行更快的响应跟踪，能有效的减少系统的调节时间和超调量，達到预期效果。

4  实验研究

为了验证实际的控制效果，搭建了四轮驱动控制系统的实验运动平台和相对应的算法程序，系统程序算法流程如图8所示。PID算法均采用的是位置式PID，速度采样周期为250Hz，偏差率的采样时间为500Hz，位置误差采样周期为5kHz，速度内环和位置误差外环的计算周期为5kHz。

4.1  速度内环实验

设定速度偏差E范围为（-1 r/s，1 r/s），速度偏差率Ec范围（-4，4）隶属函数采用三角函数，解模糊采用重心法。根据第三节的参数整定原则，得到速度偏差的量化因子为3，速度偏差的量化因子为3/4，Kp的比例因子为300/3，Ki的比例因子为0.6/3，Kd的比例因子为0.05/3。得到速度内环的模糊PID控制器，设定PID初始值为P=100， I=1， D=0.05的传统PID和模糊PID关于给定速度（1.0 r/s—>0.5r—>0.75r—>1.0r）的速度内环实测动态响应曲线如图所示。

通过速度内环对比试验可以计算出传统PID的速度响应最大超调量为32.6%，响应时间为0.2s，稳态时间为0.8s;模糊PID的速度响应最大超调量为14.9%，响应时间为0.1s，稳态时间为0.6s。由此可以看出在启动过程中以及给定转速突变时，模糊PID控制器相对于传统PID控制器动态响应好，超调小，调节时间短，在不同转速区间有很好的适应能力。

4.2  位置误差外环实验

四轮驱动控制系统试验平台前方装载着9路红外循迹模块，每一路间隔均为1cm，黑色轨道宽度为1cm。故可得到传感器反馈其位置误差状态error的范围为（4cm， 3cm， 2cm， 1cm， 0cm， 1cm， 2cm， 3cm， 4cm），位置误差率即位置误差的切换速率的范围为（-8，8），得到速度偏差的量化因子为3/4，速度偏差的量化因子为3/4，Kp的比例因子为0.4/3，Ki的比例因子为0.0001/3，Kd的比例因子为0.00005/3，得到位置误差外环的模糊控制器，设定PID的初始值为（P=0.4， I=0.0001， D=0.00005），从进行循迹检测到距离黑色轨道最大位置误差-4的直线循迹到期望位置误差为0的动态响应实验，实验如图所示。

通过位置误差外环对比试验可以看出：试验平台从位置最大误差error=-4循迹到期望误差error=0的动态响应时间传统PID为1.95s，模糊PID的动态响应时间为1.72s，模糊PID位置误差外环控制对比于传统PID有11.8%的响应时间提升，使得更快回到误差期望值，具有更好的动态响应性能。

5  结论

本文分析了轮式机器人红外循迹驱动进行路径跟踪循迹时存在的不足和问题，设计了基于模糊PID控制的速度内环转向外环的双闭环控制系统，对系统组织构架和模糊控制算法原理进行了详细阐述。使用simulink搭建的仿真模型以及四轮驱动控制系统试验平台进行仿真和测试，进一步优化算法得到符合实验平台的模糊PID控制参数。结果表明相对于传统PID，模糊PID控制算法在速度内环的控制性能得到有效提高，能有效的减少系统调节时间和超调量，具有更强的稳定性和及时性;在模糊PID速度内环的基础上进行模糊PID的轨迹跟踪实验，实现控制系统试验平台红外循迹路径跟踪，相对比传统PID有效的缩短了响应时间，具有更好的动态响应性能。

参考文献

[1] 揭海宝， 郭清滔， 康积涛， 李平， 谢建， 古树平. 基于模糊自调整PID控制的同步发电机励磁研究[J]. 电力系统保护与控制， 2009， 37（09）： 89-92.

[2] 李瑾鸿. 应用模糊控制原理在差频并网下的自动准同期算法研究[J]. 电力系统保护与控制， 2009， 37（02）： 96-98+105.

[3] 田琦， 李琪， 姚鹏， 赵媛. 基于模糊PID的全方位移动机器人运动控制[J]. 电子科技， 2011， 24（09）： 131-133+139.

[4] 熊中刚， 叶振环， 贺娟， 陈连贵， 令狐金卿. 基于免疫模糊PID的小型农业机械路径智能跟踪控制[J]. 机器人， 2015， 37（02）： 212-223.

[5] 陈政和. 基于Fuzzy-PID的自动泊车车速控制系统的研究[D]. 华南理工大学， 2018.

[6] JIN Junran， HUANG Hengshuo， SUN Junman， et al. Study onfuzzy self-adaptive PID control system of biomass boiler drum water[J]. Journal of Sustainable Bioenergy Systems， 2013， 3（1）： 93-98.

[7] ESFANDYARI M， FANAEI MA， ZOHREIE H. Adaptive fuzzytuning of PID controllers[J]. Neural Computing and Applications， 2013， 23（1）： 19-28.

[8] 支長义， 王瑞玲， 唐道奎， 刘润田. 无刷直流电动机模糊自适应PID控制策略研究[J]. 电力系统保护与控制， 2010， 38（08）： 35-37+42.

[9] 王川川， 赵锦成， 齐晓慧. 模糊控制器设计中量化因子?比例因子的选择[J]. 四川兵工学报， 2009， 30（01）： 61-63.

[10] 邓云伟. 轮式移动机器人运动控制技术研究[D]. 哈尔滨工程大学， 2006.

[11] 陈岚峰， 张亚琴， 程立英， 张志美. 基于数据的MATLAB系统辨识工具箱模型识别[J]. 沈阳师范大学学报（自然科学版）， 2013， 31（04）： 527-530.

[12] 刘金琨. 先进PID控制MATLAB仿真（第4版）[M]. 北京： 电子工业出版社， 2016.