基于字节流信息熵的版面全局复杂度的评估方法
2019-10-08王琪崔荣一
王琪, 崔荣一
( 延边大学 工学院, 吉林 延吉 133002 )
0 引言
随着计算机技术的快速发展和文档数据的日益增加,如何有效管理和使用文档逐渐成为人们关注的问题.版面文档内容复杂度是评价版面内容组成情况的主要指标之一,它有助于人们了解文档的本质属性[1-2]以及分析和处理文档[3]130.传统的版面分析是将版面内容作为一个完整的图像,并通过对版面图像进行划分等处理将文档分割成文字、表格以及图像等元素,以此为后续的纯文本版面分析以及字符识别做准备[4].评估版面图像复杂度时,因所关注的内容不同,其评价方法也有所不同.例如: Peters等利用边缘与灰度级对图像的复杂度进行了评价[5].基于文献[5],高振宇等利用图像的信息熵、纹理以及边缘信息等特征对图像的复杂度进行了分析,并采用等权重系数加权求和的方法对图像的复杂度进行了定量的评估[3]132.Zou等利用图像的纹理特征研究了图像的复杂度,并利用灰度共生矩阵对纹理特征进行了分析[6].上述方法中,研究者或只是对图像进行了定性的描述,或没有考虑各指标间的权重,即没有给出准确、定量的描述方法.
计算机存储的版面文档信息中,包含图像空间分布的像素信息(灰度值或彩色数字化编码)和文字部分的文字编码,即文档的二进制字节流中含有图像和文本的原本信息(像素和字符);因此,对文件字节流的复杂度进行分析可判定版面的全局复杂度.基于此,本文以图文要素构成的word 2003版面存储文档为研究对象,提出一种基于文件字节流信息熵的版面全局复杂度的度量方法,并通过实验验证本文方法的有效性.
1 基于字节流信息熵的版面内容复杂度评估
1.1 文件字节流的信息熵
研究表明,信息熵可用于描述信源平均不确定性[7].本文采取二进制方式读取文件,把不同的字节值视为不同的信源符号(称之为字节符号),然后通过统计文件中各字节符号出现的次数,确定信源符号的概率分布,进而计算出该文件的字节流信息熵H(X).信息熵的计算公式为:
(1)
其中P(ai) (i=1,2,…,q)为字节值为i的字节符号ai(i=1,2,…,q)的先验概率,q为不同字节符号的个数.因1个字节为8位二进制数,故q的值为28=256.式(1)中,字节符号之间是相互独立的,而在实际文档中,因文档内容之间具有一定的依赖性,所以字节之间存在关联性.为了真实地反映字节流信息熵,本文采用二维离散平稳信源的信息熵.在二维离散平稳信源的随机序列(X1,X2,…,Xi,…,Xn)中,只有相邻的两个符号之间具有依赖关系.考虑到相邻字节之间的相关性,将上述随机序列分成每两个符号为一组,以此构成2次扩展信源,其形式为X’=XiXi+1.该信源信息熵的计算公式为:
(2)
其中P(aiaj) (i,j=1,2,…,q)为2次扩展信源输出符号X1X2的联合概率.
在离散平稳有记忆信源中,多个符号间具有相互依赖关系,因此可通过N次扩展信源来计算信源的信息熵,并以此获得平均符号熵.平均符号熵的计算公式为:
(3)
当式(3)中的N足够大时,平均符号熵趋于极限熵.
因式(3)计算出的二进制字节流信息熵能够真实地反映文档(含图像和文字)的统计特性,因此式(3)可以用来度量版面文档的总体复杂度.另外,从香农第一定理可知,该信息熵也能够反映文档可压缩的理论界限.
1.2 基于N次扩展字节符号的字节流信息熵的计算

图1 数据处理示意图
计算字节流信息熵时,首先把文件看成二进制字节流,并设置N个字节缓冲区,用于保存文件中的N个字节.将字节的内容转换为整数,即可获得字节符号的索引值.读取新字节时,首先将缓冲区的内容左移一个字节(如图1所示),然后把新字节存放至缓冲区的末尾字节处,并计算字节符号的新索引值.根据每个索引值,统计字节符号出现的概率,再由公式(3)计算出该文件字节流N次扩展的平均信息熵.
基于N次扩展字节符号的平均信息熵的计算算法如下:
AlgorithmN-BYTE COMENTROPY
Input 版面文档文件
Output 该文件的字节流信息熵entropy
Step 1 测量文件长度并保存至fsize
Step 2 计算N次扩展字节符号集合元素个数:n=28N
Step 3n个字节符号个数计数器symbol[0~n-1]清零:
fori=0 ton-1 do
symbol[i]=0
endfor
Step 4 读入文件前N字节至字节符号缓冲区Nbyte[0~N-1]中
Step 5 计算N次扩展首字节符号的索引index:
index=0
fori=0 toN-1 do
index=index*256+Nbyte[i]
endfor
Step 6N次扩展首字节符号个数增1:
symbol[index]=symbol[index]+1
Step 7 对后续字节统计每一个N次扩展字节符号的出现次数:
while (未遇到文件尾) do
Step 7.1 缓冲区Nbyte内容左移一个字节:
fori=0 toN-1 do
Nbyte[i]=Nbyte[i+1]
endfor
Step 7.2 读入新的字节到缓冲区元素Nbyte[N-1]中
Step 7.3 计算新的N次扩展首字节符号的索引index:
index=0
fori=0 toN-1 do
index=index*256+Nbyte[i]
endfor
Step 7.4N次扩展字节符号个数增1:
symbol[index]=symbol[index]+1
endwhile
Step 8 计算各字节符号出现的概率p[0~n-1]:
fori=0 ton-1 do
p[i]=symbol[i]/(fsize-N+1)
endfor
Step 9 计算并返回信息熵entropy:
entropy=0
fori=0 ton-1 do
entropy=entropy+(-p[i]*logp[i])
endfor
entropy=entropy/N
返回entropy
2 实验结果及分析
2.1 实验文档的构成
实验中,纯图片文档由像素为32×32、640×480、1 024×768、1 280×960、1 600×1 200的图像插入到word 2003文档中构成;纯文本文档由空白页以及2、4、6、8、10、12页的文本构成;混合文档由图文混合的1页文档构成.
2.2 字节流信息熵与复杂度的相关实验
1)扩展级数N的确定.根据香农信息理论,当扩展到一定程度时,平均信息熵将趋近于极限熵,并基本保持不变[7].编程实现上述算法,并通过实验取字节信息熵稳定的N值作为扩展级数.由图2可以看出,采用4,5-byte方式读取文档时,信息熵最小,且通过4,5-byte可以确定图像的信息熵,因此本文取N=4.
2)图像复杂程度与信息熵的关系.图像复杂程度与信息熵的关系实验结果如3图所示,图3中不同的线型表示不同复杂程度的图像.将不同大小的简单图像与真实场景图像(图4)进行对比,结果表明,复杂图像的信息熵明显大于简单图像的信息熵,因此可通过计算信息熵的方法来判断文档中图像的复杂程度.
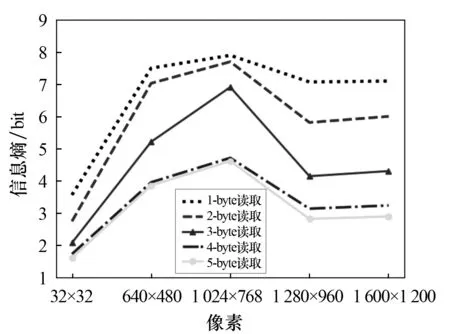
图2 图像像素大小与信息熵的关系

图3 4-byte读取时图像复杂程度与信息熵的关系

(a)画面较为复杂的图像 (b)画面较为简单的图像图4 实验图像
3)文档大小与信息熵的关系.由图5可以看出,文档长度越长,信息熵越大;因此,可采用基于信息熵的方法来评估不同长度文档的复杂程度.采用同一种读取方式时,信息熵越大,说明文档长度越长.
4)文档内容与信息熵的关系.由图6可以看出,采用4-byte方式读取文档时,图文混合文档的信息熵最大,其次为仅含图片的文档,最小的为仅包含文字的文档;因此,在文档篇幅一样的情况下,可以利用信息熵来评估文档的复杂程度.
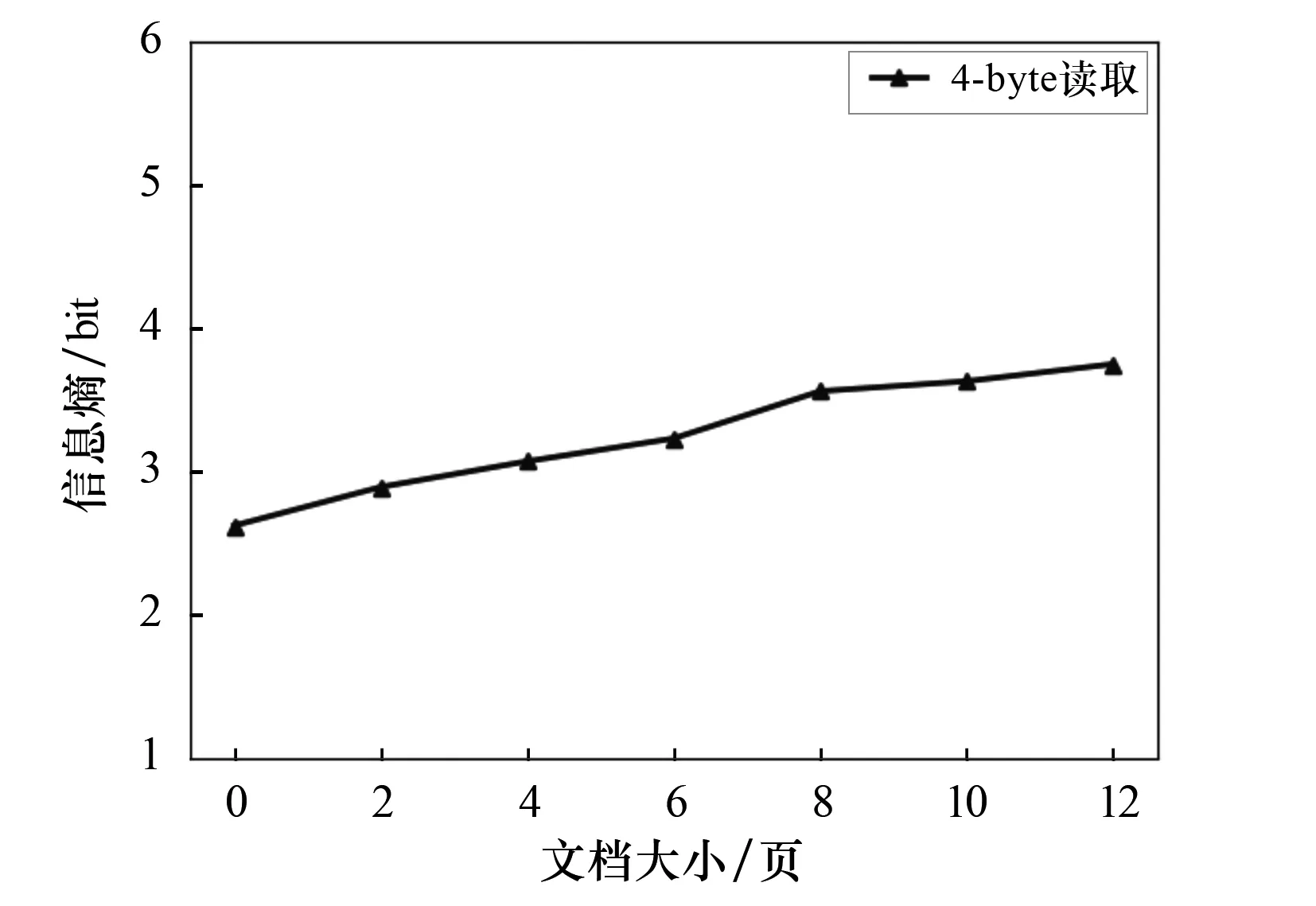
图5 文档大小与信息熵的关系

图6 文档内容与信息熵的关系
上述实验表明:对于同样篇幅的文档,图文混合文档的信息熵最大;文档的长度越长,文档的信息熵越大;对于纯图像文档,画面内容丰富的图像文档的信息熵大于画面简单的图像文档的信息熵.该结果与实际情况相符.
3 结论
本文采用文件字节流信息熵的方法对文档内容进行了复杂度评估,该方法不用对文档中图文进行细节划分即可实现对文档内容复杂程度的评估;因此,本文提出的方法优于传统的版面分析方法,且能够提高文档的分析效率.同时,本文方法也可为文档的可压缩性提供度量.本文在研究中仅考虑了以word 2003为存储格式的文档内容复杂度,今后我们将采用不同的文档格式(如PDF、RTF、TXT等)来测试本文方法的适用性.
