基于差分进化的量子粒子群优化算法的研究

留黎钦， 孙波， 王保云， 张萍

( 1.莆田学院 信息工程学院， 福建 莆田 351100； 2.南京邮电大学 通信与信息工程学院， 江苏 南京 210003 )

0 引言

群体智能算法通过模拟生物种群个体之间的合作、竞争、交互和学习，可以在缺少局部信息的情况下，完成复杂问题求解.目前，群体智能算法已被广泛应用于无线通信系统、神经网络、图像处理、网络态势预测、特征选择、数据聚类等领域，其主要应用的算法有遗传算法、蚁群优化算法、差分进化算法和粒子群优化算法.差分进化算法(differential evolution，DE)[1]是一种全局优化启发式算法，它可通过选择变异的策略和设置相关参数来寻找最优解.差分进化算法具有简单和易于实现的优点，但若迭代次数过多，容易引起过早的局部收敛.粒子群优化算法(PSO)是一种模拟鸟群寻找食物的智能优化算法，该算法易于搜索，收敛速度快[2]，但容易陷入局部最优.为了提高粒子群优化算法的性能， Shi等[3]在粒子群算法中引进惯性权重来平衡局部和全局的搜索，但该算法容易过早收敛，即容易造成局部收敛.Suganthan[4]将粒子群分为若干个小的“邻居群”，通过对每个“邻居群”进行PSO迭代来寻找最优值，该方法虽然不容易陷入局部最优，但计算较为复杂.量子粒子群算法(QPSO)[5]中的粒子处于被束缚状态，它能够通过搜索整个解空间来获得全局最优解，但该算法在收敛过程中会减少种群的多样性.为了提高量子粒子群算法的性能，本文将差分进化的思想引入到量子粒子群算法中，并通过仿真实验证明本文方法的有效性.

1 量子粒子群优化算法

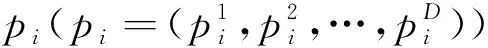
局部吸引点的定义为：

(1)

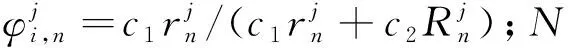
在QPSO算法中，粒子最终收敛在以局部吸引点为中心的δ势阱中，并更新迭代.假设粒子群具有D维的量子空间，粒子群在第n次迭代中，第i个粒子在以局部吸引点pi为中心的δ势阱中移动,则在第n+1次迭代中，粒子状态的更新如下式所示：

(2)

(3)

(4)

在QPSO算法中，最后更新的是粒子个体最优状态pbesti,n+1和群体最优状态gbestn+1， 即:

(5)

(6)

2 差分进化算法

差分进化算法主要包括变异、交叉和选择操作.

1)变异操作.变异操作是将两个个体向量之间的加权差加到第3个向量来产生新的个体，即对n时刻的第i个个体xi,n进行变异操作以产生变异个体vi,n+1[6]，其表达式如下：

(7)

其中，r1,r2,r3∈[1,M],且为互不相同的整数，同时与i均不相等.在变异操作中，xi,n被称为父基向量， (xr2,n-xr3,n)被称为父差分向量，K为比例因子.

2)交叉操作.为了改善种群的多样性，对变异个体vi,n+1按式(8)进行交叉操作，以此产生测试个体ui,n+1.

(8)

其中：CR是交叉概率，介于[0，1]；jrand是一个随机数，满足jrand∈[1,2,3，…，D].该操作可以保证个体至少在一个维度上发生变异.

3)选择操作.由贪婪选择算法确定进入下一次迭代的个体：

(9)

3 基于差分进化的粒子群优化算法(DE-QPSO)

DE-QPSO算法与QPSO算法的不同之处在于在粒子更新过程中引进了DE算法中的变异、交叉和选择操作[7]，具体操作如下：

1)变异操作.当粒子进行状态更新时，添加一个扰动以生成一个变异粒子vi,n+1， 即

(10)

其中F为缩放因子.为了充分利用QPSO算法中粒子全局收敛的优势，在变异操作中不仅保留了QPSO算法中的局部吸引子和δ势阱，还增加了差分向量.通过该方法不仅可以增加扰动，而且可以提高种群的多样性.

2)交叉操作.对由公式(10)产生的变异粒子vi,n+1进行交叉操作，以此产生测试粒子ui,n+1：

(11)

其中：CR是交叉概率，介于(0，1)；jrand是一个随机数，满足jrand∈[1,2,3,…,D].

3)选择操作.DE-QPSO算法的选择操作和DE算法相同，如公式(9)表示.

粒子状态更新结束后，更新粒子个体最优pbesti,n+1和群体最优gbestn+1，其更新过程如公式(5)—(6)所示.

DE -QPSO算法的具体步骤如下：

步骤2 计算平均最优位置Cn，选择合适的α.

步骤3 根据公式(1)计算每个粒子的局部吸引点.

步骤4 根据公式(10)进行变异操作.

步骤5 根据公式(11)进行交叉操作.

步骤6 根据公式(9)进行选择操作.

步骤7 通过目标函数，计算粒子的适应值，并通过式(5)和式(6)更新全局最优gbestn+1和个体最优pbesti,n+1；

步骤8 若不满足收敛条件，则返回步骤2，继续执行；否则，结束算法，输出结果.

4 仿真实验与分析

使用5个标准函数(Rosenbrock函数、Sphere函数、Griewank函数、Rastrigin函数以及Ackley函数)测试DE-QPSO、PSO和QPSO算法的性能.各算法的迭代次数为1 000次，粒子的维度为10，粒子数为40个.利用各函数分别对目标函数求解50次，并求解出各函数的平均最优值和方差.测试结果见表1.由表1可以看出，DE-QPSO算法在5个函数中均获得最优解，而另外两种算法没有获得最优解.由图1可以看出，在不同的测试函数上，DE -QPSO算法在收敛速度和收敛精度上均优于QPSO和PSO算法.这说明，DE -QPSO算法不仅能够保持种群的多样性，而且有较好的收敛速度和收敛精度.

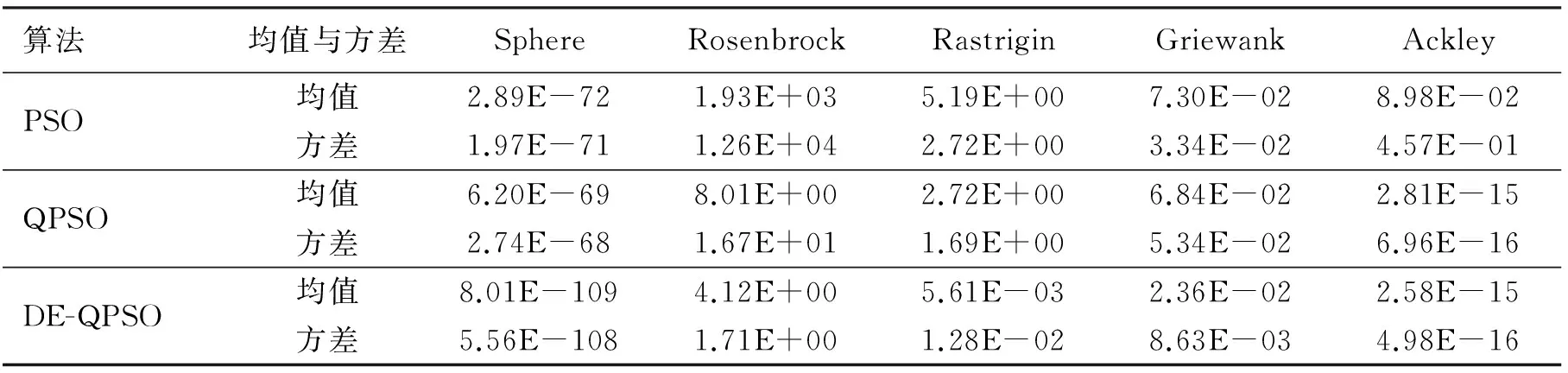
表1 各函数运行50次后的平均最优值和方差

(a) Sphere函数 (b) Rosenbrock函数图1 3种算法在不同标准测试函数上的收敛曲线

4 结论

研究结果表明，本文提出的差分进化量子粒子群算法在5个标准函数(Rosenbrock函数、Sphere函数、Griewank函数、Rastrigin函数以及Ackley函数)中都获得了最优解，且其收敛速度和收敛精度优于PSO和QPSO算法.今后我们将进一步研究DE -QPSO算法在光纤通信信道分配方案问题中的应用.