球杆系统动态仿真实验平台的构建与实现

张 佳，辛 斌，郑荣钦

球杆系统动态仿真实验平台的构建与实现

张 佳，辛 斌，郑荣钦

（北京理工大学 自动化学院 复杂系统智能控制与决策国家重点实验室，北京 100081）

以球杆系统为对象，建立了动态仿真实验平台。结合球杆系统的几何模型和控制系统模型，可进行球杆系统的实时三维动画演示，能够模拟实物球杆系统的运动控制，在仿真实验过程中动态展现实验效果。该平台可用于自动控制和智能控制课程实验教学，便于学生在没有实物实验装置的条件下，不受时间、地点的限制进行仿真实验。该仿真系统具有良好的扩展能力，可以加入多种自动控制与智能控制算法。

球杆系统；仿真实验；PID控制；智能控制

实验教学是理论教学的延伸，有助于学生对知识的消化吸收，在大学教学过程中具有举足轻重的地位。但是，建设实验室花费巨大，实验设备价格昂贵，实验室设备数量有限，使得每个学生实验操作的时间不足，不利于培养学生的创新能力和工程素质。随着信息技术的发展，仿真实验在高校中被广泛应用。它突破了传统实验教学中场地、设备、安全性等因素的制约[1-3]，具有成本低、维护简单、不受时间地点限制、可扩展等优势。

球杆系统具有非线性不稳定系统的所有重要动态特性，是控制类课程教学实验中常用的设备。球杆系统经典的控制算法包括PID控制法[4]、状态空间法[5]、模糊控制法[6]、神经网络控制法[7]等智能控制方法。

现有的基于球杆系统的虚拟仿真平台[8-9]，存在缺乏实物实验装置的动态效果或仿真非实时性等问题。因此，本文以球杆系统为对象，结合Simulink[10]和VC++的优势[11]，开发了具有三维动画演示功能的实时仿真实验平台。验证结果表明仿真实验效果与实物球杆系统上的实验效果一致。该仿真系统能够将球杆系统的运动过程实时呈现给实验者。同时平台具有仿真参数推荐功能，具有指导学生实验作用。

1 球杆系统及其控制系统建模

1.1 球杆系统建模

球杆系统由横杆、小球、支架、伺服电机、齿轮和控制器组成[12]。小球可以沿横杆滚动，横杆可围绕转轴上下摆动。通过直流伺服电机可以控制横杆的倾斜角，使小球在重力作用下沿直杆滚动。球杆系统的物理模型如图1所示。伺服电机转动角度为，横杆上下摆动角度为。

图1 球杆系统物理模型

忽略小球和杆之间的摩擦力，小球的拉格朗日运动方程为

式（1）中为小球半径，为小球质量，为小球转动惯量，为重力加速度。在横杆角度很小或者为0时，对式（1）可做线性化处理：

电机转角和横杆角度的等价关系可表示为[6]：

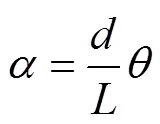
对式（2）进行拉普拉斯变换得到：

因此，以横杆角度为输入，小球位置为输出的系统传递函数为：

将式（3）带入式（5）中，即可得到以转角为输入，小球位置为输出的系统传递函数：

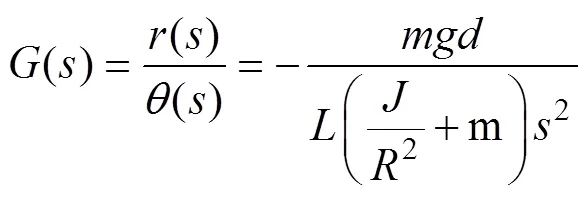
本文球杆系统以固高科技公司的产品GBB1004球杆系统作为参照，设备参数为：=0.11 kg，=0.015 m，=-0.98 m/s2，=0.4 m，=0.04 m，=22/5。

将实物设备参数代入式（6）中，可得式子右边的结果。

球杆系统动力部分采用伺服电机，其电压到转角的传递函数可表示为

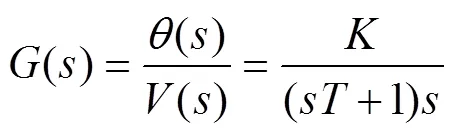
其中：是伺服电机的时间常数，是伺服电机的增益。由于电机的某些参数难以精确测量，并且伺服电机的时间等参数很小，因此，可将伺服电机看作是一个积分环节。

1.2 球杆系统控制系统设计

控制器是球杆系统实验的核心，控制器的好坏直接决定了系统能否稳定以及稳定效果。现有的控制方法很多，例如PID、零极点配置、LQR等经典控制方法，以及模糊控制、神经控制等智能控制方法。本文首先采用经典的PID控制器对球杆系统进行控制，学生只需设置3个参数就可以实现控制。在球杆系统建模分析中，在平衡位置附近对球杆系统进行了线性化处理。PID传递函数为

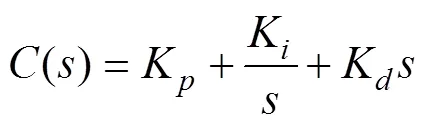
其中：p、i、d分别表示PID的比例、积分和微分单元的参数，通过调节这些参数即可实现对球杆系统的控制。

由建模分析可以看出：球杆系统是一个3阶不稳定系统。对于3阶系统，无法通过一个PID控制器使其稳定。因此，需要对电机和球杆各设计一个控制器，构成双环反馈控制。控制结构如图2所示。

图2 系统控制结构框图

系统输入为小球参考位置，输出为小球实际位置。图2中内环通过PD控制器对电机模型进行闭环控制，外环是对整个系统的PID控制器。将小球实际位置和输入参考位置做比较，其误差作为PID控制器输入。PID输出控制作为电机参考输入，PD控制电机进而控制球杆。

2 仿真模型构建

2.1 球杆系统仿真模型

当横杆在平衡位置附近时，对球杆系统的拉格朗日非线性方程进行了线性化处理，线性化后的方程经过拉普拉斯变换得到球杆系统传递函数，重写传递函数为

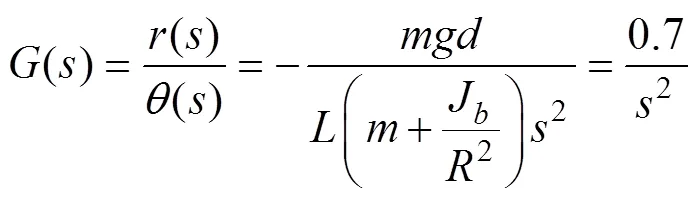
该方程表示小球的位置和伺服电机的转动角度之间的输入/输出关系。将球杆系统的电机参数代入直流伺服电机的数学模型中，得到球杆系统的电机模型

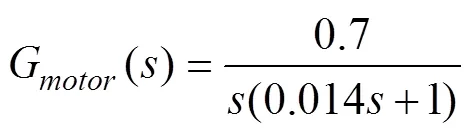
式（11）根据球杆系统实验设备参数得到，符合直流伺服电机的规律，可以近似为积分环节用于系统的仿真。在后续球杆系统的仿真控制过程中，球杆系统及直流伺服电机均采用式（10）和式（11）作为系统的仿真模型。

2.2 球杆系统动画模型

球杆系统动画模型用于实时动态显示实验效果。应用OpenGL[13]开发了球杆系统的三维动画模型，模型的各部件尺寸比例按照真实球杆系统实验装置各部件的比例设置。

球杆系统的三维动画模型对支架、横杆、小球以及齿轮等几个主体部分进行了绘制。横杆采用长方体表示，模型支架由2个不同形状的长方体构成，齿轮采用圆盘表示，各元件之间连接转轴采用小圆柱替代。此外，模型中对小球的运动范围作了限制，使其只能在横杆的长度范围内滚动。

为了便于观察球杆系统三维动画模型的仿真效果，通过OpenGL键盘消息处理函数实现模型任意视角的切换，例如左侧视、右侧视角和正面视角。球杆系统三维动画模型设置有2个接口，分别是齿轮转角和小球在横杆上的位置。系统通过这两个接口即可实现球杆动画模型对实物球杆系统装置运动效果的模拟功能。

3 仿真参数推荐功能设计

在参数整定过程中，实验者往往因对系统理解不够深入或者缺乏调试经验而无从下手。为此，本文通过K近邻算法实现了球杆系统控制参数的推荐功能。根据用户的输入和期望指标，向实验者推荐合适的比例、积分及微分参数，帮助用户实现对球杆系统的稳定控制，并达到指定的控制效果。

K近邻算法的思想是：如果一个样本在特征空间中的个最相邻的样本中的大多数属于某一个类别，则该样本也属于这个类别，并具有这个类别样本的特性。以PID控制方法为例，假设基于PID控制器的球杆系统有两组相似的控制效果，可以认为它们是在相似的PID控制参数下得到的控制效果。用近邻算法在训练集中找出具有相同或相似控制效果的样本实例，将其控制参数作为推荐参数。

在参数推荐模块，期望达到的控制效果即为控制参数推荐模块的输入，包括小球位置ref、上升时间t、峰值时间p、调整时间a、达到10%目标值的时间t_10、达到90%目标值的时间t_90、峰值valmax、超调量，以及稳态误差等指标。输出为PID控制器的参数，包括球杆系统外环PID控制器的比例系数p、积分系数i、微分系数d，以及内环PD控制器的比例系数mkp和微分系数mkd。给定推荐实例，即期望达到的控制效果，得到个最近邻，推荐组PID控制参数。表1、表2分别为实例中，PID控制参数推荐模块的输入、输出样例。

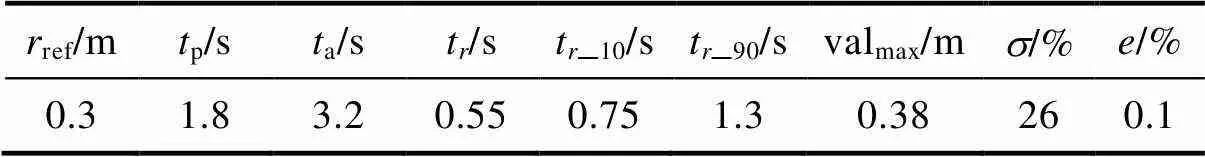
表1 PID参数推荐模块输入

表2 PID控制器参数推荐结果

表2中推荐结果按照与样例的相似程度排序。可以看出，具有相似仿真结果的控制器，其参数具有一定的相似性，普遍存在积分系数较小、电机比例系数较大的情况。将表2中的参数代入球杆系统的控制器中，得到仿真曲线如图3所示。

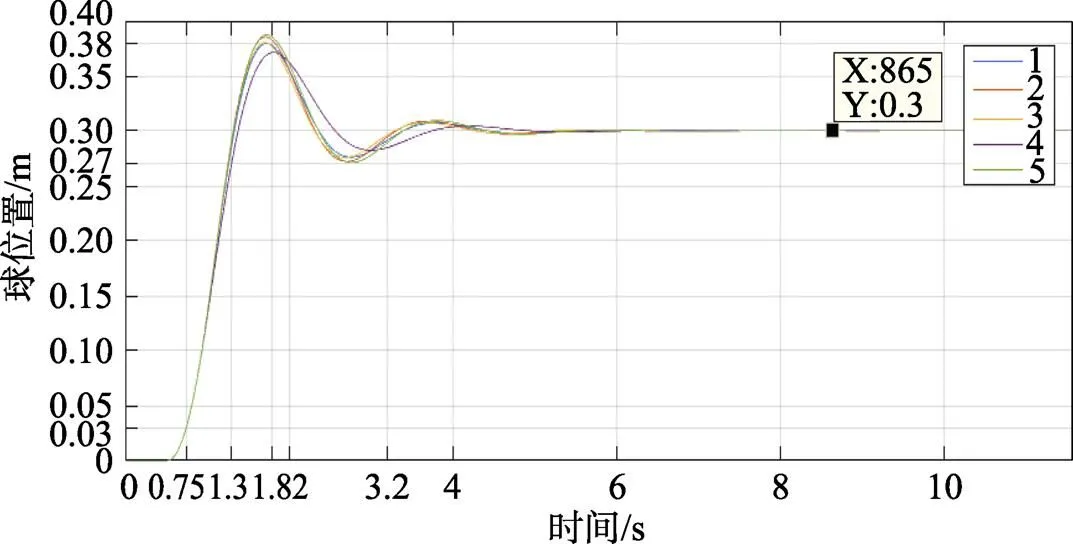
图3 多组PID推荐参数的仿真结果

从图3可以看出，在K近邻算法推荐的5组PID控制参数的作用下，球杆系统均可以实现稳定控制，且控制效果相似。距离越近，得到的控制效果就越接近表1中要求的控制效果。当小球的位置响应曲线在0.75 s时达到目标值的10%，在1.3 s之前达到目标值的90%，在1.8 s之前达到峰值，峰值为0.38 m，稳态误差小于0.1%，达到了期望的控制效果。由此可见，基于K近邻的算法可以实现PID控制器参数的推荐功能。

4 仿真实验平台的设计与实现

4.1 系统框架设计

系统框架设计中，将系统的各个模块分成界面层部分和后台功能部分进行设计。系统整体框架如图4所示。

图4 系统整体框架

从图4中可以看出，上层界面层包含算法选择及其参数设置、算法理论学习、三维动画演示、仿真算法参数推荐以及仿真数据波形显示几个模块。后台运行层包含球杆系统仿真模块和算法参数推荐计算模块两部分。系统上层交互界面和后台功能模块之间通过数据管理模块进行通信。

4.2 软件实现

球杆系统仿真实验平台的交互界面在Microsoft Visual C++环境中进行开发。由于上层界面的功能模块较多，因此仿真实验平台的界面采用VC++单文档多视图结构设计，具有设置控制器参数、仿真时间、小球位置初始等功能，同时需要实时进行仿真波形的显示和三维动画的演示。

后台运行层将Matlab作为后台计算引擎实现。交互界面层的算法参数、系统设置数据等通过Matlab工作空间传递至后台球杆系统仿真模型。同理，后台运行层中的球杆系统仿真模型在完成仿真之后，将仿真数据通过Matlab工作空间传递交互界面显示。

4.3 仿真平台和球杆实验装置效果对比

以经典PID控制方法为例，在所开发的仿真实验平台与实际球杆系统实验装置上采用相同的控制参数，以便进行实验效果的比较。

在相同的系统阶跃输入下，阶跃输入的大小为0.15，阶跃时间为2.5 s，仿真时间为30 s。仿真实验平台和球杆系统实验装置的阶跃响应如图5所示。

从图5可以看出，在相同的控制器、控制参数以及阶跃输入下，仿真实验平台与球杆实验装置的响应曲线在超调量、稳定时间以及稳定输出等方面基本一致。但由于仿真环境是理想环境，不存在实验装置中噪声干扰和精确度等问题，因而仿真平台的阶跃响应曲线更理想。为了更好地模拟实物球杆系统装置的运动效果，在仿真过程中，系统可以有选择地加入噪声，模拟真实实验环境中的干扰，使三维动画模型在演示球杆系统平衡位置的运动时，动态效果更明显且逼真。在球杆系统PID控制仿真模型中加入白噪声后阶跃响应曲线如图6所示。

图5 仿真实验平台及实验装置的阶跃响应比较

图6 带噪声仿真实验平台阶跃响应

从图6可以看出，仿真平台加入白噪声之后，其阶跃响应曲线更接近真实球杆系统实验装置响应曲线。这种情况下，三维动画模型的在平衡位置附近会有类似于实验装置受到干扰时的抖动现象。

仿真过程中几何模型的运动和波形图绘画都与球杆仿真模型同步进行。从图5可以看出系统可以较快地达到稳定。在实物球杆系统中，为防止系统失控，对横杆转动角度有所限制。因此，本系统中将横杆的转动角度限制在±10°范围内。

5 结论

开发的球杆系统仿真实验平台可作为控制类课程相关配套实验平台使用，使学生不受时间、地点的限制，通过球杆系统仿真实验的三维动画，观察到与实物球杆系统相同的运动情况，达到与操作实物球杆系统同样的实验效果。平台的仿真参数推荐功能可有效提高实验效率，指导学生进行实验操作。该仿真平台具有良好扩展性，可以采用自动控制、智能控制等方法控制球杆系统，因此可以用于“自动控制原理”“智能控制”等课程的实验教学。

[1] 万桂怡，崔建军，张振果.高校虚拟实验平台的设计及实践[J].实验室研究与探索，2011, 30(3): 386–389.

[2] Torre L D L, Guinaldo M, Heradio R, et al. The Ball and Beam System: A Case Study of Virtual and Remote Lab Enhancement With Moodle[J]. IEEE Transactions on Industrial Informatics, 2015, 11(4): 934–945.

[3] 白瑞峰，韩洪洪，于赫洋，等.智能制造虚拟实验系统设计与集成[J].实验技术与管理，2016, 33(6): 129–131, 149.

[4] FUAAD M, WAHID H, WAHAB N A. Application of Intelligent Controller in a Ball and Beam Control System[J]. International Journal on Smart Sensing and Intelligent Systems, 2010,3(1): 45–60.

[5] 许冬兰，李玉强.基于状态空间法的海洋生态环境承载力评价[J].统计与决策，2013(18): 58–60.

[6] AMJAD M, KASHIF M I, ABDULLAH S S, et al. Fuzzy Logic Control of Ball and Beam System[C]//2010 2nd International Conference on Education Technology and Computer (ICETC 2010), 2010: 489–493.

[7] WEI Wei, PENG Xue. A Research on Control Methods of Ball and Beam System Based on Adaptive Neural Network[C]// Proceedings 2010 International Conference on Computational and Information Sciences (ICCIS 2010), 2010: 1072–1075.

[8] PAN Feng, CHEN Dali, DA-ZHI E, et al. The Real-Time Simulation of Ball-Beam System based on dSPACE[C]. //2008 Chinese Control and Decision Conference (CCDC), 2008: 221–224.

[9] 杨振华，何岭松.基于Matlab和OpenGL球杆系统虚拟仿真[J].实验技术与管理，2010, 27(4): 83–86.

[10] 孙忠潇，Simulink仿真及代码生成技术入门到精通[M].北京：北京航空航天大学出版社，2015.

[11] 侯晓波，左文英.基于Simulink与VC混合编程方法的研究与应用[J].自动化技术与应用，2010, 29(11): 29–32.

[12] KESHMIRI M, JAHROMI A F, MOHEBBI A, et al.Modeling and Control of Ball and Beam System Using Model Based and Non-model Based Control Approaches[J]. International Journal on Smart Sensing and Intelligent Systems, 2012, 5(1): 14–35.

[13] 韩样.基于OpenGL的三维地形可视化方法研究[J].车辆与动力技术，2003(2): 11–15.

Construction and realization of dynamic simulation platform based on ball and rod system

ZHANG Jia, XIN Bin, ZHENG Rongqin

(Key Laboratory of Intelligent Control and Decision of Complex System, School of Automation, Beijing Institute of Technology, Beijing 100081, China)

A dynamic simulation experiment platform for the ball and rod system is established. In combination with the geometric model and the control system model of the ball and rod system, the real-time 3D animation demonstration of the ball and rod system can be carried out, and the motion control of the real ball and rod system can be simulated. In the process of the simulation experiment, the experimental results are dynamically shown. This platform can be used in the experiment teaching for the automatic control and intelligent control courses, and it is convenient for students to carry out simulation experiments without physical experimental devices and without limitations of time and place. The simulation system has good expansibility and can add many kinds of automatic control and intelligent control algorithms.

ball and rod system; simulation experiment; PID control; intelligent control

TP273

A

1002-4956(2019)07-0120-04

10.16791/j.cnki.sjg.2019.07.029

2018-09-19

复杂系统智能控制与决策国家重点实验室资助

张佳（1980—），女，北京，博士，高级实验师，主要研究方向为智能信息处理.E-mail: zhangjia@bit.edu.cn