一种基于改进置信度传播的个性化推荐算法∗

龚 安 孙育红

（中国石油大学（华东）计算机与通信工程学院 青岛 266580）

1 引言

随着电子商务的广泛普及，推荐系统获得了极大的发展并且已经应用于生活的方方面面。推荐算法是推荐系统的核心，目前常用的推荐算法有协同过滤推荐［1］、基于知识的推荐［2］、基于内容的推荐［3］、基于图模型的推荐［4］及混合推荐［5］等。这些推荐算法通过预测用户对项目的评分来推荐项目给用户并且已经在各自相应的文献中证明了其有效性。然而在某些情况下，比如在为顾客推荐商品时，应该挑选出特定数量的商品并将其排列顺序给顾客，尤其在网上购物时，一个包含特定数量商品的排名列表更受顾客欢迎。这类情况下，项目的排名被认为要比预测用户对项目的评分更重要。因此研究找到排名前n位的项目推荐即TOP-N推荐［6～7］而不是单纯预测用户对项目的评分是很有必要的。

基于RWR的方法［8～9］就是一种TOP-N推荐，它将概率统计模型中的随机游走算法引入到个性化推荐中，通过计算项目集和用户集的用户-项目排序矩阵来计算用户对项目的偏好程度，在评估排名结果度量上明显要优于传统的协同过滤算法。文献［10］在随机游走算法的基础上进行了改进优化，提出了一种基于项目-标签导向的随机游走推荐模型，在一定程度上消减了数据稀疏性问题和冷启动问题。文献［11～12］也对该算法进行了不同的改进优化，有效地提高了精确度和项目的多样性。然而，上述算法都只考虑了马尔科夫场中均匀的结点却未考虑异相的结点，一定程度上影响了推荐结果的精度，并且这些算法在矩阵分解时消耗的空间代价极大。

针对上述问题，将置信度传播算法（Belief Propagation，BP）［13］引入到推荐系统中隐式地挖掘用户对项目的偏好，BP算法利用信息在马尔科夫场中结点间的传递来计算目标结点的置信度，将其引入TOP-N推荐系统能避免上述问题。另外，考虑到BP算法在计算置信度时采用全局的结点，有较大的冗余计算，因此先将其优化改进，采用自适应大小区域内的结点计算置信度，然后引入推荐系统［14～15］建立新模型:将用户集和项目集作为两个结点集合建立二分图，用户对项目的评分作为用户结点和项目结点的边缘阈值，通过置信度在项目结点和用户结点之间的传递来迭代计算目标结点置信度，根据最终置信度大小生成排名列表。通过实验发现，改进后的BP算法在不损失精度的前提下，效率远高于传统BP算法，并且在Precision值和Recall值和MAP值三方面均优于协同过滤算法和基于RWR的方法。

2 BP算法

置信度传播算法是基于马尔科夫随机场的一种近似计算，马尔科夫场中的结点是成对的，分为隐式和显式两个状态。置信度传播算法利用迭代的算法在结点与结点之间传递信息，从而利用这些信息及当前结点的状态来推断相邻结点的状态，进而更新当前整个马尔科夫场的标记状态，它可以解决概率图模型的概率推断问题，且所有问题并行实现，多次迭代后，所有结点的置信度不再发生变化，达到最优状态，此时的马尔科夫场也达到收敛状态。

马尔科夫场的两个关键过程:

1）加权乘积计算所有结点信息；

2）信息在随机场中的传递。

一个结点到另一个结点传递的信息叫做信息向量，向量中元素的个数等于该结点可能所处的状态数目。信息向量的计算由式（1）获得:

其中，mij(X)表示结点i传递给结点j的消息，表示在 X 状态下，i对j的置信度。N（j）i表示结点 j的MRF一阶邻域中不包含结点i的邻域。Φi(Y)表示结点i处于Y状态下的结点势能。Ψij(Y,X)表示当j的邻结点i处于Y状态时j处于X状态的概率，由传播矩阵获得，传播矩阵在4.3节中给出。

图1演示信息传递过程。

图1 信息传递机制

此时，结点i处于状态X的置信度为式（2）所示:

其中，k是归一化因子，最终的置信度代表结点处于相应状态的可能性。

3 改进BP算法

在计算目标结点的置信度时传统BP算法考虑了整个马尔科夫场中所有结点对当前结点的影响，运算效率低，而如果只考虑以该结点为中心，自适应大小的区域内结点对目标结点的影响，则可以大大降低时间复杂度，从而提高算法效率。

信息在整个马尔科夫场各结点之间传递时，结点之间相互的影响因结点与目标结点距离而存在差异，与目标结点距离较近的结点可能对目标结点影响较强，距离较远的结点可能影响较弱，所以以目标结点为中心，考虑不同大小区域半径内的结点对目标结点的影响，结果如图2所示。

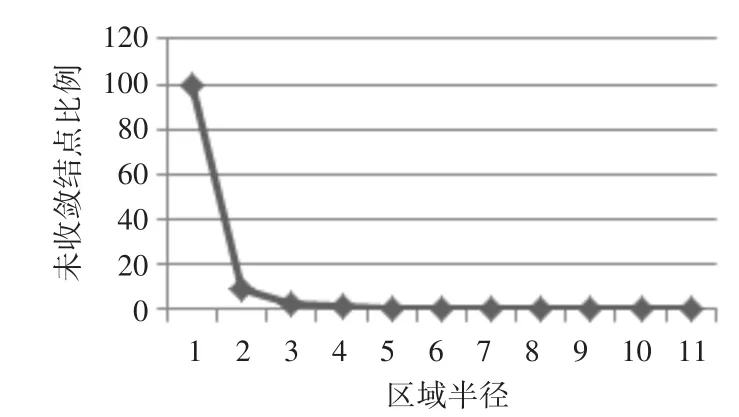
图2 未收敛结点比例示意图

由图2可看出BP算法在马尔科夫随机场中不同区域半径下的结点收敛情况。假设区域半径为r，即只考虑与目标结点距离小于等于r的结点，该区域内所有结点对目标结点传递信息后后者的置信度为mr，同时假设传统BP算法所对应的区域半径为l，即r充分大的情况下，该区域内所有结点对目标的置信度为 ml，r=1，2，…，l，设定阈值 ε，当‖mr-ml‖＜ε时即可认为是收敛。由图2可知，每一个结点只需较小区域内的置信度更新即可收敛，所以自适应区域大小的算法可以有效减少传统BP算法中的冗余计算，所以仅更新未收敛结点的置信度信息，即当‖mr- ml‖＜ε时，认为已经达到收敛状态，此时不再扩大置信度的更新范围。ε的取值在4.4节中给出。

4 基于改进BP算法的个性化推荐算法

4.1 二分图模型的建立

创建一个用户关于项目偏好的二分图，将用户集合和项目集合作为两个结点集合，建立二分图。结点的状态分为喜欢和不喜欢两个状态。为了提高准确度，设定当评分高于某个阈值时认为用户喜欢该项目，否则认为不喜欢该项目，当评分高于这个阈值时建立用户结点和该项目结点的边，阈值的选择在5.1节中给出。

4.2 结点势能的计算

结点势能是基于项目评分的。因为设定了两种状态:喜欢和不喜欢，所以结点势能也有两种，每个结点势能需分配0.1～0.9之间的某个值，并且一个结点的两个结点势能的和应该为1。目标用户的评分越高，在喜欢状态下的结点势能就越大。结点势能由式（3）获得:

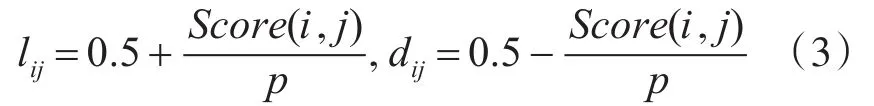
其中，lij表示喜欢状态下的结点势能，dij表示不喜欢状态下的结点势能，Score(i,j)表示目标用户i对项j的评分。常数p是归一化因子。如果获得的结点势能低于0.1或高于0.9，用0.1或0.9代替。未被评分项目的结点势能初始化时在两种状态下均分配为0.5。

4.3 传播矩阵的建立

两结点间势函数值Ψij（Y，X）由传播矩阵获得，表示当j的邻结点i处于Y状态时j处于X状态的概率。在推荐算法中，将两个状态分别设定为喜欢和不喜欢，表1是一个传播矩阵的例子，为避免数字下溢，α设定为一个很小的值。

表1 传播矩阵示例

4.4 置信度消息的更新

大部分马尔科夫场中的结点在受到其某一邻域范围内结点的信息传递后其置信度是趋于收敛的，改进BP算法仅更新尚未收敛结点的置信度而忽略这些收敛结点。因此在计算置信度过程中无需计算整个马尔科夫场中所有结点的置信度，而只要在计算前对结点进行收敛判断，若收敛，则不用计算，若不收敛，则迭代计算其置信度。收敛阈值的选取就显得尤为重要。如果选取阈值过大，一些尚未收敛的结点会被错误判定为收敛结点而停止计算，导致计算结果精度降低；如果选取阈值过小，因为在每次更新置信度时都需要判断是否收敛，所以会增加计算量，而不能有效提高算法效率。综上所述，选择合理的阈值是非常必要的。

为了降低实验复杂度，对‖mr- ml‖＜ε稍作修改，改为判定每个结点在相邻两次信息传递后的误差值小于某个特定阈值，即‖bi+1(X)-bi(X)‖＜ω，经过多次实验验证当ω=1和ω=2时，该算法最优，在实验部分给出说明。在迭代计算完成后，根据最终置信度大小排名生成列表，选取TOP-N项目列表推荐给目标用户。

5 实验和结果分析

实验数据是由美国明尼苏达大学GroupLeans项目提供的开源MovieLens数据集，包含72000名用户对10000部电影的1000万条评分数据，对电影的评分取1～5之间的整数值，从中选取了包含943个用户对1682个电影的10000条评分数据进行实验。实验数据划分为训练集和测试集，训练集和测试集的比例为4∶1，传播矩阵中α的取值为0.0001。

5.1 边缘阈值

在实验数据集中，用户对项目的评分值是1到5之间的整数，所以需在该区域内选取值作为结点与结点之间边缘阈值，为了在实验中得到更精确的结果，考虑1和5之间（不包含1和5）的整数以及评分的算术平均值和几何平均值（GM）作为边缘阈值进行实验观察其各项评测指标，实验结果如表2所示。

表2 不同边缘阈值下性能比较

上述实验为传统BP算法实验结果，这是因为，对于改进BP算法或者传统BP算法，阈值的选择是可以一致的，从表2可以看出，边缘阈值取算术平均值和几何平均值的结果最好，相比之下选取算术平均值作为边缘阈值。

5.2 ω的选择

将传统BP算法和参数ω=1，2的改进BP算法的运算时间做对比，即在不同区域半径下对比三种算法的运算时间，实验结果如表3所示。

从表3中可以看出:随着区域半径的变大，BP算法的运算时间呈线性增长，而改进BP算法的运算时间增长较缓；ω=2的改进BP算法表现效果更好一些（下文均用ω=2的改进BP算法）。

表3 不同半径区域下的各算法运算时间比较

5.3 与传统BP算法的性能比较

将改进BP算法应用到推荐系统后与传统BP算法性能比较，实验结果如表4所示。

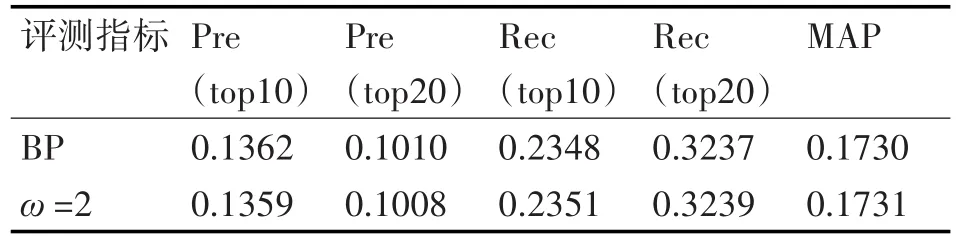
表4 与传统BP算法的性能比较

从表4可以看出，考虑全局结点的传统BP算法与改进BP算法在各项性能指标中并无明显差别，但是结合表3可知，在运算时间上后者明显优于前者。

5.4 不同推荐算法的性能比较

将基于项目的协同过滤算法中的参数k设置为30，此时该算法的精确度能达到最优。对于基于RWR的方法，将高于用户平均评分的评分设为边缘阈值，给目标用户的重启向量元素设为1，其他用户的设为0，重启概率设为0.15，三种算法在精确度、召回率和MAP值指标的比较如图3所示。

图3 不同推荐算法的性能比较

由图3可看出，基于RWR的方法在精确度、召回率和MAP值三个指标上均远高于基于项目的算法，这是因为基于RWR的方法采用迭代随机游走，能够推断结点之间的隐式关系。这也是基于项目的算法的一个缺陷。而改进BP算法要优于基于RWR的方法，因为后者只考虑均匀的结点，而BP同时考虑了均匀和异相［16］。另一方面，改进BP算法既计算了目标用户偏好结点的可能性，也计算了不喜欢结点的可能性。因此，基于改进BP算法的推荐算法优于基于项目的协同过滤算法和基于RWR的方法。

6 结语

将概率统计中的置信度传播算法改进优化后引入到个性化推荐系统中建立了新的推荐模型，把用户集合和项目集合分别作为结点集合建立二分图，通过置信度在马尔科夫场中的传递规律来获取用户的偏好，然后根据最终置信度大小排名生成了一个推荐列表给用户。用自适应大小区域内的结点计算目标结点置信度，比传统BP算法运算时间更少，同时避免了基于RWR的方法存在的一些不足，又不失推荐项目的多样性。通过实验将提出的算法分别与传统BP算法、基于项目的算法和基于RWR的方法做比较，结果表明，提出的算法在各项评测指标方面表现更好，是一种有效的算法。