教学楼内人员应急疏散模型和优化研究
2019-10-06牛智越张亚芳
牛智越 张亚芳


摘 要:针对教学楼内人员的紧急疏散问题,在合理的假设下,对人员的疏散方式进行确定,而后建立了以总疏散时间最小为目标的疏散模型,最后以某高校教学楼为例,运用MATLAB编程求得目标最优值,通过分析变量对目标值的影响,针对影响较大的变量进行优化,并在相关方面提出几点建议。
关键词:教学楼;紧急疏散模型;优化方法
中图分类号:TB 文献标识码:Adoi:10.19311/j.cnki.1672-3198.2019.26.109
1 引言
随着经济的快速发展,人们的物质生活越来越丰富,但同时也带来更多的事故风险,据统计2017年我国中小学校园设施安全事故共发生达64起。而教学楼是校园内建筑规模大,学生高度集中的场地之一。随着学校招生人数的不断扩增,基础设施建设相对落后,教学楼的安全隐患也日益突出,一旦发生紧急事故,要在尽可能短的时间内把学生疏散,必须要有最佳的组织疏散方案,来缩短逃生时间,降低不必要的损失。因此对教学楼内的人员紧急疏散的研究十分必要。
从2010年开始,从不同角度研究紧急疏散的学者越来越多,在基于计算机仿真方面,张涛等在对大型教学楼紧急疏散仿真模拟研究时,利用pathfinder软件对大型教学楼几种情形进行建模仿真,得出制定路线和保持教室后门敞开对人员疏散有极大帮助。赵宜宾等通过建立模型,然后应用元胞自动机来模拟仿真个体在紧急疏散时的行为。在基于数学模型方面,王卫华,朱江等在建筑物人员疏散方案的数学模型研究中,从微观层面考虑人流速度与人流密度关系的数学模型,提出了相应的优化方案。
以上论文虽然从微观层面考虑了人的行为及疏散速度,但是很少从整体角度考虑疏散的总时间最少需要优化哪方面的问题。本文通过建立以总疏散时间最小为目标的疏散模型,来求出总体疏散的最短时间,找出对目标值的影响最敏感的变量,从而对教学楼应急疏散提出建议。
2 问题描述
已知某高校教学楼共有m层,每层有n个通道,且每层布局一致。其中每层楼的所有教室内的人数为pi。其中一楼教室是用来存放设备等其它用途,上课的教室较少。假设现在有紧急事故发生,要求所有人员全部撤离教学楼,如何撤离才能使时间t最短。
由于疏散问题十分复杂,涉及人的心理和生理素质等难以量化把握的因素,为了简化问题,做出以下假设:
(1)假设1楼人员可以迅速离开教学楼,不影响整体的疏散。
(2)假设所有人员能按照既定的线路疏散,不会更换线路。
(3)假设疏散人员到达1楼,就不会再发生拥堵,视为离开教学楼。
(4)假设人流在楼梯上形成最大疏散流后趋于稳态,为楼梯的最大通行能力。
(5)每层楼梯的通行能力不变。
基于以上假设,考虑总疏散时间最短,我们将整个疏散方式确定为:所有楼层人员同时接到疏散指令,按各楼梯的通行能力分配到各个楼梯,从每层距离楼梯口最近的教室开始,到全部疏散完成,分为三个阶段:①教室内人员听到指令后,开始行动,第一个人员到教室门口;②第一个人员从教室口经过走廊与楼梯到达下一层;③之后形成不间断的最大疏散流,所有人员按照指定线路疏散完成。
3 建立模型
为了建立数学模型,定义如下符号和变量。
教学楼紧急疏散问题的数学模型可以表示为如下模型。
目标函数(1)表示整个疏散过程的时间,约束条件;(2)表示每层的楼梯按自身的通行能力来分配疏散每层的人员,约束条件;(3)表示2层各楼梯在tj时间内疏散的总人数至少多于各层对应楼梯疏散各自楼层人员的总和,约束条件;(4)中q*的取值参考文献中的最大通量,其对应的人流密度为3.472人/m2,疏散速度为0.369m/s,约束条件;(5)-(6)表示疏散的开始两个阶段,即人员从听到疏散指令到第一个人员到达教室口然后再到下一层楼梯口的时间。
上述模型输入变量较多,且多为矩阵运算,可以用MATLAB软件进行编程求解。
4 算例分析
以某高校的主教学楼为例,已知共有6层楼,实测每个楼层的人数为pi,i=2,…,6每个楼层有三个楼梯,中间一个为主楼梯,宽度为Wi2=2.4 m,两侧为副楼梯,宽度分别为Wi1=1.2m, Wi3=1.2m,H=3.5m,L=6m,v1=2.01m/s,v2=0.6m/s,每層楼的平面图如图1所示。
我们取周一各楼层学生的上课人数,如表1所示。
将上述数据及给定的参数代入模型 ,用MATLAB编程计算得到的结果由表2给出。
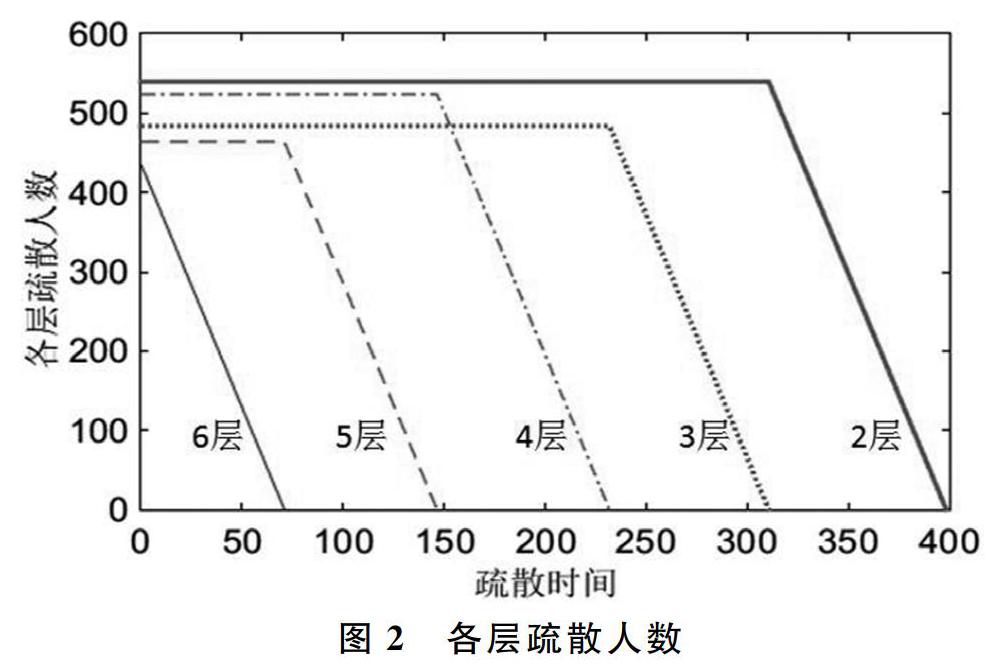
从上表中得出maxtj=398s,由(5)、(6)式求得tf=7.83 s,tl=3s,最短的总疏散时间为408.83s,各出口同时完成疏散,用时相同。而各层的疏散时间依次如图2所示。
从图2可见,从六层到二层疏散人数所用的时间依次增加,二层最大用时为408.83s,说明二层为关键路径,是整个教学楼疏散的必经之处,需要确保二楼楼梯的通畅,适当增大二楼楼梯的通行能力。并且该每层人员只有在上一层人员疏散完成之后,人数才开始减少,这说明底层需要疏散该层与以上所有的人员,越是底层,越要疏散更多的人员,所以可以考虑增大底层楼梯的通行能力。
上述的分析都是在楼梯的疏散能力为最大值的情况下,这需要学生在疏散时能做到完美的衔接与配合。而当疏散速度达到最大时,即人流密度为1.388人/m2,疏散速度为0.6m/s时,整个的疏散时间为577.43s。与最大能力相差168.6s,可见当疏散能力减少35%,疏散时间增加41.2%。而当疏散人数增加35%,疏散时间为548.6s,增加34%,说明如何合理应用楼梯非常重要。
5 结论
通过建立以总疏散时间最小为目标的疏散模型,本文发现楼梯疏散能力的大小是影响总体疏散时间的最大因素,尤其是较低的楼层。而楼梯疏散能力的大小又取决于人流的速度,人流密度和楼梯的宽度,所以基于上述三点提出几点优化方法与建议:
(1)需要对疏散时的人流速度与人流密度进行实地演练,让学生熟悉疏散路线与过程,做好人与人,楼层之间的衔接,提高楼梯的单位通量。
(2)需要对教学楼内的人数进行控制,不能超过最大通行能力下的最短疏散时间。
(3)教学楼下部几层可以与其他楼进行连接,以便增多疏散口,增大该楼层的疏散能力。
(4)对于楼梯口或楼门口要及时保持畅通,以免发生紧急情况时阻碍通行,减小疏散能力。
参考文献
[1]吕慧,杨玲,徐丹,屈楠.2017年校园设施安全事故统计分析与风险防控[J].安全,2019,40(01):50-53.
[2]张涛,吕淑然.大型教学楼紧急疏散仿真模拟研究[J].消防科学与技术,2015,34(06):747-749.
[3]赵宜宾,黄猛,张鹤翔.基于元胞自动机的多出口人员疏散模型的研究[J].系统工程学报,2012,27(04):439-445.
[4]王卫华,吴淑娴,程建.建筑物人员疏散方案的数学模型研究[J].武汉理工大学学报,2010,32(11):155-158+162.
[5]朱江,俞雪永,韩志科.高校教学楼内的人员紧急疏散数学模型[J].消防科学与技术,2008,(10):752-757.
[6]吕雷,程远平,王婕,高宇飞,刘静.对学校教学楼疏散人数及疏散速度的调查研究[J].安全,2006,(01):10-13.
