基于扇区复杂性数据的管制员工作负荷评估
2019-09-28许辰澄胡明华
许辰澄,赵 征,胡明华,江 斌,孔 航
(南京航空航天大学民航学院,南京 210016)
随着空中交通流量的不断增长与空域资源的日趋紧张,管制员工作负荷呈线性上升。据FAA 统计,在民航运输过程中出现的不安全事件约有21%与管制员工作负荷过载有直接关系,因此,对管制员工作负荷进行准确评估显得尤为重要。国内外专家学者对此也进行了较多研究。Cloarec 等[1]将各种定量工作负荷评价标准引入,结合扇区的交通态势建立了著名的RAMS 模型。Oktal 等[2]提出了管制员工作负荷预测模型,包括了监管任务、冲突探测与解脱、扇区之间飞机协调工作、航空器机动飞行等。Neal 等[3]选取了15 个扇区的复杂性数据指标,对管制员工作负荷进行了预测。国内学者对管制员工作负荷的研究主要分为以下两种:一是分析管制员陆空通话和操作行为,用数学公式计算管制员工作过程中消耗的时间,以此来量化管制员的工作负荷,如张明等[4]研究的DORATASK方法,刘继新等[5]结合计算机仿真技术来收集管制员行为的方法;二是分析管制员工作负荷值与各类扇区数据的关系,研究运行环境对管制员工作负荷的影响,建立基于扇区数据的管制员工作负荷预测模型,如吴丹[6]以终端管制扇区为研究范围,参考实际管制运行的情况,构建了基于扇区复杂性因素的管制员工作负荷线性和非线性回归模型,较为准确地预测了管制员的工作负荷。
综上,国内学者对管制员工作负荷的研究大多从客观数据出发,没有考虑管制员在管制过程中人的主观因素。在建立基于扇区复杂性数据的管制员工作负荷模型时,单纯回归模型的预测精度和稳定性不佳,神经网络、SVM 等机器学习模型又缺乏对扇区数据的可解释性。因此,将主观与客观相结合,先根据调查问卷和管制模拟实验得到具有主观成分的管制员工作负荷自评估值,引入客观的扇区复杂性数据,再通过因子分析、主成分分析及回归分析得到精度较高、解释性良好的管制员工作负荷评估模型。
1 扇区复杂性指标选择
Kopardekar 等[7]总结出管制扇区的82 个复杂性指标,包括:航空器数量、扇区高峰流量、到达扇区航空器数量、离开扇区航空器数量、爬升航空器数量、巡航航空器数量、下降航空器数量等。实际操作中由于人力、物力、资源的因素无法将上述82 个扇区复杂性指标全部进行统计、分析,最后结合实际管制经验及对一线管制员的调查问卷选出了13 个具有一定主观色彩的复杂性指标,并将其作为本次实验的自变量,如表1 所示。
2 管制运行模拟仿真实验的设计与实施
2.1 ATWIT 测评技术
管制员工作负荷输入技术(ATWIT,air traffic workload input technique)测评技术即空中交通负荷输入评定技术,是美国联邦航空局开发的基于界面的管制员工作负荷实时评定技术。该技术会让管制员在特定时间段内得到提示,将自己对管制工作中感受到的管制负荷进行主观评估。ATWIT 评估量级将管制员工作负荷等级从低到高分为1~10 个等级,被试管制员在实验中选取适当的数值来体现当时扇区交通情况对自身影响的强弱。表2 为ATWIT 测评标尺表。
实验前,管制员应熟知该测评标尺,并在雷达管制模拟实验中对自身感受到的工作负荷进行主观评估,并由一旁的实验人员进行记录。选取管制员自评的ATWIT 值作为因变量。
2.2 实验扇区环境
使用中国电子科技集团28 所开发的雷达管制模拟平台作为实践平台。管制场景选择为武汉天河机场进近管制扇区,扇区高度范围设定为0~5 400 m,进近区域管制员给飞机配备的高度范围为1 200~5 400 m(航空器在最后进近阶段低于1 200 m 移交给塔台管制),共15 个可选高度层。扇区由8 个边界点构成,分别为:A1(31.15′52″N 113.41′13″E)、A2(31.21′33″N 114.58′22″E)、A3(29.52′58″N 114.17′04″E)、HOK(31.19′32″N 114.05′20″E)、XSH(30.26′09″N 115.16′27″E)、WTM(30.38′14″N 113.08′27″E)、GUGAM(30.13′03″N 113.11′19″E)、LKO(29.54′10″N 114.41′29″E),其中HOK、XSH、WTM、LKO 为4 个进离场点。
具体的管制模拟界面如图1 所示。
2.3 实验任务
邀请20 位南京航空航天大学2013 级交通运输空中交通管理与签派专业的管制学员参与管制运行模拟实验。所有参与的管制学员均已参加了学院组织的模拟机培训,完成规定数量的雷达管制模拟培训,对于雷达管制指挥运行的通话用语和操作方法的熟悉程度较高。

表1 扇区复杂性指标及其含义Tab.1 Sector complexity index and meaning

表2 ATWIT 测评标尺表Tab.2 ATWIT evaluation scale

图1 管制模拟界面Tab.1 Simulated controlling interface
根据进近管制扇区的基本管制规则,实验要求管制员对扇区内航空器进行管制,通过发布改变飞行高度、航向和速度的指令使航空器之间保持安全间隔(水平间隔≥10 km,垂直间隔≥300 m,两者满足其一即为安全间隔),使移交进入扇区的航空器沿指定跑道延长线进近着陆,从扇区内离开的航空器以指定高度在指定航路点飞离扇区。
每次的实验时长为30 min,要求每位管制员尽力保证安全间隔,完成管制任务。同时,以3min 为一个时间片,共10 个时间片,辅助实验人员将按要求在模拟实验过程中和每个时间片节点上采集扇区数据和ATWIT值。具体的管制实验情景参数设置如表3 所示。
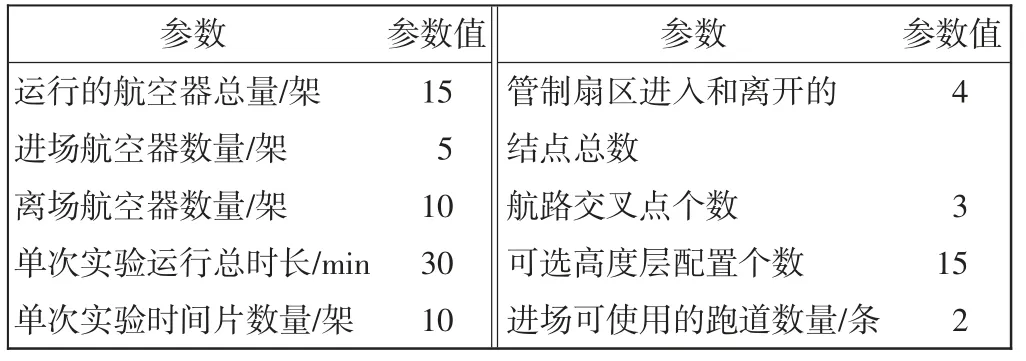
表3 管制实验情景参数设置表Tab.3 Parameter setting of experiment controlling scenario
3 主成分分析
3.1 概述
主成分分析的核心是利用降维的思想,将多个指标转化为若干个综合指标的线性组合。采用主成分分析方法主要是由于:①在建模过程中,扇区复杂性指标过多,使得建模难度较大;②有些扇区复杂性指标与工作负荷之间线性关系不明显,无法将这些变量与工作负荷进行线性组合;③在采集扇区复杂性指标过程中,发现一些指标之间有明显的相关性,这些变量之间信息的相关和重叠给建模带来困难,影响模型的精准度。通过分析变量之间的信息相关性,运用主成分分析的方法,不仅能够降低变量的维度,还能保证新主成分与工作负荷之间较强的相关性,也能消除新主成分之间的信息重叠性,适合与工作负荷进行回归分析。
3.2 基本原理
主成分分析的基本原理是因子分析。因子分析的本质是以最少信息丢失为前提,将众多原始变量整合成较少的几个因子,可用下面的数学模型来表示。
设有p 个原始变量x1,x2,…,xp且每个变量(或经标准化处理后)的均值为0,标准差为1。将每个原始变量用k(k <p)个因子f1,f2,…,fk的线性组合来表示,即

该因子分析的输出模型,也可用矩阵的形式表示
X=AF+ε
其中

由因子分析法概述可知x1,x2,…,xp之间是独立的,即

由此分析得到,因子分析的任务有两个:
1)确定式(1)中关于原始变量的表达式,即系数aij,εi(i=1,2,…,p;j=1,2,…,k);
2)确定因子与原始变量之间相关关系,得到能充分反映管制员工作负荷的影响指标。
3.3 基本步骤
3.3.1 因子载荷
式(1)中系数aij称为因子载荷,即第i 个变量在第j 个因子上的负荷,可用xi与fj间的协方差表示,即

由此可知,因子载荷aij作为变量xi与因子fj的相关系数,能够直观地反映第i 个变量与第j 个因子的关系的相关程度。因子载荷越大,该变量和因子的关系越密切。
3.3.2 因子特征值与贡献率
由上述计算得到的因子载荷,利用线性代数知识可计算出因子的特征值λk。
设第j 列元素平方和为

式中:gj2表示同一因子fj对各变量所提供的方差贡献总和。因子的方差贡献率越大,说明因子的重要性越高。因此,因子的方差贡献率是衡量每个因子相对重要性的尺度。
主成分分析把p 个原始变量x1,x2,…,xp总方差分解为p 个独立变量y1,y2,…,yp的方差之和,作为第k 个主成分yk的方差贡献率,即

一般地,从y1到yp的方差贡献率依次减小,综合初始变量的能力也依次减弱。
选取其中的m 个主成分来作为后续研究的新变量(m <p),则累积贡献率表示为

为使y1,y2,…,ym综合能力强,通常取m 使得累积贡献率达到一个理想的百分比,目的是求得新主成分中的变量,并验证其是否能够较好地代表原始变量。
3.4 扇区复杂性指标的主成分分析结果
根据指标分析的步骤可由SPSS 软件对实验中13个指标60 组数据进行相关系数分析,相关系数也称为因子载荷,分析结果如表4 所示。得到相关矩阵之后,可通过主成分分析得到主成分的特征值,再根据式(6)、式(7)可计算出扇区复杂性指标进行主成分分析之后新主成分的贡献率与累积贡献率。SPSS 软件运行结果如表5 所示。
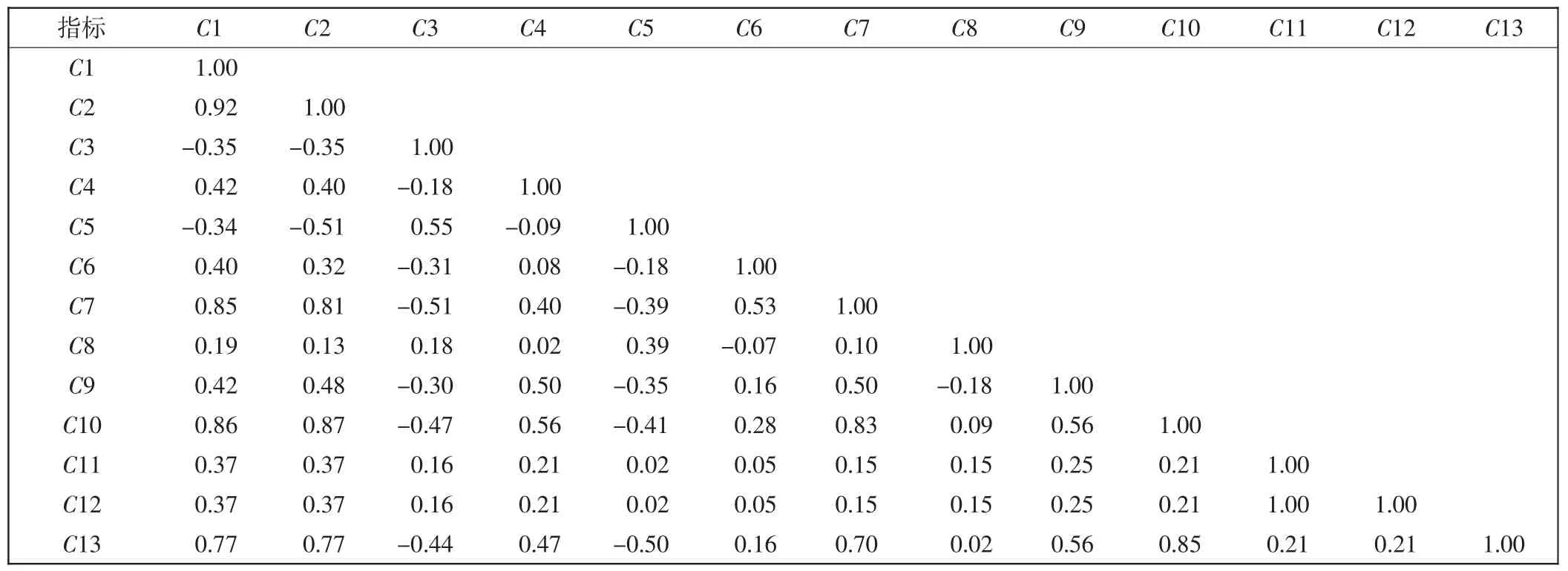
表4 扇区复杂性指标相关系数矩阵表Tab.4 Correlation coefficient matrix of sector complexity index
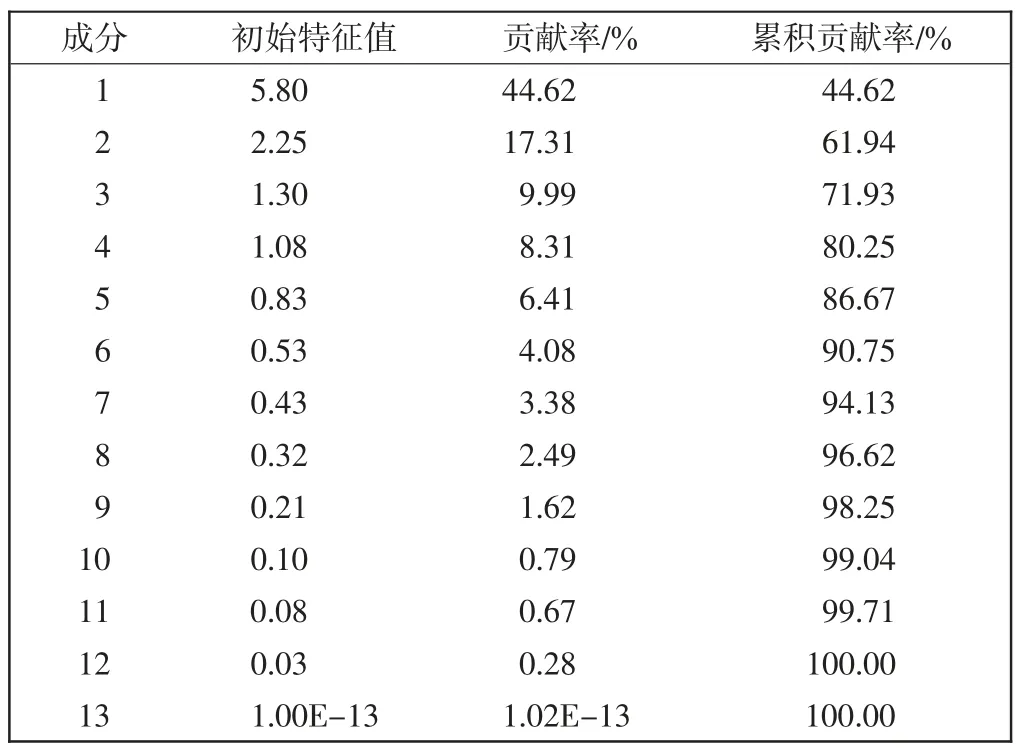
表5 特征值、贡献率及累积贡献率Tab.5 Eigenvalue,contribution rate,and cumulative contribution rate
为保证在提取主成分时原始变量所包含的信息丢失最少,提取特征值大于0.8 与累积贡献率大于85%的前几个主成分。因此,最终选取前5 个满足条件的主成分来代替原始变量进行后续的分析与计算。利用SPSS 软件可得到原13 个扇区复杂性指标在新主成分中所占比重,如表6 所示。
表6 列出了由原始变量分解出的主成分与对应变量的相关系数,继而依次计算特征向量矩阵,对变量进行主成分分析,如表7 所示。
据指标变量C1~C13 可形成主成分表达式为

参照Y1可以写出Y2~Y5的主成分表达式。

表6 成分相关系数矩阵表Tab.6 Correlation coefficient matrix of component
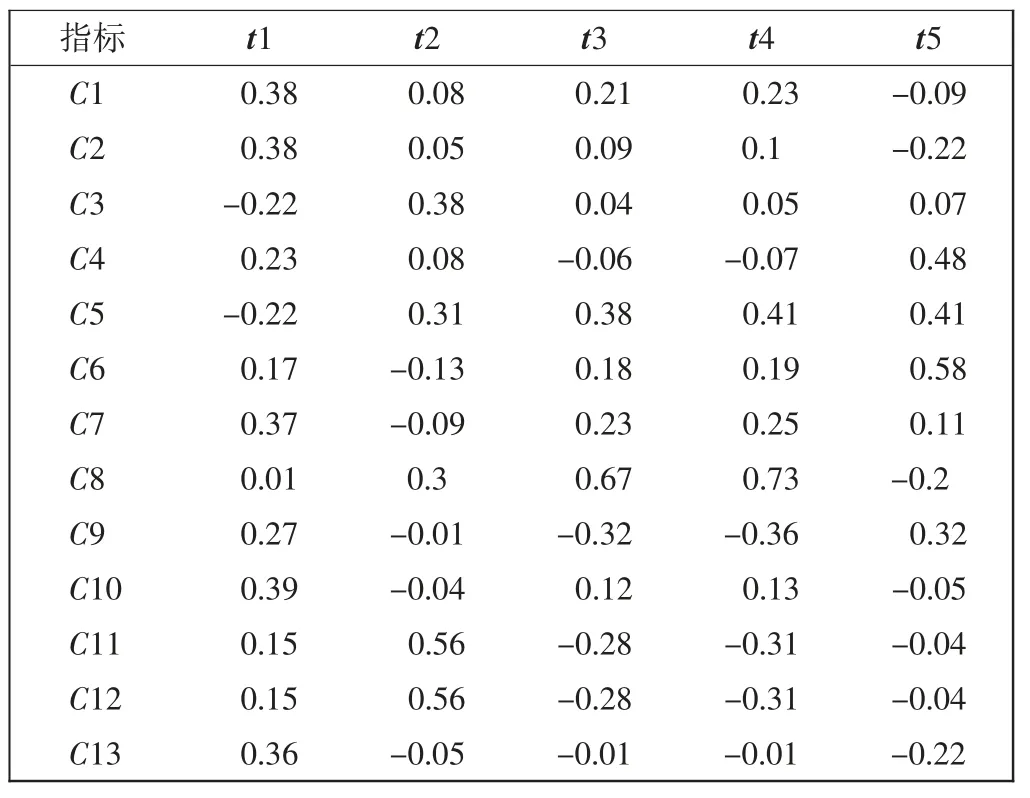
表7 特征向量矩阵Tab.7 Eigenvector matrix
4 管制员工作负荷回归模型
4.1 ATWIT 回归模型
将第3 节中求得的5 个新变量作为管制员工作负荷模型中的自变量,实验记录的ATWIT 值作为因变量来进行建模,并采用SPSS 软件进行拟合。
将统计出的60 组扇区指标数据进行回归分析,15 组数据用于验证模型的准确性。多元线性回归模型如下

其中:i 是第i 个时间片,i=1,2,…,10;φ 为某单位时间片内管制员ATWIT 值;Y 为某单位时间片内变量的值;e 为常量。
4.2 基于SPSS 求解回归模型
首先,将得到数据输入SPSS 软件中,得到ATWIT值与5 个新主成分变量的Sig(单侧)值均小于0.05,由此可得ATWIT 值与5 个变量间呈线性关系,且模型R2=0.854,反映出此时5 个自变量可解释因变量85.4%的信息,模型具有较好的精准度。由SPSS 软件求解出的因变量散点图如图2 所示。

图2 P-P 图Tab.2 P-P diagram
图2 中可看出,标准化残差呈正态分布,散点在直线上或紧靠直线,说明变量之间呈线性分布,满足建模的前提需要。因此,由SPSS 求得基于扇区复杂性指标的管制员负荷评估回归模型如下

通过式(10)能对管制员的工作负荷值进行评估,将15 组评估值与实际值进行比较,具体结果如表8所示。评估值与实际值之间残差的标准偏差为0.56,说明模型的评估值与实际值的离散程度较小,也说明模型具有较好的评估性能。
由表8 得出自评估值与实际值的走向情况,如图3 所示。
由表8 可得到模型计算出的残差绝对值最大为1.03,最小为0,考虑到ATWIT 评估法自身的主观性,可认为这样的结果具有实际的应用价值和一定的现实意义。从图3 折线走势上看,模型得到的评估值可较为准确地反映出当时管制员的工作负荷的大小,模型的准确性得到了有效验证。
4.3 评估模型对比
较现有的以扇区内航空器数量和管制过程中陆空通话的指令时间为研究对象的管制员工作负荷的评估模型,该方法具备一定的优势,具体表现在以下几个方面。
1)单纯计算管制员通话和操作时长的负荷评估方法没有考虑扇区的运行特征,将扇区复杂性数据加入模型有利于量化真实的交通态势,更加准确地评估管制员的工作负荷。

表8 负荷值的评估值与实际值对比Tab.8 Comparison between estimated and actual values of controller load

图3 评估值与实际值走向图Tab.3 Estimated and actual value trends
2)工作负荷是一种主观体验,通过直接测量陆空通话指令时间进行评估的扇区管制员工作负荷,虽然具有较强的客观性但忽略了人作为决策主体的主观感受。而使用主观评价法来对管制员工作负荷进行评估,在挑选扇区复杂性数据指标时引入了管制员的主观成分,因此其结果能有效地描述扇区管制员真实的工作负荷感受。
3)在传统的回归模型基础上引入了主成分分析,其评估结果有较高的准确性和良好的解释性,对于同一个扇区而言,只要采集到相应的扇区复杂性数据,就可快速评估出对应的工作负荷,也具有一定的实时性。
5 结语
将主观的管制员工作负荷值和客观的扇区复杂性数据相结合,提出了研究管制员工作负荷的新方法。采用因子分析与主成分分析法将客观的扇区指标进行降维,随后求得新变量与主观ATWIT 值之间的回归方程,并对此模型在实际运行环境中是否能较好地反映出管制员的工作负荷情况进行了验证,证明了这种评估方法的准确性、可解释性和实时性。
