基于信息增益和基尼不纯度的K近邻算法

孙 傲，赵礼峰

(南京邮电大学 理学院，江苏 南京 210023)

1 概 述

分类是数据挖掘领域的一个重点和热点方向。分类的方法众多，如决策树、K近邻算法、遗传算法、支持向量机、神经网络等。其中K近邻算法以其理论简单有效，且易于实现等优点在数据挖掘和机器学习领域被广泛应用。

K近邻算法的直观思想就是给定训练数据集，选择恰当的距离函数，通过已选的距离函数计算待分类样本和训练集中每个样本之间的距离，选取与待分类样本距离最小的k个样本作为待分类样本的k个最近邻，将待分类样本归为k个最近邻所属类别中的多数类。

K近邻算法虽然算法直观、简单有效，但是也存在着比较明显的缺点。首先k值的选择会直接影响分类的效果，k值较小易导致过拟合，此时待分类样本的类别判断只受与待分类样本较近的实例影响；k值较大易导致学习的近似误差增大，距离待分类样本较远的实例也会对分类结果产生影响。其次，K近邻算法在解决大规模数据分类时，分类速度较慢，其需要存储数据集中所有数据样本，计算待分类样本与数据集中所有样本之间的距离。另外，将每个属性等同看待，赋予相同权重，忽略了每个属性对分类的不同重要程度，影响了分类结果的准确性。

针对K近邻算法的不足，许多学者对其进行了研究和改进，逐渐完善了K近邻算法体系。针对k值选择影响分类结果的问题，路敦利等[1]将BP神经网络与kNN相结合，通过对训练样本使用k值不同的K近邻算法进行初步分类,同一数据会得到多个不同的初步分类结果集;然后将初步分类结果集作为BP神经网络的输入,再对BP神经网络进行训练分类。优化了传统K近邻算法精度受k值影响的问题，提高了分类准确率。孙可等[2]提出SA-KNN算法，优化传统K近邻k值选择问题，引入系数学习理论，通过局部保持投影LPP重构测试样本，利用l2,1范数去除噪声样本，寻找投影变换矩阵进而确定k值。豆增发等[3]提出一种根据最小距离个数来增长式地确定k值的方法，将待分类样本与所有训练样本的欧氏距离按大小排序，从最小距离开始，按距离大小等级得到m个k值选择序列，选择使样本正确分类的最小k值，作为K近邻的k值；同时运用信息增益确定属性重要程度，计算加权距离进行K近邻分类。

属性等同看待忽视了属性对分类的重要性，王增民等[4]根据信息熵理论，计算各分类属性与分类的相关性，剔除相关度低的样本，并依据保留特征的相关性作为权重，计算加权欧氏距离，选择K近邻，优化了距离度量。陈振洲等[5]提出FWKNN算法，将SVM算法应用到K近邻特征权重的度量中，以SVM算法中参数w作为特征的权重，并以此计算加权欧氏距离，选取k个近邻。

合适的距离度量函数影响分类效果，周靖等[6]将样本特征参数的熵值与样本分布概率的乘积作为特征对分类的相关度,并根据相关度值衡量特征对分类影响程度的强弱以定义样本间的距离函数，优化了在进行近邻选择时多数类别和高密度样本占优的情况。杨立等[7]提出SDKNN算法，分析属性内取值的语义差异，定义语义距离构成距离函数，优化了同一属性取值的语义差异所带来的影响。

分类速度随数据维度和样本量的增加急剧下降，余小鹏等[8]针对K近邻算法搜索慢的缺陷，提出自适应K最近邻算法，建立半径生长的BP神经网络模型，在以测试点为中心的超球内搜索，缩小了搜索范围，提高了搜索效率。江昆等[9]提出运用随机森林算法对变量进行排序，剔除不重要的变量，降低数据维数，提高K近邻算法在处理高维数据集的性能。Chen Yewang等[10]针对K近邻分类速度慢的问题，提出一种改进基于缓冲区的K最近邻查询算法，有效减少搜索待分类样本的时间复杂度。

不同的决策方式使k个近邻对待分类样本有不同的分类，杨金福等[11]在模板约简K近邻算法的基础上提出TWKNN算法，利用模板约简技术，将训练集中远离分类边界的样本去掉,同时按照各个近邻与待测样本的距离为k个近邻赋予不同的权值,增强了算法的鲁棒性。肖辉辉等[12]提出一种FCD-KNN算法，首先通过距离度量函数计算待分类样本与训练样本的距离值，通过距离值选择k个样本，定义类可信度函数，根据各类近邻样本点的平均距离及个数判断待测试样本的类别，优化了K近邻决策的方式。

但是，目前对于K近邻算法的改进和应用[13-17]，大多使用不加权的欧氏距离或单一指标的加权欧氏距离，无法全面准确地度量分类特征对分类的重要程度。针对这一问题，利用信息增益和基尼不纯度的综合指标确定分类属性的重要程度，只有信息增益足够大且基尼不纯度足够小的特征才是真正重要的特征，即用信息增益和基尼不纯度的差值作为衡量特征重要程度的依据，并根据此综合指标构造权重，计算加权欧氏距离，进行K近邻分类。

2 相关知识

2.1 K近邻算法

K近邻算法是一种基于实例的懒散算法，其思想就是选择距离度量函数，根据距离度量，找出与待分类样本距离最小的k个最近邻，通过多数表决等方式进行类别预测。

算法流程如下：

(1)选择距离度量函数，计算待分类样本与数据集中所有实例的距离值；

(2)在数据集实例中，找出与待分类样本距离度量值最小的k个实例点；

(3)根据与待分类样本距离度量值最小的k个实例点所属的类别，通过分类决策规则(如多数表决)，决定待分类样本的类别。

不同的距离度量方式，所选取的k个最近邻不同，从而最终待分类样本的类别判断也会不同。因此选取合适的距离度量方式，对提高K近邻分类的性能尤为重要。

2.2 信息增益及算法

信息增益表示在已知某特征的信息而使得类别的信息的不确定性减小的程度。若特征为A，训练数据集为D，则特征A对训练数据集D的信息增益为g(D,A)。

g(D,A)=H(D)-H(D|A)

(1)

其中，H(D)为集合D的经验熵，表示对数据集D进行分类的不确定性；H(D|A)为在特征A给定条件下数据集D的经验条件熵，表示在给定特征A给定条件下对数据集D进行分类的不确定性。

因此信息增益就表示在给定特征A而使得对数据集D进行分类的不确定性减少的程度，所以信息增益大的特征具有更强的分类能力，该特征对分类的重要程度更大。

信息增益的算法流程如下:

(1)计算数据集D的经验熵H(D)。

(2)

其中，|Ck|为属于类Ck的样本个数；|D|为样本容量。

(2)计算特征A对数据集D的经验条件熵H(D|A)。

(3)

其中，|Di|为根据特征A的取值将D划分的第i个子集的样本个数；|Dik|为子集Di中属于类Ck的样本个数。

(3)计算信息增益。

2.3 基尼不纯度

基尼不纯度表示集合的不确定性，基尼不纯度越大，集合的不确定性也就越大。若经过某特征对集合进行划分，使得划分后集合的不确定性减小，则该特征较重要。

在分类问题中，假设集合D有k个类，则集合D的基尼不纯度为：

(4)

其中，Ck是D中属于第k个类的样本子集；k是类的个数。

经过特征A划分后，集合D的基尼不纯度为：

(5)

其中，Di为集合D中属性A取值为i的样本子集。

3 基于信息增益和基尼不纯度综合指标的加权K近邻分类器构造方法

基于信息增益和基尼不纯度综合指标的加权K近邻分类器将信息增益和基尼不纯度两个指标结合起来评价属性的重要性，综合利用了信息增益和基尼指数的两个评价指标的优点，对属性重要性的评价更加全面。信息增益越大的特征重要程度越高，基尼不纯度越小的特征重要程度越高。由此出发，若一个特征基尼不纯度足够小且信息增益足够大即信息增益和基尼不纯度的差值越大，则表示该特征对分类越重要。

构造流程如下：

(1)将信息增益和基尼不纯度综合指标定义为GaGi，属性A的GaGi指标的计算公式为：

GaGi(A)=g(D,A)-Gini(D,A)

(6)

计算数据集每个属性的GaGi指标，信息增益越大，属性越重要；基尼不纯度越小，属性越重要。所以属性的综合指标GaGi的数值越大，该属性的重要程度越大。

(2)根据属性的GaGi指标值构造属性权重，训练数据集D共有n个属性，其中属性A的权重构造公式为：

(7)

(3)根据每个属性的权重，建立加权欧氏距离d，样本点x1,x2之间的加权欧氏距离为：

(8)

(4)计算待分类样本与所有训练样本的加权欧氏距离，对距离值进行排序。

(5)指定k值，选取与待分类样本最近邻的k个训练样本。

(6)依据多数表决决策规则，将k个最近邻样本所属类别中的多数类别作为待分类样本的类别。

4 仿真实验

4.1 实值仿真

利用Python3编程环境构造分类器，分别采用UCI数据库中的Iris和Wine两个数据集验证该算法的有效性。为保证有充足的数据集用于训练，采用留存交叉验证的方法对每个数据集随机选择20%的数据作为测试集，剩下的作为训练集。为更加准确地估计分类器的错误率，进行多次迭代求出平均错误率作为分类器的最终错误率。

数据集信息如表1所示。

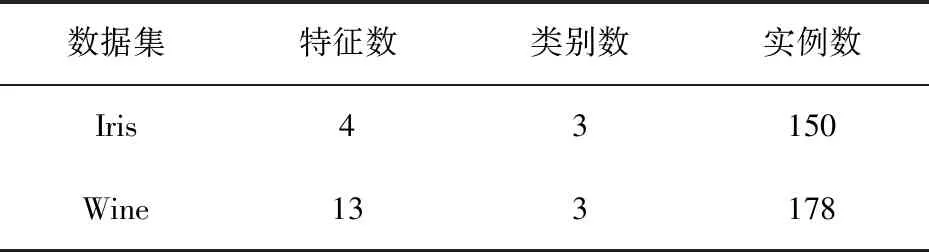
表1 数据集信息

4.1.1 Iris数据集仿真效果

该数据集包含150个实例和4个特征变量，特征变量分别为：花萼长度sepal length、花萼宽度sepal width、花瓣长度petal length、花瓣宽度petal width。

选取30个数据实例作为测试集，剩下120个数据实例作为训练集，用于构造加权分类器，同时为避免特征的数量值大小对样本间距离的影响，消除特征间数量值等级的差别，对数据集进行归一化处理。最后采用10次留存交叉验证法得到最终分类器错误率。

在不同k值下算法实现的平均错误率如表2所示。

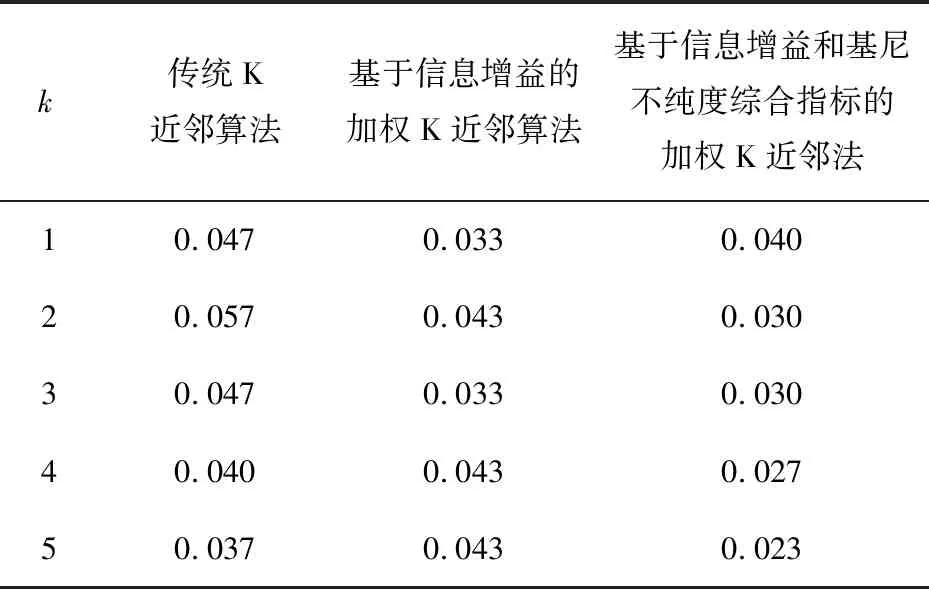
表2 不同k值下的三种算法错误率对比(Iris)

通过对比可以发现，加权K近邻算法总体优于传统K近邻算法，属性权重的度量方式和k值的选择不同也会影响分类精度，在此数据下，总的来说基于信息增益和基尼不纯度综合指标的加权K近邻法更优。

4.1.2 Wine数据集仿真效果

UCI数据库中Wine数据集包含178个数据实例，有13个红酒理化元素特征变量，对数据集进行归一化，随机选择35个数据实例作为测试集，剩下143个数据作为训练集，最后采用10次留存交叉验证法得到最终分类器错误率。

k值取1到5时，三种K近邻算法的平均错误率如表3所示。

通过对Wine数据集的算法仿真可以看出，基于信息增益和基尼不纯度综合指标的加权K近邻法最优，加权K近邻算法始终优于传统K近邻算法，在k等于1和5时分类器的准确度最高，分类效果最好。

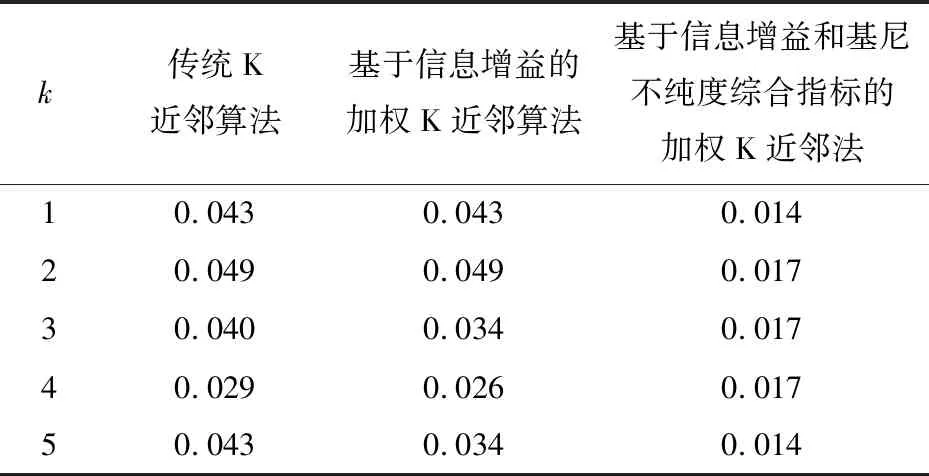
表3 不同k值下的三种算法错误率对比(Wine)

4.2 方法评价与不足

通过对两个真实数据集的仿真实验，可以得出区别对待属性特征，进行加权K近邻算法明显优于传统的K近邻方法；同时权重的构造指标也会对分类结果产生影响。实验证明，采用信息增益与基尼不纯度的综合指标比采用单一的信息增益指标划分属性重要程度更加合理，分类精度略优于采用单一的信息增益指标的K近邻法。

该算法也存在一定的不足，信息增益和基尼不纯度偏向于取值较多的特征。在特征取值较均衡时，算法具有很好的分类性能，在特征取值严重不均衡时，算法分类性能有所下降。

5 结束语

合理划分分类属性的重要程度，是数据挖掘分类问题和特征选取的重点方向。面对数据集的众多分类特征，如何选择合适指标评价特征变量的重要程度至关重要。针对传统K近邻算法将特征变量等同权重影响分类准确性和单一指标度量特征变量重要程度的不全面性的问题，提出一种基于信息增益和基尼不纯度的加权K近邻算法。该算法通过定义的GaGi指标对分类特征的重要程度进行度量，并以此为权重，计算加权欧氏距离，进行K近邻分类。对UCI数据库中Wine和Iris两个数据集的实验结果表明，该方法分类错误率比传统K近邻算法和基于信息增益的加权K近邻算法的错误率更低，分类性能更好。