两轮自平衡机器人控制系统设计

孙梦凡 桂文杰

（安徽工业大学电气与信息工程学院 安徽 马鞍山 243002）

0.引言

两轮机器人在近十几年得到了飞速发展，可广泛应用于战场侦察，紧急服务，智能轮椅[1]，邮件派送，危险物品的运输等等，其便捷、灵活、节能的特点不仅可以提供便捷服务，还可以降低人力成本提高工作效率。此外，两轮自平衡机器人集中运用了微电子，传感器，计算机，通信，人工智能，自动化控制等等这些技术，是典型的高新技术综合体[2]。其对保障交通安全，缓解交通拥挤，改善交通环境，完善未来智能交通系统也具有深远的意义，与传统轮式机器人相比，两轮自平衡机器人具有如下特点：

（1）机器人移动路径和方向更加灵活，容易控制，还可实现较小的移动范围，因此相比传统移动机器人应用领域更广泛。

（2）车体结构大大简化，为进一步实现新的功能提供空间，也适用于活动空间小或要求灵活运输的场合，例如步行街，广场，游乐会场等。

（3）平衡车驱动功率小，续航时间长，提出了环保轻型车的一种新模式[3]。

（4）相较于四轮车，平衡车的刹车系统更为灵敏和安全，车身比四轮车小很多，所产生的动能也相应小了很多。

虽然两轮机器人应用场合广泛，性能也较四轮机器人具有明显优势。然而如何维持机器人在复杂环境下的平衡和稳定一直是人们关注的问题，本文针对这一问题提出了一种两轮自平衡机器人控制系统。该系统以STM32F103C8T6 单片机为控制核心，整合分析MPU6050 采集的角度和加速度信息以及光电码盘采集的速信息来调整左右电机转速来维持机器人平衡。该系统不仅能在移动时维持平衡而且能够在一定干扰下自主调整姿态恢复平衡和稳定，同时具备在不同路径下自主循迹的功能，较好的满足了人们对机器人高稳定度和适应性强的要求。

1.系统总体控制方案

本系统总体分为两大模块：硬件设计模块、软件设计模块。硬件设计模块主要由STM32F103C8T6 单片机作为控制核心，MPU6050 传感器采集机器人的姿态，即机器人倾角θ 和角加速度X(t)，光电码盘检测机器人的速度，所有检测信息反馈给单片机后经分析计算控制调整左右电机转速以实现机器人平衡以及其他移动方式。在机器人维持平稳移动基础上模拟灰度传感器检测输出模拟信号AD 值，AD 值较大即检测白色区域，相反则黑色区域，根据黑色轨迹所在检测区域的位置调整机器人转向使之行驶回正确轨迹，实现循迹功能。软件设计模块主要分为三类控制设计：平衡控制、速度控制、方向控制，三者在控制运动过程中相互联系相互影响，其中平衡控制是基础，其他控制均在平衡控制的基础上实现。

所设计系统根据陀螺仪和光电码盘采集的数据结合卡尔曼滤波控制算法对机器人进行融合控制，实现机器人平稳运行以及其他移动方式。系统总体控制方案图如图1 所示。

图1 系统总体控制方案图

2.机器人硬件设计方案

为降低机器人的重心，使整个系统稳定性更高，系统采用对称布局的双层结构。如图2 是机器人的整体三维结构图。机身由亚克力板作为上底板，不锈钢板作为下底板，PCB 板搭在车底盘上，底盘前方安装四个模拟灰度传感器，底盘后方安装两个数字灰度传感器，中部放置驱动以及稳压装置，单片机主板等。

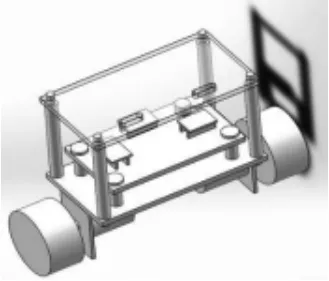
图2 机器人三维结构图

系统采用STM32F103C8T6 单片机作为控制核心，通过MPU6050传感器采集机器人的姿态，传感器采集的是机器人倾角θ 和角加速度X(t)，安装在两个电机上的光电码盘检测得到机器人的速度，检测信息反馈给单片机后经分析计算相应调整电机转速以实现机器人平衡以及其他移动方式。在机器人维持平稳移动基础上模拟灰度传感器检测输出模拟信号AD 值，机器人根据AD 值的大小来判断检测的是黑色区域还是白色区域，当检测到黑色轨迹在机器人正中位置，保持直线行驶；当黑色轨迹在机器人正中偏右（左）位置，左（右）轮电机比右（左）轮电机转速快，从而调整机器人位置使之行驶回正确轨迹，实现循迹功能。两轮自平衡机器人硬件控制系统如图3 所示。

图3 机器人硬件控制系统

2.1 电源模块

系统包含的电压有3.3V，5V，12V，其中整个系统包含的电源来源为12V 18650 锂电池，5V 电源由7805 稳压器提供[4]，作为传感器模块的供电电压，LM2596 稳压芯片提供3.3V 电源，作为单片机的供电电压。

2.2 电机及驱动模块

系统选用ASLONG JGA25-370 直流减速电机，这款电机可工作在6V 电压下，空载转速可达到77rpm，扭矩0.4，能够满足设计需要。驱动选用的是电机驱动器件TB6612FNG，该器件可以驱动两个电机，STBY 口接单片机的IO 口，清零电机全部停止，置1 通过AIN1、AIN2，BIN1,BIN2来控制正反转，VM接12V以内电源，VCC接5V电源，TB6612FNG 驱动电路图如图4所示。

图4 TB6612FNG 驱动电路图

2.3 灰度传感器

灰度传感器是模拟传感器，灰度传感器原理图如图5 所示，发光二极管作为光源与1k 电阻串联，照在检测物体上，1K 电阻起限流作用，光敏电阻与10K 电阻串联，光敏电阻具有光越强阻值越小的特性。当发光二极管照在白色物体上，白色物体反射所有光，亮度强，光敏电阻阻值小，分压小，输出的电压值高；当发光二极管照在黑色物体上，黑色物体吸收所有光，亮度弱，光敏电阻阻值大，分压大，输出的电压值低。单片机根据灰度传感器输出的高低电平分析控制左右电机转速实现机器人循迹。

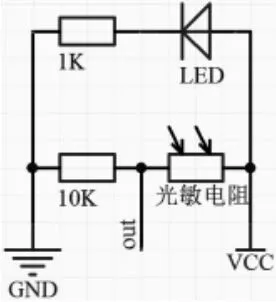
图5 灰度传感器原理图

2.4 MPU6050

MPU6050 作为机器人姿态测量模块是一种9 轴运动处理组件，由三轴陀螺仪和三轴加速度计组合而成，加速度计和陀螺仪用来计算机器人行进过程中实时角速度和加速度信息，用以保持车模稳定前进[5]工作电压为2.4V 至3.5V，其中陀螺仪和加速度计输出的模拟量经过三个16 位ADC 转化为数字量[6]，陀螺仪实质是角速度检测器，在机器人移动过程中单片机每隔一定时间读取陀螺仪的角速度，经计算得到当前车轮所在位置的角度θ。

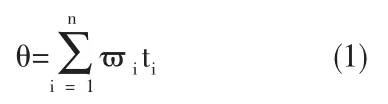
式中ϖi为第i 次陀螺检测的角速度，ti为第i 次陀螺仪检测的时间间隔，n 为一定时间检测的次数。由于陀螺仪运转一段时间以后，温度，白噪声，积分误差的累加导致的飘移现象等影响，积分并不能够得到完全准确的姿态，需要加速度传感器辅助校正，加速度计的低频特性好，可以测量低速的静态加速度，机器人根据加速度传感器测出的重力加速度在x,y,z 轴的分量与重力加速度的比值计算得到倾角α，单位弧度。

式中g 为重力加速度，gx为重力加速度沿x 轴分量，k 为比例系数。最后加速度计读出的角度和陀螺仪读出的角度经过卡尔曼滤波融合处理后，所得角度更加准确。

3.系统控制原理分析

系统的控制模块分为三个部分：平衡控制、方向控制、速度控制。其中平衡控制是其他控制的基础，所有的控制都是在平衡控制的基础上完成的。三者相互调节控制系统的三种运动状态即静止状态、直线运动、曲线运动。具体控制原理结构图如图6 所示。

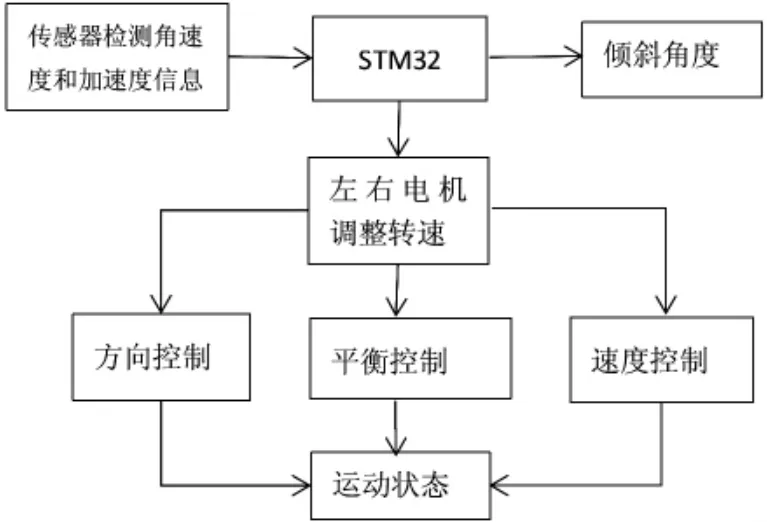
图6 系统控制原理图

3.1 平衡控制原理

实际控制中，传感器得到的角速度和加速度传回给处理器得到小车的倾斜角度，控制系统通过控制电机使两个车轮向车身倾斜的方向滚动，并相应调整转速产生扭矩力以维持动态平衡，宏观上表现为静止。这里通过一个外力干扰模拟机器人维持平衡的条件，假设外力干扰引起车模产生角加速度x(t)，如图7 所示，沿着垂直底盘方向进行受力分析，可以得到小车倾角与车轮加速度以及外力干扰加速度a(t)x(t)之间的方程如下：

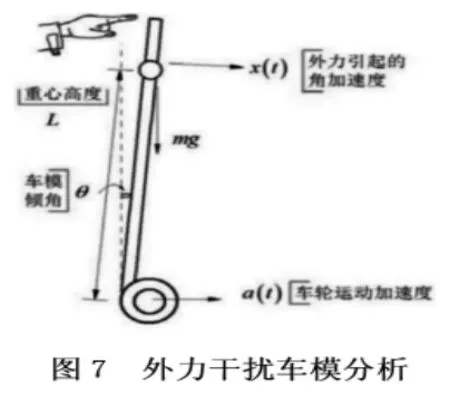
由以上公式分析得到，在精确检测机器人倾角θ，控制车轮加速度α 情况下，可以维持平衡，从而验证机器人具备一定的抗干扰能力。

3.2 速度控制原理

一般的四轮机器人速度控制机制是通过编码器采集脉冲信号，通过单片机正交解码之后解析成当前速度值，当前值对比设定值，通过pi算法更新速度误差，累计误差到一定数值之后清零，以控制轮子转速在设定范围内波动，为负反馈调节机制。对于两轮直立平衡机器人来说，速度控制在一定意义上是“正反馈控制”，速度环计算得出的量按比例缩小叠加到角度环上，宏观上为了保持平衡，车身会在设定范围内加速运动。

3.3 方向控制原理

车体方向控制主要通过控制两个车轮的速度差实现，由速度环可知，通过改变两边轮子的设定速度，车身为了保持平衡，宏观上会有转向的表现。车体左转向时，在在小车平衡的基础上控制右轮转速增加一定值，左轮转速减少一定值；相应的右转向时在小车平衡的基础上控制左轮转速增加一定值，右轮转速减少一定值。

3.4 状态分析

小车有静止、直线运动，曲线运动三种运动状态，机器人在维持自身平衡的基础上完成这三种状态的控制，通过改变角度设定值，会使车身在保持平衡的基础上，完成各种路径的运动。角度设定偏差越大，车身运动越快，变化也就越大。

(1)静止：若车身重心位于电机轴心线正上方，机器人宏观上将保持静止状态，但调控过程中单片机读取计算出的测量偏差的存在使得电机始终以微小的转速产生较小的扭矩力来维持小车的平衡。

(2)直线运动：在车身保持平衡基础上，给予“往前或往后一个方向的力”微观上表现为设定的零点改变，车身为了保持平衡会不停的往设定方向移动。机器人直线运动中的三种姿态如图8 所示。

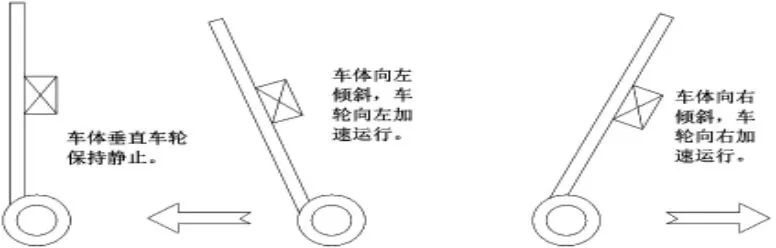
图8 机器人运动姿态

(3)曲线运动：在车身保持平衡的基础上，给予“左边或右边一个方向的力”微观上表现为设定差速运动，左右两轮设定的速度不一样，宏观上车身为了保持平衡会保持差速运动即曲线运动。

4.控制系统软件设计与实现

4.1 平衡控制算法概述

自平衡机器人平衡算法主要由速度环，转向环和角度环组成，速度环和转向环控制叠加在角度环上，由图像处理得到的偏差值叠加到速度设定值，由于车身在赛道上可能会左偏或者右偏，所以左轮右轮单独控制，两者基础设定值一致，根据跑道的不同情况，当前设定值会增大或者减小。根据当前的设定值和编码器读取的当前量，会得出速度环的偏差，写进速度pid 中，得到一个输出量，两轮的输出量根据跑道情况而有所改变。最终p 波输出的值为（速度环+转向环）*0.3+角度环*0.7.宏观表现为车身在姿态矫正的同时实现转向和直线加速。

用零点减去当前读取值乘上一个比例系数，归一化处理，得到两个新变量G_Now,a_offset。

具体代码如下：

Gyro_Now=(GYRO_VAL-gyro_z)*Gyro_ratio;//陀螺仪采集到的角速度归一化

angle_offset_vertical= (MMA7361_vertical-accle_z)*MMA7361_ratio;//加速度计归一化

最后对加速度计算值作限幅处理，控制在-90～90 范围内。

代码如下：

if(angle_offset_vertical>90)angle_offset_vertical=90;

if(angle_offset_vertical＜-90)angle_offset_vertical=-90;

得到两个变量后，使用卡尔曼滤波进行融合处理

float angle,angle_dot;

const float Q_angle=0.2,Q_gyro=0.1,R_angle=0.5, dt=0.005;

static floatP[2][2]={

{1,0},

{0,1}

};

static float Pdot[4]={0,0,0,0};

static const char C_0=1;

static float q_bias,angle_err,PCt_0,PCt_1,E,K_0,K_1,t_0,t_1;

void Kalman_Filter(float angle_m,floatgyro_m)//gyro_m:gyro_measure

{

angle+=(gyro_m-q_bias)*dt;

Pdot[0]=Q_angle-P[0][1]-P[1][0];

Pdot[1]=-P[1][1];

Pdot[2]=-P[1][1];

Pdot[3]=Q_gyro;

P[0][0]+=Pdot[0]*dt;

P[0][1]+=Pdot[1]*dt;

P[1][0]+=Pdot[2]*dt;

P[1][1]+=Pdot[3]*dt;

angle_err=angle_m-angle;

PCt_0=C_0*P[0][0];

PCt_1=C_0*P[1][0];

E=R_angle+C_0*PCt_0;

K_0=PCt_0/E;

K_1=PCt_1/E;

t_0=PCt_0;

t_1=C_0*P[0][1];

P[0][0]-=K_0*t_0;

P[0][1]-=K_0*t_1;

P[1][0]-=K_1*t_0;

P[1][1]-=K_1*t_1;

angle+=K_0*angle_err;

q_bias+=K_1*angle_err;

angle_dot=gyro_m-q_bias;

}

最后得到拟合角度和角速度的计算值。

最后输出p 波值speed_Start=angle*P_ANGLE+angle_dot*D_ANGLE;

4.2 速度控制

机器人速度控制是实现自平衡机器人平稳运行最重要的一步，它与机器人的方向控制，直立控制息息先相关[7]，与一般的控制不同的是，速度环是“正反馈”速度环计算出的误差乘以一个比例系数，按比例缩小，加进角度环，宏观表现车体为了保持平衡，向前或向后有加速现象。速度控制流框图如图9所示。

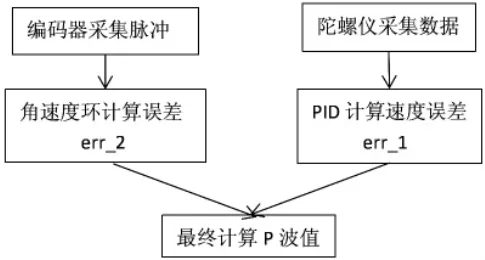
图9 速度控制框图

4.3 转向控制

转向环的控制是由摄像头采集计算一个向左或向右的偏差，加进角度环中，相应左右轮加速度或减速度，宏观表现车身为了保持平衡，有差速转向表现。由P*err+d*last_err 计算出的偏差是向左或向右，相应进行特殊处理。如果偏差向左，左轮速度期望值在原基础上增加转向所需量，右轮相应减少相应量。由于是双轮单独控制，会有两个独立的速度环，通过增加或减少预期值以达到让车子差速转向的宏观表现。转向控制的控制框图如图10所示。

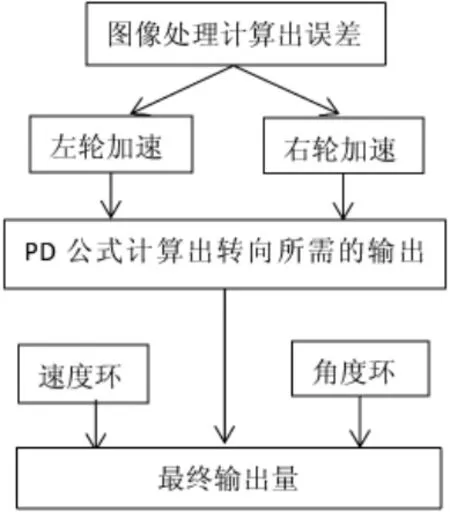
图10 转向控制框图

代码如下：

//$确定速度调节差值$//

speed_delta_thelast=speed_delta_last;

speed_delta_last=speed_delta_now;

speed_delta_now=expect_speed-speed_pulse;

//$速度闭环PID 调节$//

//速度 P_Adjust

pwm_delta_float_p=(speed_delta_now-speed_delta_last)*S_kp;

G_SpeedCtrl=G_SpeedCtrl+pwm_delta_float_p;

//速度 I_Adjust

pwm_delta_float_i=speed_delta_now*S_ki;

G_SpeedCtrl=G_SpeedCtrl+pwm_delta_float_i;

//速度 D_Adjust

pwm _delt a_float_d=(spee d_de lta_now-speed_delt a_las+sp eed_delta_thelast-speed_delta_last)*S_kd;

G_SpeedCtrl=G_SpeedCtrl+pwm_delta_float_d;

//电机输出值限幅

if(G_SpeedCtrl>3300)G_SpeedCtrl=3300;

else if(G_SpeedCtrl＜1000)G_SpeedCtrl=1000;

M1(G_SpeedCtrl);

M3(G_SpeedCtrl);

}

S_S=P*err+D*last_err;

If(err>0)

S_L=3000+S_S;

S_R=3000-S_S;

Else

S_L=3000-S_S;

S_R=3000+S_S;

If(err>0)

Speed_L=angle+（-abs（S_S）*0.1+abs(G_SpeedCtrl)*0.2）*P_ANGLE+angle_dot*D_ANGLE;

Speed_R=angle+（abs（S_S）*0.1+abs(G_SpeedCtrl)*0.2）*P_ANGLE+ angle_dot*D_ANGLE;

Else

Spee d_L=angle+（abs（S_S）*0.1+abs(G_SpeedCtrl)*0.2）*P_ANGLE+angle_dot*D_ANGLE;

Speed_R=angle+（-abs（S_S）*0.1+abs(G_SpeedCtrl)*0.2）*P_ANGLE+angle_dot*D_ANGLE;

4.4 控制系统软件总体设计

软件的主要功能有:系统初始化，传感器信号的采集、处理，速度检测，系统的运动状态控制即平衡控制、速度控制、方向控制[8]。三者之间相互联系，相互作用，三者关系图如图11 所示。具体工作过程和相互影响程度如下：

图11 系统总体控制关系图

(1)平衡控制：陀螺仪加速度计采集的当前角度，计算与设定角速度及加速度之间的偏差，输出相应大小的p 波。平衡控制受速度控制和转向控制的影响，速度环计算得出相应大小的p 波转换为对应的角度偏差，叠加到平衡控制中，形成加速现象。陀螺仪读取的三轴方向的加速度和角速度，计算融合成为欧拉角，通过欧拉角计算出转向所需的角度偏差。

(2)速度控制：编码器采集当前脉冲信号，反馈给单片机，与设定值相比，通过pid 矫正，将最终输出值稳定在当前信号。速度控制对转向控制的影响，当左右两轮速度设定值有偏差时，宏观上会有转向的现象；速度控制也会受直立控制的影响，最终输出值为直立控制计算出所需p 波大小加上速度控制设定大小融合而成。

(3)转向控制：由陀螺仪三轴方向的加速度和角速度六个值融合成欧拉角，转向所需设定值由欧拉角决定，叠加输出到速度环中，宏观上形成转向。

5.系统调试结果

测试一：姿态检测。机器人在正常移动时，机身倾角在0°附近变化，0°说明机身基本能维持直立。在人为施加一定外加干扰情况下，机身倾角以0 度为中心波动，且波动偏角越来越小，说明系统基本维持平衡，具备一定的抗干扰能力。

测试二：循迹检测。机器人在循迹过程中，机身距离中央黑线偏差在2cm 以内，人为改变机身偏角后，机器人自动调整转向沿原路径循迹，说明系统实现自主循迹，具有一定的适应性。

6.结语

两轮循迹机器人在研究平衡过程中采用模块化分析，分为三大模块：直立控制，速度控制，方向控制[9]，陀螺仪和光电码盘采集的数据结合卡尔曼滤波控制算法对机器人进行融合控制实现平稳移动，灰度传感器采集数值实现循迹，实验采集的数据均经过单片机分析机处理后控制左右电机转速实现机器人的功能。实际操作中，各功能模块相互协调并正常工作，循迹过程中机器人移动范围不超过2CM，适当干扰下，机器人能够自主调整并恢复平稳运行状态，实验结果表明所提出的的控制方案简单可靠，具有一定的实用价值。