基于聚类分析的月径流预测模型研究

周 娅,郭 萍,杨 柳,宋培培

(1.贵州省水利水电勘测设计研究院，贵州 贵阳 550002；2．中国农业大学 水利与土木工程学院，北京 100083)

岗南水库位于海河流域子牙河水系滹沱河中游，是滹沱河进入河北省后的第一个大型蓄水水库，水库位于河北省石家庄市平山县境内，始建于1958年，总库容15.71亿m3，与下游的黄壁庄水库共同保障石家庄的农业、工业、生活用水，同时通过联合调度保证了石家庄市和京广铁路的安全[1]。岗南水库的入库径流水量的多少关系着下游河北衡水、邢台、石家庄等地的工农业及生活用水，小觉水文站是山西省进入河北省的第一个水文测站，为流域两个大型水库之一岗南水库入库径流控制水文站，受水库调节作用较小，上游来水相对天然且资料条件较好，因此选取该代表站的径流进行预测分析对石家庄市可利用水资源优化分配规划具有重要的指导意义。在建立小觉水文站的月径流预测模型之前，采用灰色关联分析对小觉水文站月径流与各影响因子的关联度进行分析，提取出关联性较高的8个气象因子作为BP神经网络的输入；采用聚类分析法对1969—2009年小觉水文站月径流值进行分类，在此基础上采用BP神经网络对高流量和低流量分别进行预测模拟，结果表明，该方法可有效提高对数据序列中极值预测的精确度。

1 数据选择和资料来源

由中国气象科学数据共享服务网提供的五台山气象监测站和原平气象监测站1969—2009年的逐月气象资料，包括降水量、平均风速、平均气温、平均相对湿度、平均气压、日照时数、平均水汽压6个与径流形成相关的气象因子数据；由河北省水文水资源勘测局搜集到的1969—2009年小觉水文站蒸发量、降水量、月径流量数据，源自《海河流域子牙河水系水文资料年鉴》。在具体分析过程中，由于小觉水文站的蒸发量数据只能收集到2009年12月，为了使数据序列统一，进行建模的时候，所有的数据序列都采用1969—2009年的数据，未能同时反映2010—2013年的关联性，有可能影响模型的精度。

2 聚类分析法进行径流分类

人工神经网络预测多局限于建立单一构型的神经网络模型，采用此模型的输出过程常是一种估计各种数据情况的“最佳协调解”，其在拟合过程中试图兼顾全部数据的利益，目的在于降低总体误差，这种模型无法识别每个阶段径流量的主要影响因素并分别对待，因此无法使各个时期的径流模拟都取得较高精度的结果，如果将所有搜集到的数据放在一起进行训练得出的神经网络预测模型只能较好的模拟中等流量时间，而对极值情况，模型的性能则较差[2]。小觉水文站径流量年内变化大，5月多年平均径流量为5.66 m3/s，8月最高流量值达334.00 m3/s，每个时期的径流量值差别比较大，径流量主要集中在7—9月，具有明显的汛期和枯水期之分，夏季(7—9月)径流量主要由降水补给，春季主要由冰川融水补给，不同时期应考虑的影响因子也不同，故采用聚类分析法对1969—2009年月径流值进行分类，对高流量和低流量分别进行预测模拟。

2.1 聚类分析方法

聚类分析是依据研究对象的个体特征进行分类的方法，它能在没有先验知识的情况下，将一批样本数据按照性质上的亲疏关系进行分类，得到多种分类结果，每个分类内个体特征之间具有相似性，不同分类间个体差异性较大[3]。SPSS中的聚类分析方法主要包括系统聚类法和快速聚类法，无论是何种聚类方法，个体间的“亲疏程度”都将直接影响最终的聚类结果。对“亲疏程度”的测度一般有两方面：一是个体之间的相似程度；二是个体之间的差异程度，常采用距离来测度。聚类分析常用的距离包括定距型变量、定序型变量和二值变量，定距形变量包括欧氏距离(Euclidean distance )、平方欧氏距离(Squared Euclidean distance )、契比雪夫距离(chebychev)、Block距离、闵可夫斯基距离(Minkowski)、夹角余弦距离(Cosine)和用户自定义距离(Customized)；定序型变量包括卡方距离(Chi-Square measure)和Phi方距离(Phi-Square mearsure)；二值变量包括简单相关系数和雅克比系数[4]。聚类分析的步骤如图1所示。

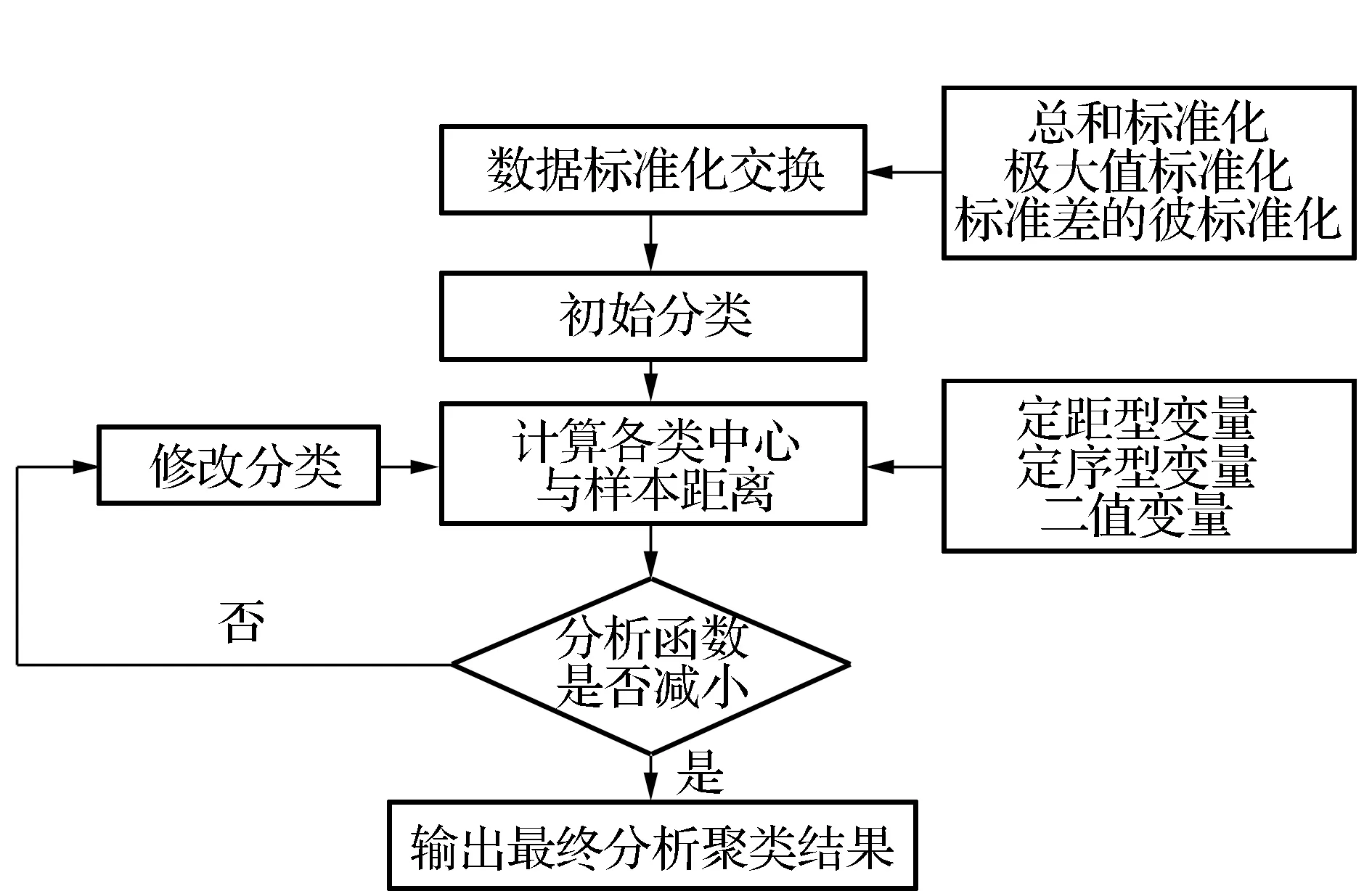
图1 聚类分析过程

本文中根据数据类型选择系统聚类法对1969—2009年多年平均月径流值进行分类，系统聚类法是目前使用最多的一种方法，其基本思想是首先把n个样本看成n类，然后规定样本之间的聚类和单个样本之间的距离，将距离最近的两类合为一个新类，在计算新类和其他类之间的距离，从中找出最近的两类继续进行合并，最后将所有的样品归为一类。该方法中常用的数据标准化方法包括标准化变换(Z Scores)，极差标准化变换(Range-1 to 1)，极差正规化变换(Range 0 to 1)，最大值为1(Maximum magnitude of 1)，标准差为1(Mean of 1)五种方法，本文中采用极差标准化变换先对数据进行标准化处理。

系统聚类中的聚类方法包括组内联接、组间联接、最远邻元素、最近邻元素、质心聚类、中位数聚类和Ward离差平方和距离法7种方法。大多数研究表明：综合特性最好的聚类方法为Ward最小方差法或类平均法，Ward最小方差法倾向于寻找观察数相同的类，类平均法偏向寻找等方差的类，本文中选择Ward离差平方和法进行聚类分析[3]。

2.2 分析结果

采用系统聚类法中Ward离差平方和距离法对1969—2009年多年平均月径流标准化值进行分类，结果如下：

从聚类分析树形图如图2所示，当聚成2类时，7—10月为一类，1—6月、11—12月为一类。该图展现了聚类分析中每一次类合并的情况，SPSS自动将各类间距离映射在0～25之间，并将聚类过程近似的表示在图上，本文接下来据此分类：7—10月为一类，1—6月、11—12月为一类对数据进行分组预测。

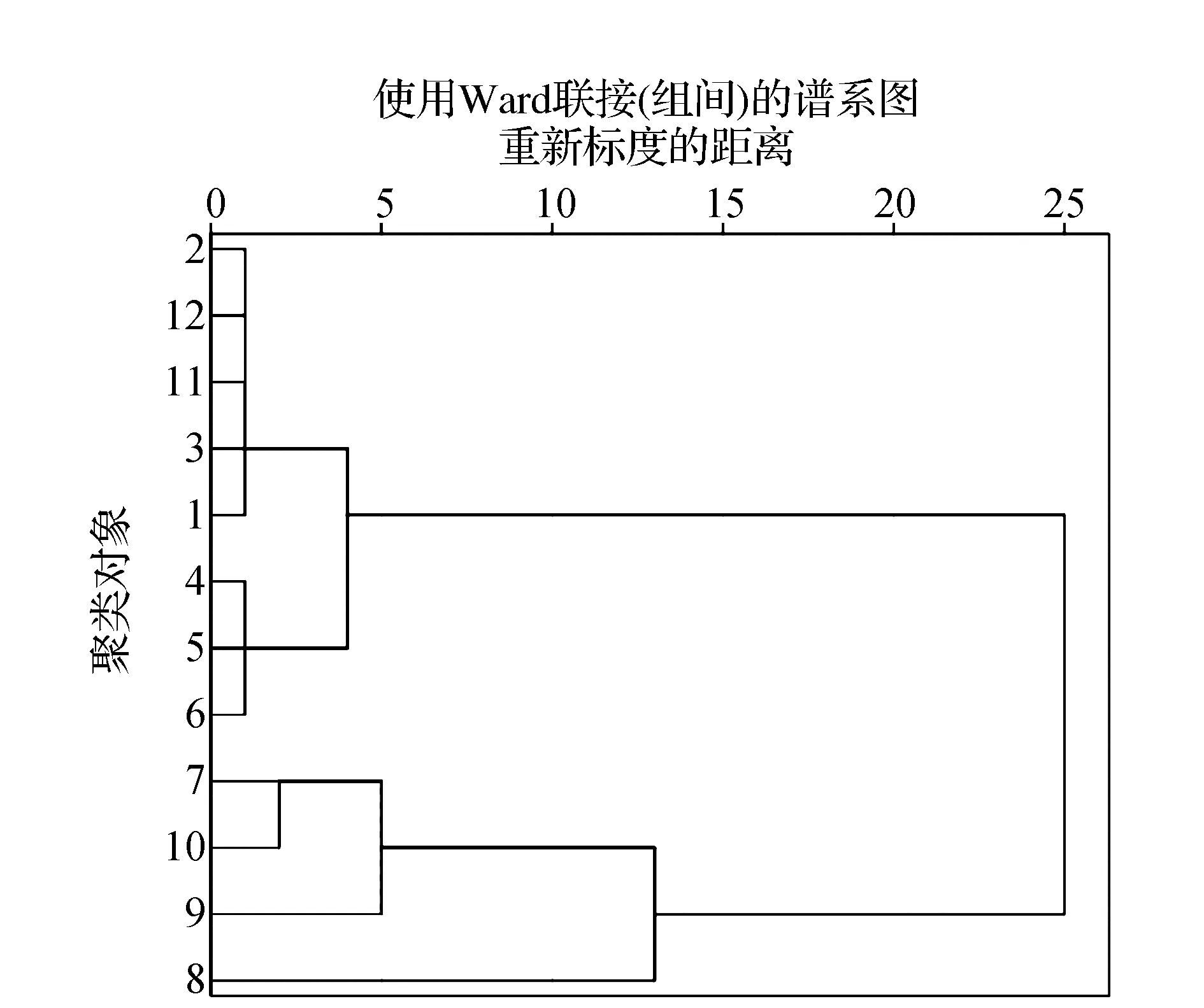
图2 系统聚类分析的树形图

3 月径流量影响因素分析

聚类分析将径流分为汛期(7—10月)和枯水期(1—6月、11—12月)两类，不同时期的径流量对应不同的影响因子，如降雨是汛期影响径流变化的主要因素，而在枯水期相邻水文站的流量则应为主要输入，需要采用灰色关联分析对不同时期月径流的影响因素做分析，确定每一时期神经网络的输入。

3.1 灰色关联分析方法

灰色关联分析的基本思想是根据曲线的相似程度来判断其间联系是否紧密，如果曲线越接近，曲线所代表的序列之间的关联度就越大，反之就越小。如若干序列{Xi(1),Xi(2),…,Xi(n)}，i=1,2,…,m(m为序列数)。如果将其看作一个一个“点”，他们都是变化的，而且点和点之间有联系；如果将他们看作是连续函数，那么点和点之间又缺乏信息。灰色系统理论中将这种缺乏信息的函数称为灰色序列[5]。而灰色关联分析的实质就是系统性的分析多个灰色关联离散函数之间接近度，将各个接近度进行排序，而这种接近度在灰色系统中，被称为灰色关联度。

灰色关联分析反映了离散序列空间的收敛和接近的程度，具有代数与几何双重特点。其对样本的要求不高，小样本也可以进行计算，离散序列可以是时间序列，也可以是非时间序列；同时可以对同一个样本进行多个参考序列的分析。这与单纯的回归分析相比，更具有整体性和层次性[5]。

径流形成是一个复杂的过程，各个影响因子之间的关系非常复杂，故采用灰色关联分析方法，对影响径流变化的因素进行分析。

3.2 分析结果

小觉水文站位于河北省石家庄市平山县小觉村，控制海河流域滹沱河(子牙河水系)上的岗南水库的入库径流，结合上面的分析，选取以下因子：x1五台山降水量、x2五台山风速，x3五台山气压、x4五台山气温、x5五台山相对湿度、x6五台山日照时数、x7五台山水汽压、x8原平降水量、x9原平风速、x10原平气压、x11原平气温、x12原平相对湿度、x13原平日照时数、x14原平水汽压、x15小觉水文站降水量、x16小觉水文站蒸发量作为影响小觉站径流量变化的因素。用DPS软件对这些影响因子进行灰色关联分析，分辨系数取为0.5，得到汛期和枯水期径流量和其他影响因子之间的关联度如表1和表2所示。

表1 汛期各影响因子与径流量的关联度

表2 枯水期各影响因子与径流量的关联度

从关联矩阵可以看出，汛期各影响因子与小觉水文站月径流的关联度排序如下：x15>x1>x5>x8>x12>x10>x9>x7>x14>x11>x4>x2>x6>x16>x13>x3，枯水期排序为：x9>x3>x5>x12>x15>x1>x2>x8>x13>x14>x7>x6>x16>x10>x11>x4，由1和表2可以看出，汛期各气象因子对小觉水文站月径流量的影响更大，相关系数均在0.8以上，属于高度相关，预测时将16个影响因子作为输入；枯水期各气象因子与小觉水文站月径流值关联系数较汛期低，其中x9、x3、x5、x12、x15、x1、x2、x8对应的灰关联系数在0.7以上，属于中度相关，其他因子与小觉水文站径流量的关联度不大，故选择前8个气象因子：x9原平风速、x3五台山气压、x5五台山相对湿度、x12原平相对湿度、x15小觉水文站降水量、x1五台山降水量、x2五台山风速、x8原平降水量作为神经网络训练的输入。

4 小觉水文站汛期月径流BP预测模型

前面通过聚类分析将小觉水文站径流量分为汛期和枯水期，汛期采用1969—2009年的7—10月的16个气象因子作为神经网络训练的输入，径流量值作为输出，采用MATLAB R2014a自带工具箱Time Series Neural Network(ntstool)建立汛期神经网络预测模型，采用的是能对数据量少、噪声大数据进行高精度模拟的Trainbr函数，网络结构输入层为17个神经元，隐含层为3个神经元，输出层为1个神经元。

图4个图分别表示：在测试期内观测值和预测值相关系数为0.8578，在测试期，观测值和预测值相关系数为0.8901，所有数据预测值和观测值的相关系数为0.8484，实测值和预测值吻合精度一般，但相关系数均显著的大于0.7，说明此模型也可以较好的模拟径流，从预测值和实测值对比如图5所示，模型在前120个月期间对峰值的模拟较好，但是对后40个月的模拟精度较差，这可能是因为在训练过程中训练期和测试期数据选择欠合理导致，但时间序列预测需要遵循时间规律进行，故无法将数据打乱进行预测，由此可见有必要对后40个月数据进行预测。

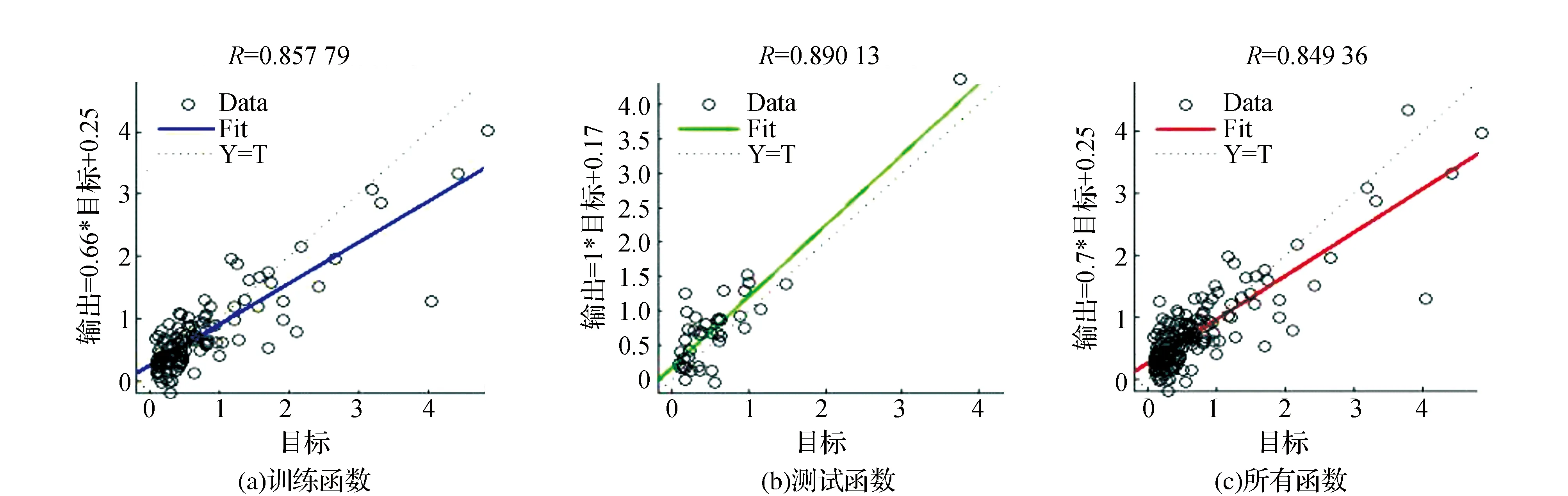
图3 汛期观测值和预测值回归分析图

图4 汛期各时期观测值和预测值对照图

5 小觉水文站枯水期月径流BP预测模型

由聚类分析结果得到：枯水期采用1969—2009年的11月至次年6月径流量值作为输出，与汛期不同的是，枯水期所选取灰关联分析得到的中度相关的原平风速、五台山气压、五台山相对湿度、原平相对湿度、小觉水文站降水量、五台山降水量、五台山风速、原平降水量作为输入进行预测模拟，同样采用MATLAB R2014a自带工具箱Time Series Neural Network建立汛期神经网络预测模型，选取Trainbr函数作为训练函数，网络结构输入层为9个神经元，隐含层为6个神经元，输出层为1个神经元。

图 6三个图分别表示：测试期内，观测值和预测值相关系数为0.8254，在测试期，观测值和预测值相关系数为0.800 89，所有函数预测值和观测值的相关系数为0.819 93，相关系数均显著的大于0.7，说明此模型也可以较好的模拟径流，从预测值和实测值对比如图所示，模型在前180个月期间对峰值的模拟较差，但是对后147个月的模拟精度在精度和变化趋势上均较好，主要是因为前180个月内径流量变化比较显著，而后147个月内径流量没有较高峰值的变化，模型体现了枯水期径流量峰值变化不大的特性，故对后期的径流量模拟较好，同时从前期灰色关联分析可以看出，选取的输入(气象因子)与输出(径流量)的灰色相关性一般，说明降水等气象因子对枯水期径流量影响不大，而与上游水文监测站得到的径流量值的相关性更大，而此部分数据的缺失也是预测精度不高的原因之一。

6 小 结

(1)本文针对小觉水文站径流量年内变化显著的特性，采用聚类分析法将数据按Ward离差平方和距离法分为两类：7—10月为汛期，11月至次年6月为枯水期；并在此分类的基础上对汛期和枯水期各气象因子进行灰色关联分析，选取灰色关联系数较大的气象因子作为输入：汛期16个气象因子与径流量的相关性均在0.8以上，故将16项气象因子均作为网络输入；枯水期气象因子与径流量的相关性在0.6～0.8之间，气象因子整体与径流量的相关性相对较低，选取相关性在0.7以上的8个气象因子作为网络输入；相关分析结果与实际中汛期易受降水等气象因子的影响、枯水期所受影响较低的情况相符。

(2)采用MATLAB R2014a中自带的BP神经网络预测工具箱ntstool进行预测，建立训练结果显示：汛期对峰值模拟较好，但对后40个月的预测模拟精度不高，这主要是因为预测中将上一时期的径流量值也作为输入进行训练，前期的径流量变化对后期的预测有影响，同时模型主要是对多数数据的趋势进行模拟，对突然在趋势上产生变化的数据响应差；

(3)枯水期则与汛期相反，模型对趋势的模拟较好，前180个月对峰值的模拟较差，在后147个月内径流量整体变化趋势减缓，模拟精度提高。

(4)由于在气象因子选取的过程中考虑滹沱河整个流域中五台山和原平两地的气象数据的影响，这在一定程度上反映了上游水文监测站径流量的变化，因此得到的模型也可以较好的模拟该时期的径流量。